
试卷代号:1024 座位号口 中央广播电视大学2006一2007学年度第一学期“开放本科”期末考试 计算机专业信号处理原理 试题 2007年1月 题 号 三 四 五 六 总 分 分 数 得 分 评卷人 一、是非题(每小题3分,共15分) 1.若偶信号f(t)的傅里叶变换为F(w),则F(t)的傅里叶变换结果一定为2πf(w)。 ) 2.平移,反褶,尺度变换,卷积是四种不同的信号运算。 ( 3.三角函数集,复指数函数集不是完备正交函数集。 ( ) 4.实偶信号的FT不是偶函数。 ( 5.单边指数序列的Z变换结果是常数。 ( ) 得 分 评卷人 二、单项选择题(每小题4分,共20分】 1.下列对于“信号”的说法,不正确的是()。 A.信号处理是对信号进行提取、变换、分析、综合等处理过程的统称 B.声音和图像都是信号 C.信号可以分为周期信号和非周期信号 D.所有数字信号处理涉及的步骤有2个:模数转换和数字信号处理DSP 2.f(t+3)*8(t一4)的计算结果是()。 A.f(t+1) B.f(t-1) C.f(t-9) D.f(t+9) 177
试卷代号:1024 座位号口口 中央广播电视大学200-T2a(?'7学年度第一学期“开放本科”期末考试 计算机专业 信号处理原理 试题 2007年 1月 题 号 二、 四 五 六 总 分 分 数 得 分 评卷人 一、是非题(每小题 3分,共 15分 ) 1.若偶信号 f(t)的傅里叶变换为 F(co),则 F<t)的傅里叶变换结果一定为 2nf(m)o ( 2.平移,反褶,尺度变换,卷积是四种不同的信号运算。 ( 3.三角函数集,复指数函数集不是完备正交函数集。 ( 4.实偶信号的FT不是偶函数。 ( 5.单边指数序列的 Z变换结果是常数。 ( 得 分 评卷人 二、单项选择题 (每小题 4分 ,共 20分 ) 1.下列对于“信号”的说法,不正确的是( )。 A、信号处理是对信号进行提取、变换、分析、综合等处理过程的统称 }3.声音和图像都是信号 C.信号可以分为周期信号和非周期信号 n.所有数字信号处理涉及的步骤有公个:模数转换和数字信号处理DSP 2. f(t-f-3),8(t-4)的计算结果是( )。 A. f(t-}-1) C. f(t一9) B. f(a一1) D. .}`'( t-i- 9 ) 177

3.下列关于傅立叶级数FS和傅立叶变换FT的说法错误的是()。 A.傅立叶级数和傅立叶变换的分析对象完全相同 B.信号在时域上周期离散,则其频谱也是周期离散的 C.信号在时域上周期连续,则其频谱一定是离散的 D.FT的线性性包括:齐次性和叠加性。 4.离散时间系统是指输人、输出都是( )的系统。 A.模拟信号 B.冲激信号 C.序列 D.矩形信号 5.Z[(-3)"u(n)]=()。 A. 3 B.2十3 C年3 D33 得分 评卷人 三、填空题(每小题4分,共24分) 1.[u(o)(t-Ddt= 2.FT与IFT具有 性,如果两个函数的FT或IFT相等,则这两个函数必然相 等,FT具有 ,如果$[f(t)]=F(w),则必有乎-[F(w)]= 3.信号时域平移不对其FT的 有影响,但是会影响到其 4.已知采样序列为x(n)=u(n一1)其之变换结果是 ,ROC为 1 5.已知X(x)= z(-1)ROC为2>1,则序列x(m)=」 6.序列x()为因果序列,其Z变换为X(x),x(n)向右平移2个单位后再Z变换,结果 Z[x(n-2)]= 178
3.下列关于傅立叶级数 FS和傅立叶变换FT的说法错误的是( ) A,傅立叶级数和傅立叶变换的分析对象完全相同 B.信号在时域上周期离散汉}J其频谱也是周期离散的 C.信号在时域上周期连续,则其频谱一定是离散的 D. FT的线性性包括 :齐次性和叠加性。 4.离散时间系统是指输人 、输出都是( )的系统 。 A.模拟信号 B.冲激信号 C.序列 D.矩形信号 5. Z[(一3)"u(n)]二( )。 z 2一 3 3 z-}-3 z z+ 3 3 z一 3 得 分 评卷人 三、填空题(每小题 4分 ,共 24分) i.)二u(t)8(t一‘’at- 2. FT与 I FT具有 性 ,如果两个函数的 FT或 I FT相等,则这两个 函数必然相 等 ,F I'具有 ,如果 } [ f(t) ]=F<w),则必有.}`-i [F(cu)]= 3.信号时域平移不对其 FT的 有影响 ,但是会影响到其 4.已知 采 样 序 列 为 x(}2) =u(n- 1)其 z变 换 结 果 是 ROC 为 5.已知 X(z)= 1 z<z一1)’ R(K 为 }刻}1,则序列 x(n)_ 6.序列 x(n)为因果序列,其 Z变换为X(z),x(n)向右平移 2个单位后再 Z变换,结果 1_[二(n一2)]= 178
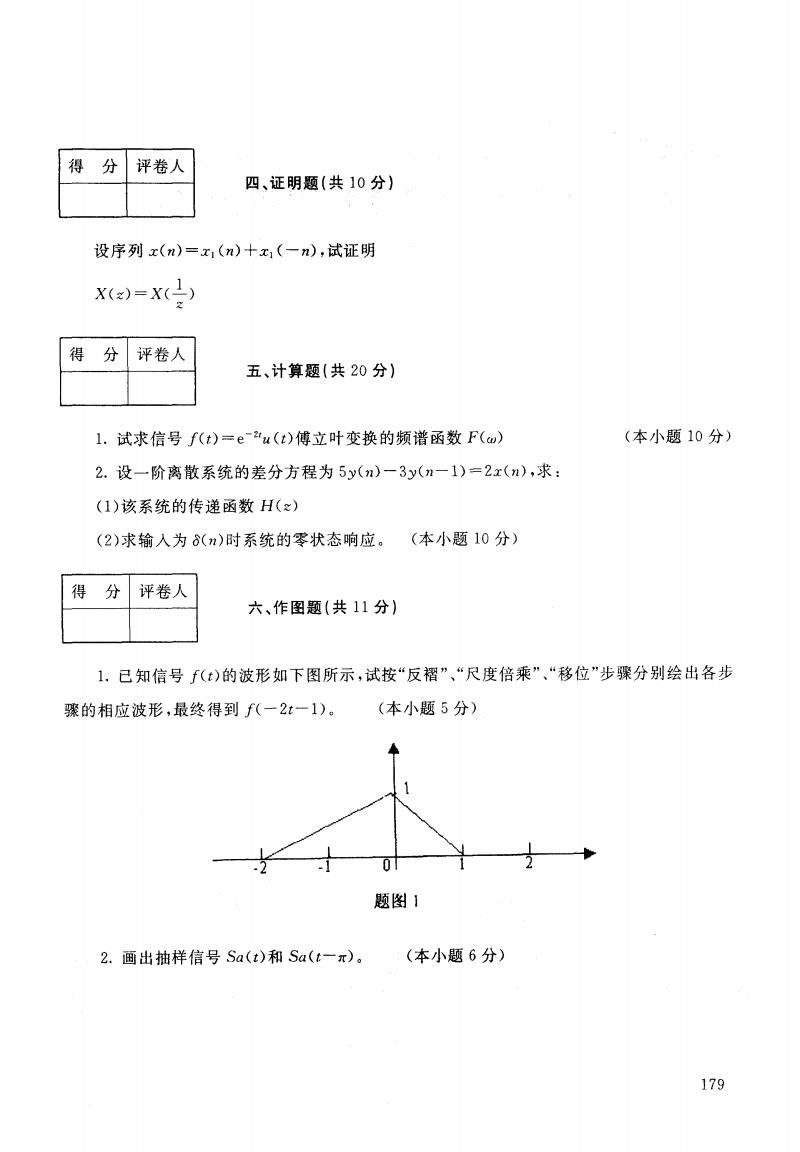
得分 评卷人 四、证明题(共10分】 设序列x(n)=x1(n)十x1(一n),试证明 x-x() 得 分 评卷人 五、计算题(共20分) 1.试求信号f(t)=e~u(t)傅立叶变换的频谱函数F(w) (本小题10分) 2.设一阶离散系统的差分方程为5y(n)一3y(n-1)=2x(n),求: (1)该系统的传递函数H(x) (2)求输入为(n)时系统的零状态响应。(本小题10分) 得 分 评卷人 六、作图题(共11分) 1.已知信号f(t)的波形如下图所示,试按“反褶”、“尺度倍乘”、“移位”步骤分别绘出各步 骤的相应波形,最终得到f(一2t一1)。 (本小题5分) 0 题图1 2.画出抽样信号Sa(t)和Sa(t一π)。 (本小题6分) 179
得 分 评卷人 四、证明题 (共 10分) 设序列 x(n)=x, (n)-f-xl (-n),试证明 X(:)一X(生) 得 分 评卷人 五、计算题 (共 20分) 1.试求信号 f(t)=e-2`u(t)傅立叶变换的频谱函数 F(}) 2.设一阶离散系统的差分方程为5抓n)-3扒n-1) =2x(n),求: (1)该系统 的传递函数 H(z) (2)求输人为 8(n)时系统的零状态响应 。 (本小题 10分) (本小题 10分) 得 分 评卷人 六、作图题 (共 n 分 ) 1.已知信号 f(t)的波形如下 图所示 骤的相应波形 ,最终得到 _f<-2t-1) a ,试按“反褶”、“尺度倍乘”、“移位”步骤分别绘出各步 (本小题 5分) // 题 图 2.画出抽样信号 Salt)和 Salt一二) (本小题 6分) 179

试卷代号:1024 中央广播电视大学2006一2007学年度第一学期“开放本科”期末考试 计算机专业信号处理原理 试题答案及评分标准 (供参考) 2007年1月 一、判断题(每小题3分,共15分) 1.正确 ,2.正确 3.错误 4,错误 5.错误 二、单项选择题(每小题4分,共20分) 1.D 2.B 3.A 4.C 5.C 三、填空题(每小题4分,共24分)} 1.1 2.唯一 可逆性 f(t) 3.幅度谱 相位谱 4马 1z|>1 5.u(n-2) 6.x-2X(x) 四、证明题(本题10分) 证明: 因为x(n)=x(一n),由Z变换的定义有 x)=x(mw(=之x(-0 (4分) 令k=一n,得: X)=r=x)=X) (6分) 180
试卷代号:1a24 中央广播电视大学Zoos--Zaa7学年度第一学期“开放本科”期末考试 计算机专业 信号处理原理 试题答案及评分标准 (供参考) 2007年 1月 一、判断题(每小题 3分,共 15分) 1.正确 2.正确 3.错误 4.错误 5.错误 二 、单项选择题(每小题 4分 ,共 20分 ) 1. U 2. B 3. A 三、填空题(每小题 4分,共 24分) l. 1 4. C 5. C .唯一 可逆性 f(t) .幅度谱 相位谱 Iz}>1 .u(},一2) .z一“X(z) 四、证明题 (本题 10分) 证明: 因为x(n)=x(-n),由Z变换的定义有 、,,1、 人 }- 少 , 、,1、_. 工、九少、— 少 、,1、__ xt一 刀少L— 少 (4分) 艺 于 一一 艺 ︸ 一- 令 k“一n,得 、,,1、 人 }- 少 牛 万 ,,、,1、‘ x}R夕l一 厂 手 z x(k)(z)-0= X (z) <6分) Ig}
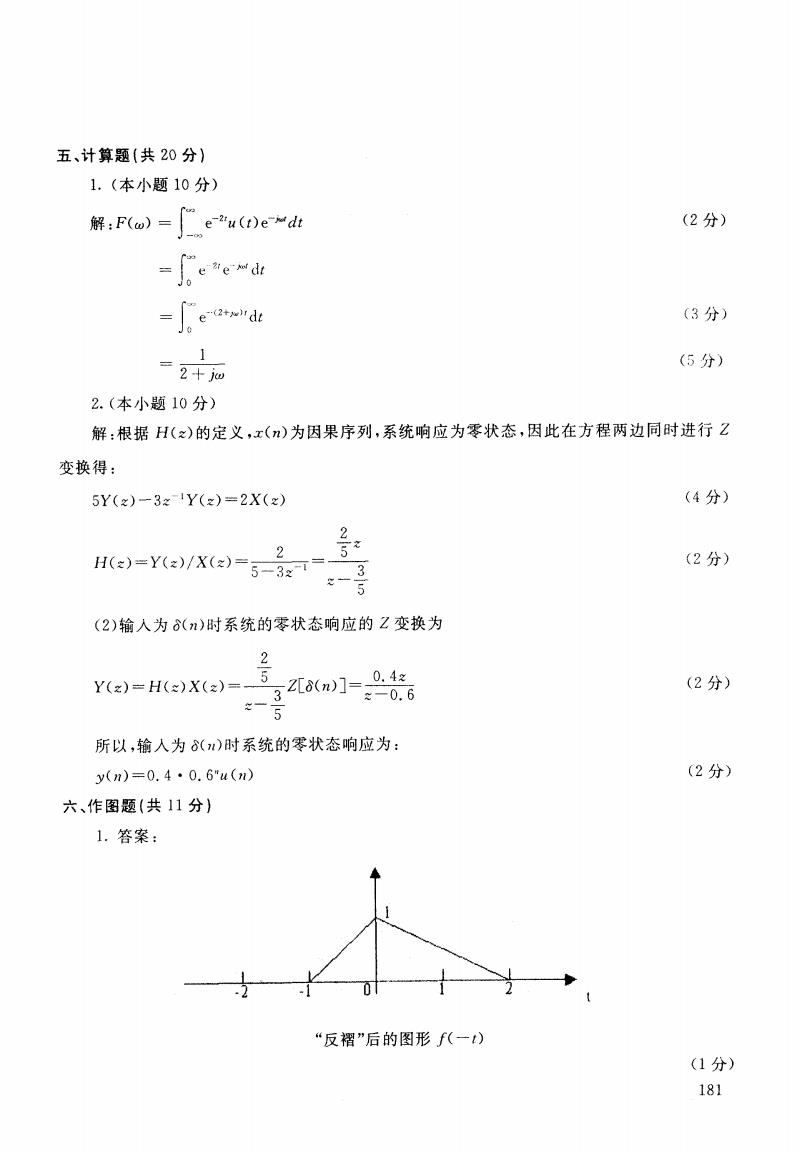
五、计算题(共20分)】 1.(本小题10分) 解:Fo)=Ceu(ee"d (2分) -eed vde (3分) 1 (5分) 2+j泗 2.(本小题10分) 解:根据H(x)的定义,x()为因果序列,系统响应为零状态,因此在方程两边同时进行Z 变换得: 5Y(x)-3x1Y(z)=2X(x) (4分) 2 2 H(e)=Y(e)/X(e)=5-3x= (2分) 3 (2)输人为6(n)时系统的零状态响应的Z变换为 2 Y)=He)Xe)=言320mw1=0.4 (2分) ≈-0.6 一 5 所以,输人为8()时系统的零状态响应为: y(n)=0.4·0.6"u(n) (2分) 六、作图题(共11分) 1.答案: “反褶”后的图形f(一t) (1分) 181
五、计算题(共 20分 ) 1.(本小题 10分) 解:F(田卜{二。一‘:,一dt (2分 ) 一}} 0e“‘ 、 ”“d‘ 一{一〕 ,eit (3分 ) 1 2+JW 2.(本/if、题 10分) 解 :根据 H(z)的定义 变换得 : (5分 ) ,x(n)为因果序列,系统响应为零状态 ,因此在方程两边同时进行 2 5Y(z)一3z一‘Y(z)=2X(z) (4分) 月(z)=Y(幼}X(幼 = 2 5一32.--1 2 }Jz (}分) 2一万 (2)输人为S(n)时系统的零状态响应的2变换为 2 ‘(二)一H<二,X(z,一击 Z[8<n)]- 5 0. 4z 2一0. 6 (2分) 所以,输人为 8( rc)时系统的零状态响应为: y(n)=0. 4·0. 6"u. (n) 六、作 图题 (共 n 分 ) l.答案: (2分 ) 一、\、 -一 寸- “反褶”后的图形 f(-t) (1分) 181

-1 “尺度倍乘”后的图形f(一2t) (2分) .2 2 “移位”后的图形f(一21一1) (2分) 2.答案: ◆Sai) 1 4 31 3元 (3分) 182
! 令 “尺度倍乘”后的图形 f<-Zt) (2分 ) __二_,止 _土 1 -一一 三---一一, “移位”后的图形‘f(-2t--1) (2分 ) 2.答案 : (3分) 182
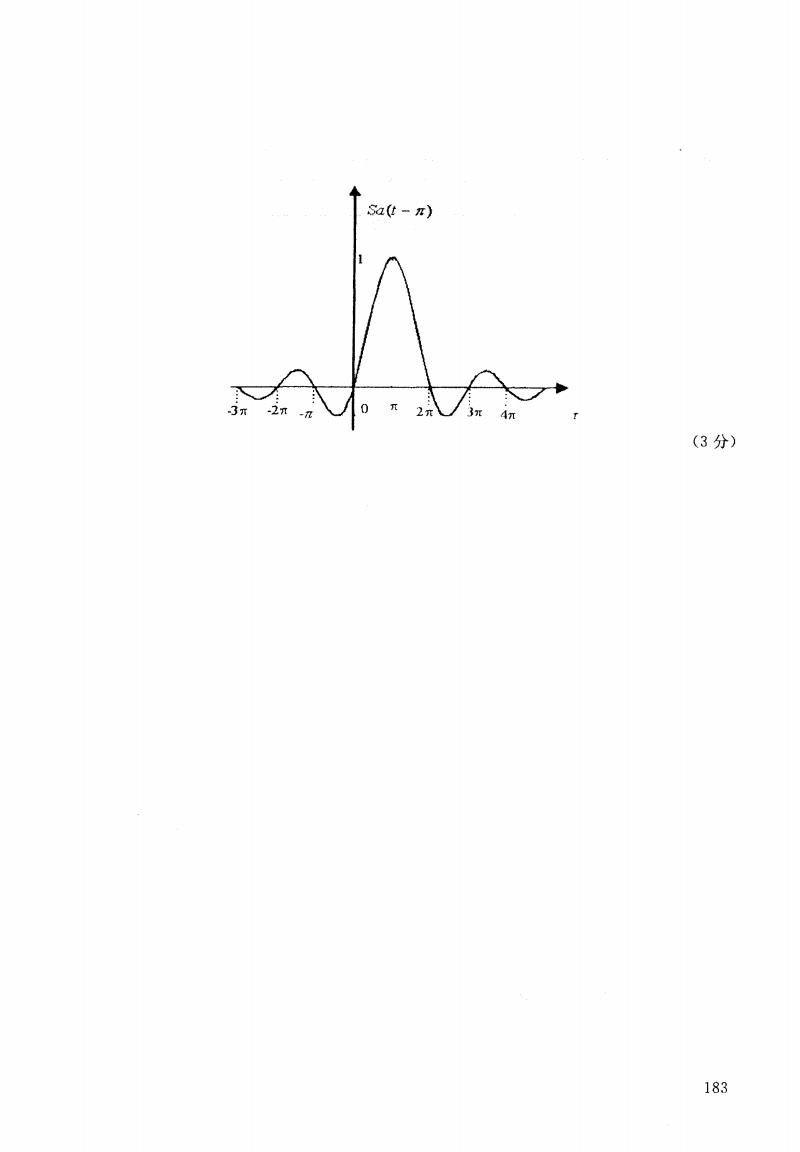
Sa(t-n) (3分) 183
(3分 )