
试卷代号:1002 座位号口 中央广播电视大学2006一2007学年度第一学期“开放本科”期末考试 计算机专业计算机数学基础(1)】 试题 2007年1月 题 号 二 三 四 总分 分 数 得分 评卷人 一、单项选择题(每小题4分,共20分) 1.下列各语句中是命题为( A.x+5<7 B.请把门关上! C.雪是黑色的 D.我正在说谎 2.下列不是重言蕴含式的为( A.A∧B→A B.AVB→A C.A,BAAB D.B→A+B 3.设集合A={1,2,3,4},A上的偏序关系R的关系图如图1,那么偏序集〈A,R)的哈斯 图是( A. B D. 4 02 20 图1
试卷代号:1002 座位号巨口 中央广播电视大学2006-2007学年度第一学期“开放本科”期末考试 计算机专业 计算机数学基础(1) 试题 2007年 1月 题 号 四 总 分 分 数 一、单项选择题(每小题 4分,共 20分) 3 图是 ( 下列各语句中是命题为( ). A.x斗5的哈斯 21 喊}4 2 _ 30 4 t 4_2’;

4.下列定义正确的是(). A,不含平行边和环的图称为简单图 B.不含平行边或环的图称为简单图 C.含平行边和环的图称为多重图 D.含平行边或环的图称为多重图 5.下列结论不正确是(). A.无向连通图G是欧拉图的充分必要条件是G不含奇数度结点 B.非平凡连通图G有欧拉通路的充分必要条件是G最多有两个奇数度结点 C.有向连通图D是欧拉图的充分必要条件是D的每个结点的人度等于出度 D.有向连通图D是有向欧拉图的充分必要条件是除两个结点外,每个结点的人度等 于出度 得分 评卷人 二、填空题(每小题4分,共20分)】 6.若集合AC0当且仅当 7.从130的整数中能被2或3除尽的整数的个数是一· 8.设集合A=(0,1,2),A上的二元关系R={(x,y》x,y∈AAx十y∈A},则R的关系 图为 9.设集合A={a,b,c},集合A上的二元关系R={(a,b),b,c),(a,c〉},S=《c,a〉,(c, c)},则R·S={ 10.无向完全图K?的所有非同构生成子图有个. 8
4。下列定义正确的是( ), A.不含平行边和环的图称为简单图 B.不含平行边或环的图称为简单图 C.含平行边和环的图称为多重图 D.含平行边或环的图称为多重图 5.下列结论不正确是( ). A.无向连通图 G是欧拉图的充分必要条件是 G不含奇数度结点 B.非平凡连通图G有欧拉通路的充分必要条件是G最多有两个奇数度结点 c.有向连通图D是欧拉图的充分必要条件是 U的每个结点的人度等于出度 D.有向连通图 D是有向欧拉图的充分必要条件是除两个结点外,每个结点的人度等 于出度 得 分 评卷人 二、填空题 (每小题 4分,共 20分) 6.若集合 A }-口 当且仅当 7.从 1 }- 3。的整数 中能被 2或 3除尽的整数的个数是 8.设集合 A=10,1,2),A上的二元关系R={(x,少 }二,yEA八x+y任A},则 R的关系 图为 9.设集合 A = {u,b,c},集合A上的二元关系R二{(u,b),(b,c),(u,c)},S = {(c,u),(c, ‘,>},则 R·S l0.无向完全图 K;,的所有非同构生成子图有 个
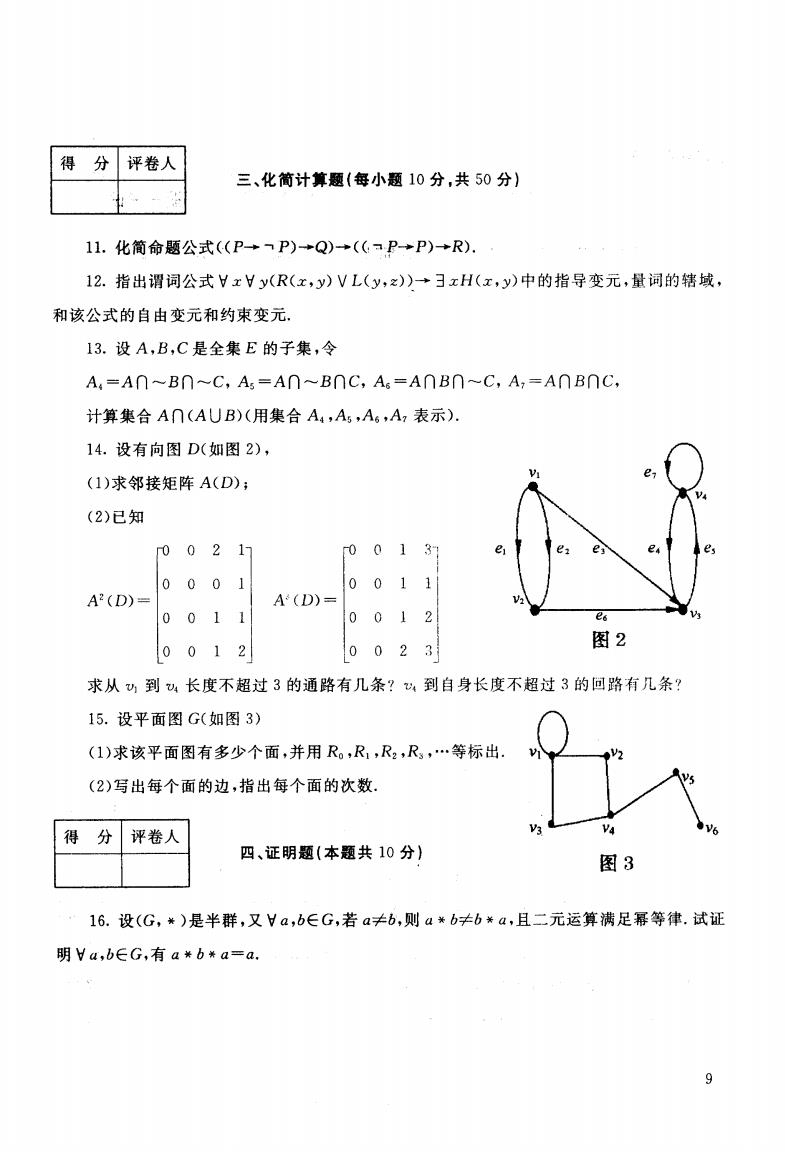
得 分 评卷人 三、化简计算题(每小题10分,共50分) 11.化简命题公式(P→P)→Q)→(P→P)→R), 12.指出谓词公式VxHy(R(x,y)VL(y,z)→3xH(x,y)中的指导变元,量词的辖域, 和该公式的自由变元和约束变元 13.设A,B,C是全集E的子集,令 A4=A∩~B∩~C,A=A∩~B∩C,A6=A∩B∩~C,A,=A∩B∩C, 计算集合A∩(AUB)(用集合A4,A5,A6,A,表示). 14.设有向图D(如图2), (1)求邻接矩阵A(D); e (2)已知 00217 0013 0 001 0011 A2(D)= A(D)= 0011 001 2 es 0012 0023 图2 求从少到4长度不超过3的通路有几条?到自身长度不超过3的回路有几条? 15.设平面图G(如图3) (1)求该平面图有多少个面,并用R。,R1,R2,R,…等标出. (2)写出每个面的边,指出每个面的次数. 得 分 评卷人 四、证明题(本题共10分】 图3 16.设(G,*)是半群,又Va,b∈G,若a≠b,则a*b≠ba,且二元运算满足幂等律.试证 明Ha,b∈G,有a*b*a=a. 9
得 分 评卷人 r 中 咋 盆 三、化简计算题《每小题 10分,共 50分) 11·化简命题公式(( P--},}')-'Q)一((。”」尸-,-P)}R). 12.指出谓词公式dx`d贝R(x,刃 V L(y,z))-} } xH(x,刃 中的指导变元,量词的辖域, 和该公式的自由变元和约束变元. 13.设 A,I3,C是全集 E的子集 ,令 A, =A门}B自一C, A, =A门一B门C, A6 =A门B门一C, A, =A门B门C, 计算集合 A(1(AUB)(用集合 A4,A},A6,A:表示). 14.设有向图 D(如图 2), (1)求邻接矩阵 A= A“(D)= 0 1 求从 二:到。4长度不超过 3的通路有几条?'}4到自身长度不超过 3的回路有几条? 15.设平面图 G(如图 }} (1)求该平面图有多少个面 ,并用 Ro,R1,RZ,R …等标 出. (2)写出每个面的边,指 出每个面的次数. 得 分 评卷人 四、证明题 (本题共 10分) 图 3 16,设(G,,)是半群,又ba,bEG,若 alb,则 “*b,-}b*a,且二元运算满足幂等律.试证 明b u,bEG,有 a,b*a=a

试卷代号:1002 中央广播电视大学2006一2007学年度第一学期“开放本科”期末考试 计算机专业计算机数学基础(1) 试题答案及评分标准 (供参考) 2007年1月 一、单项选择题(每小题4分,共20分) 1.C 2.B 3.C 4.A 5.D 二、填空题(每小题4分,共20分)》 6.A=0 7.20 02 图4 9.{b,a),(b,c>,(a,a〉,〈a,c)} 10.4 三、化简计算题(每小题10分,共50分) 11.((P+P)-+Q)→(P+P)→R) 台((PVP)→Q)→(PVP)→R) (2分) 台(PVQ)+(PVR) (4分) 台(P∧Q)V(PVR) (6分) 台(PAQ)VP)VR (8分) 台PVR (10分) 12.x,y是该公式的指导变元, (2分) 量词Yx的辖域是Hy(R(x,y)VL(y,z): (4分) 量词Hy的辖域是R(x,y)VL(y,z); (6分) 10
试卷代号:1002 中央广播电视大学2006-2007学年度第一学期“开放本科”期末考试 计算机专业 计算机数学基础(1) 试题答案及评分标准 (供参考) 2007年 1月 一、单项选择题(每小题 4分,共20分) 1. C 2.B 3. C 4. A 5. D 二、填空题(每小题 4分,共 20分) 6.A=必 7. 20 9.{(b,a),,P)-}Q)一 ((,P--}P)--}R) } ((,Pv ,P)-->G2)一 ((I'V P)-}R) } c} v Q>--}c,PvR) } c,pn ,Q> v(,pvR> }cc,p八,Q} v,P) V军 衬 ,尸VR 12. x, y是该公式的指导变元. 量词dx的辖域是d厂R(x,刃V L(y,z)); 量词 dy的辖域是 R (x,刃 V L(y,z); (2分) (4分) (6分) (8分) C10分) (2分) (4分) <6分 )

量词3x的辖域是H(x,y) (8分) 公式中的自由变元是之,y;约束变元是x,y. (10分) 13.A∩(AUB)=A∩(BU~B)∩(CU~C) (4分) =(AnB∩C)U(A∩~B∩C)U(A∩B∩~C)U(A∩~B∩~C) (8分) =A:UA:UAUA. (10分) 021 001 0 14.(1)A(D)= (5分) 000 001 (2)从1到w4长度不超过3的通路有4条,:到自身长度不超过3的回路6条.(10分) 15.(1)有3个面.分别记为R。,R1,R2,如图5. (3分) (2)R。的边为:(1,),(,),(,w),(4,),(,),(,5),(,山),(4,), (2,u), Ro R1的边为:(U1,U), Vi R2的边为:(1,h),(,4),(v4,2),(2,). (8分) R2 Vs deg(Ro)=9,deg(R1)=1,deg(R2)=4. (10分) V3 四、证明题(本题共10分)】 16.因为a,b∈G,若a≠b,则ab≠b*a,那么若a*b=b* 图5 a,则a=b (2分) 又*满足结合律,Ha,b∈G,有 (a¥b*a)¥a=(a¥b)米(a*a)=(a¥b)*a a*(a¥b*a)=(a*a)*(b¥a)=a¥(b*a)=(ab)*a (8分) 所以,(a*b0a)*a=a米(a¥b*a),故 u*b¥a=u 11
量词 3x的辖域是H (4分) =(A门B自C)U(A门一B门C>U(A门B门一C>U(A自一B门一C) (8分) =A, UA} UA} UA4 (is分) 月 卜. l sel es .e les.ees es J n ︺ 0 1 1 ,1 2 1 0 0 1 14.(1)A=<a*b),u u,(u*b*u)=(a}a),(b,a)=a*(b*u)= (u二b) * u (8分 ) 所以,(u *b}u) *u=u* (u*b*u),故 “关L关“二“ (10分) 11