
本章内容 第六章 s6-1 地下硐宝围岩 §62弹性理论计算巷道围岩与村砌应力 s6-3 巷道围岩应力分布的弹塑性力学分析法 应力计算及稳定性分析 s6-4 巷道围岩位移 6-5 围岩压力计筐 §6-6 巷道支护 $6-7竖井围岩应力计算及稳定性分析 本章的重点难点: 授课学时:12学时 1、圆形巷道围岩应力弹塑性理论分析方法: 2、围岩与支护相互作用原理 关键术语:围岩应力,围岩压力,弹性区,塑 3、弹塑性理论计算围岩压力 性区,松驰区,围岩变形压力,围岩松动压力, 4、块体平衡理论计算围岩压力: 围岩,普氏平衡拱,喷镭支护,稳定性。 5、压力拱理论计算围岩压力: 6、太沙基理论计算围岩压力 7、喷锚支护的力学作用: 8、圆形竖井围岩应力分布与稳定性评价。 要求 S6-1概述 1、掌握本课程重点难点内容: 、地下室的分类 2、掌握圆形巷道围岩应力分布规律 ty)是指人工开挖或天然存在于岩 3、了解椭圆形、矩形巷道周边应力分布 《库)、地下军事工程 交通道、水工隧道、地下厂房 4、誉想有内压圆形巷道图岩与村羽的应力计算 5、了解塑性区半径、松老区半径及围岩位移的计算公式 按闲壁受压情况:有压硐室、无压酮室 6、了解岩体构造对并壁稳定性的影响: 按断面形状:圈形、矩形、城门洞形、椭圆形 按与水平面关系:水平刚室、斜酮、垂直酮室(井) 7、掌握井壁压力的平面挡土墙计算方法: 8、了解并壁压力空心 按介质类型:岩石酮室、土丽 圆柱体挡土墙计算方法。 按应力情况:单式刚室、群刚
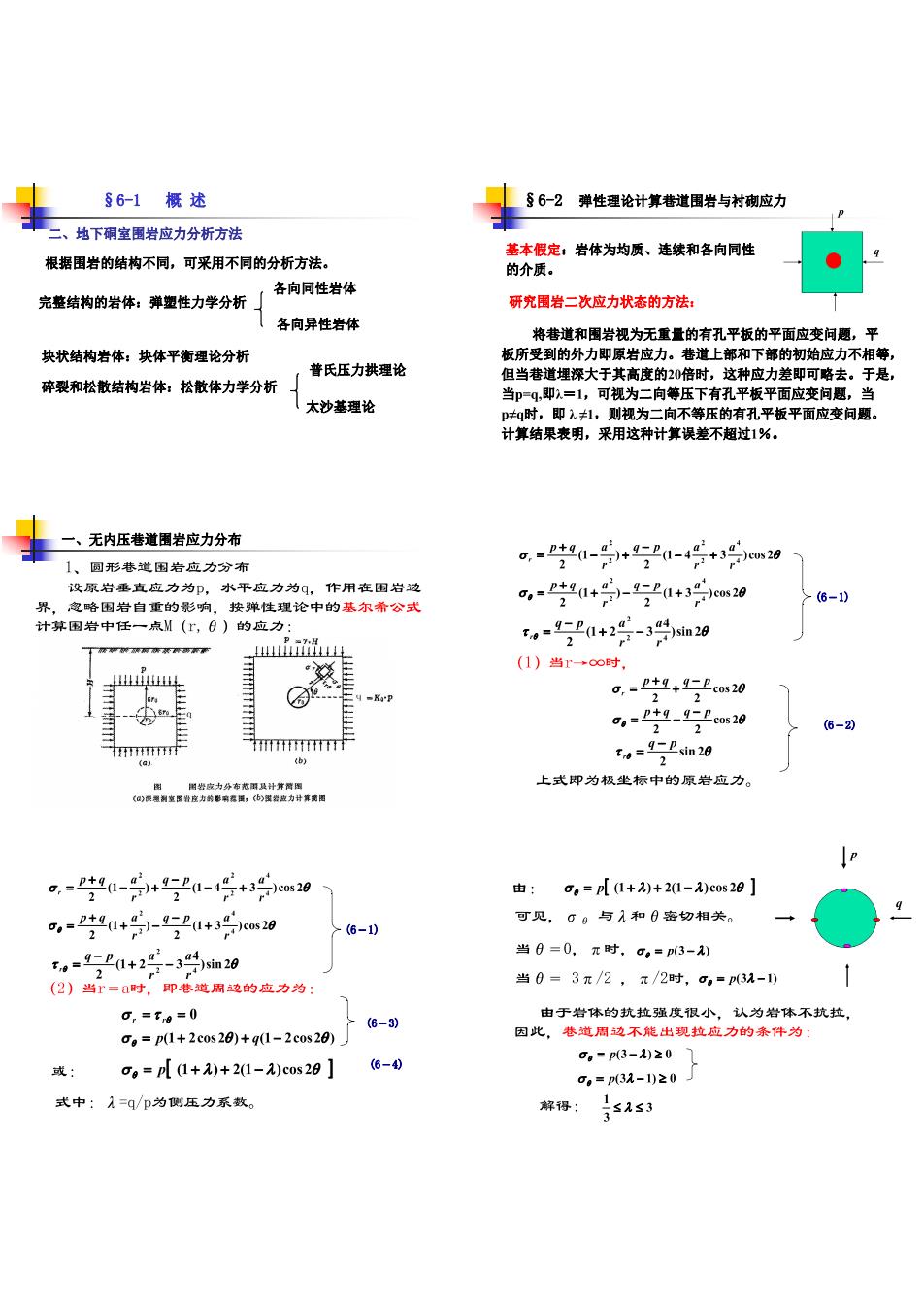
§6-1概述 主562鞋时水性与信方 二、地下碍室墨岩应力分析方法 根据围岩的结构不同,可采用不同的分析方法。 基本假定:岩体为均质、连续和各向同性 的介质。 完整结构的岩体:弹塑性力学分析」 各向同性岩体 研究围岩二次应力状态的方法: 各向异性岩体 将辖道和围岩视为无重量的有孔平板的平面应变问愿,平 块状结构岩体:央体平衡理论分析 普氏压力拱理论 板所受到的外 碎裂和松散结构岩体:松散体力学分析 但当巷道埋深大于 高度的 太沙基理论 时,即., 抑为 平板平面应变有。 计算结果表明,采用这种计算误差不超过1%。 一、无内压巷道围岩应力分布 1、回形毯道围岩应力分布 a,--54-4+w29 设佩岩垂直应力为,水平应力为( 作用在围岩边 g,=生41+-221+3cs20 6-1) 生理论中的尔滑公 =0+号-si0 (1)当r时, 6-2 hmmmmf T-9-Psin20 上式即为极坐标中的原岩应方。 o常经务力有天 -1-5+g-+3iow0 由:o。=l0+2)+21-)c0s20] o,-Pt"1+)-9P0+3os20 可见,G。与1和0密切相关。 >6-10 f。-9+2g-3sin28 当0=0,元时,,=3- (2)当=a时,即巷道周边的应力为: 当0=3π/2,元/2时,g。=3A-1) 由于岩体的轨拉强度很小,认为岩体不拉 6-3) 因此,巷道周边不能出现赖应力的杂件为 0。=3-)20 。=pl1+)+21-)cos28] 6-0 g,=p3-1)20 式中:1=q/p为侧压力系数

当0=0,π时,。=p3-) 不同的入下,巷道周边切向应力。的分布 当0=3元/2,x/2时,0。=3元-1) 不同的1下,卷域周边切向应力。。的分市: =0,n0=n/2,3/2 -p 11p a) 0 8D 2 50 20 2p 2.6 1/2 2.5p 0.5p (c) 1/3 2.67D Op 几种不同的入情况下圆形巷道周边应力分布 1/42.75p -0.25 不同的下,巷道周边切向应力G的分布 不网的入下,巷道周边切向应力G。的分布 几种不同的入情况下围形巷道周边应力分布 a防g2的7 a,=41-g)+1-4号+3gcm20 ,=p1- ,-生+-+3号cm0 6-10 o,=1+g)》 ,+号-学0 Fe=0 当r=,巷道周边应力为 (3)当p=4,即无=1时, 可见,0。、g月0元 ,t。=0 g,=1-) g。=2p (6-60) 类,1=1(轴对泰)时 当r·时,巷道原应力为: a,=1+)广8- 对圆形巷道国岩瘦力分有 展有刺。 ,=pg=pw=06-刀 o=0 圆形巷道开挖应力扰动觉围为巷道米径的3一5暗

主,久养程彩达空力分中 ,nta825 在单向应力作用下,椭圆形巷 道周边任 是向应习 若者B=0,pw=p,则: g,=0,Tg=0 若B=900,p4=p,则: -n22g y轴上的半b与轴上的半轴a的比值,即m=b/a: 车路p、p作用下由四 日洞壁上任意一点M与椭圆形中心的连线与轴的夹角。 B赛瘦作用线与转的突角: ,=p+mjcos0-1+ +m'si20-m2」 P 6-8 2+ ,=lem+2jc20-he+2m+m20-mmg cos'6 6- 道周边两中痕处(日=0,元)向应力为: 上式也可表示为: m-川+品-a]+g- ,-a+2m'0-ne2t4g"0-mw'0 卷道周地重底枫中燕处(日=3π/2,元/2)切向应力为 oa=l1+2m)z-1]-pl1+2-1] 0,=te=0 着(@)=(),即g1=2则可得: 的g 由(c)可得: 去⅓时能活形统比与队的关系 长轴。长抽方向原岩应力 6-助 短轴短釉方向原岩应力 1:s1:41312 应力相等,周边应力分布比较均幻。 可见,在原岩应力(如,1p)一定的素件下,g 轴比m而变化。为了获得合罐的应力分布,可通过调整 当,板中的。,出现应力,在=V4缘件下,应1 夏底板中点的应力为1,,出现切南应力相等
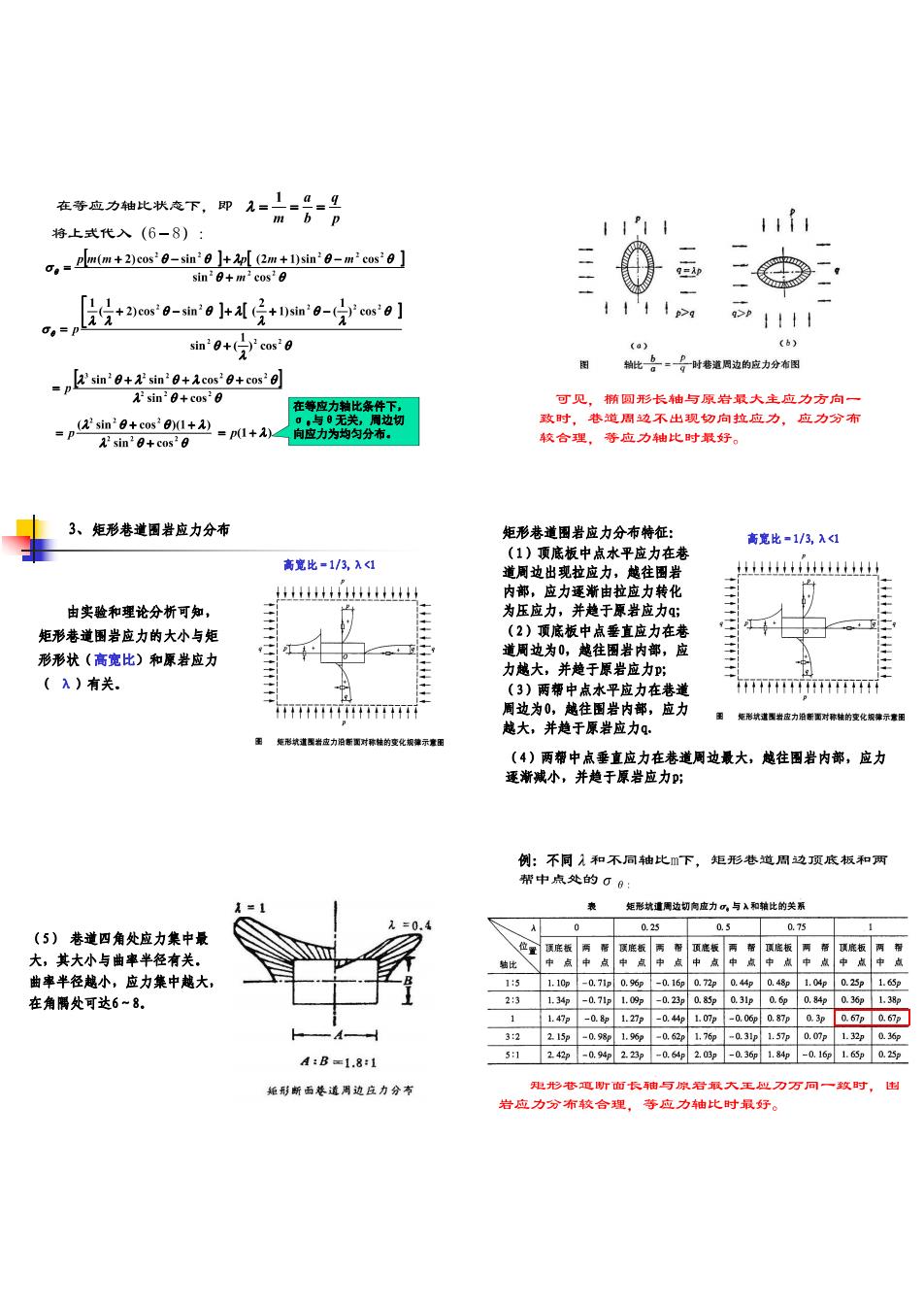
将上式代入(6-8): 11f1 o,.ltm+2m'0-h0+242m+sng-ms0 sin0+m2cos' ,· 2宝分+2os0-n0+利分+im0-分ew0】 sh'g+分'cos20 sincosc 可见,精圆形长与原岩最大主应力方向 =p2n0+emO+L=A+ 应力,应力分清 3、矩形巷道围普应力分布 矩形巷道围者应力分布特征: 高宽比■1/3入4 造项 t址女 内都,应为速渐由拉应 由实验和理论分桥可知, 为压应力,并楚于原岩应力 矩形巷道图署应力的大小与矩 点直应 形形状(高宽比)和原署应力 力越大,并于原岩应为 (入)有关. (3)两帮中点水平应力在巷道 “带7 (4)两帮中底垂直应力在卷道周边最大,越往圈岩内部,应力 逐渐戒小,并趋于原岩应力; :不同入和不同袖比下,短形巷道周边顶底板和两 (5)卷道四角处应力集中 其为 曲率半径越小 应力集 在角处可达68 5:14-422y-0.642y-031.4w-0116p02p 施形断西巷道周边良力分带 刀万同一时,由

4、巷道围岩分布的共同特点: (1)无论巷道断面形状如何,周边附近应力集中系数最 大,远离周边,应力集中程度逐渐减小,在距卷道中心为加3 边容哥出现拉应力,转角处 5倍巷道半径处,围岩应力趋近于与原岩应力相等。 道的稳定。 (④)巷道影响区随巷道半轻的增大而增大,相应地应力 (2)巷道围岩应力受侧应力系数入、巷道断面轴 中区也非道半轻增大而增大如果应力根高,在周边近过 说宋 省大 力超过岩体承较能力而产生的破裂区半径也将较大。 假定巷道边圈艺 出现拉应力 底板 的 点和两帮中 作用,巷道周边往往不是应力集中区,而是应力降低区,此区 域又叫嫌破松动区。该区城的范围一般在0.5左右。 二、有内压卷道围岩与村商的应力计算 主水灯健鞋中内区您活省对应的 1、内压引起的围岩附加应力 将速道围岩香成厚壁简,内径头 (1)厚壁简应力公式 广的 径为R 的理 -+二 墨和密肉有加后力计有 -+ 信-)厚壁筒应力公式 r2R2+r1) (8-9)厚壁简应力公式 得出在距中心为处的径向应力和切向应力为: a, ,=- (6-10 在距中心为r处的径向应力和切向应力为 a, =- (6-10 (3)原岩应力为p(从=1小、水工豫道中内压为p时的围岩应力: =0 a,=gn+ml- 上式即是内压p1引起的附加应力, =-n++ 在r=a(洞周边):O,=P: =-P ,e=0 t=0

2、有内压巷道围岩与衬纳的应力计算 2、有内压巷道围岩与村瘦的应力计算 (1)无裂豫围岩 ".1+[0-4,-40,】 A、刚度系数法求村砌的应力 将拉密公式代入得: 村南外周边的径向 位移 =0+xP0-2a2 设混凝士村脚港道日 内径为,外 为士 和漫凝士村内距道中心为 处的径向位移为,由弹性理论有: 当一时,即得村南外周边的位移 共-t[0-40,-40.】 ".42-n】 E 式中:t与ar 当时,衬窃外周边的径向位移: ,=-[2-p,--4r+p】6-n b道周边围岩的变形 压力作亮票发生的麦周边国岩在 -00h-0 6-12) -房3h (6-15) 有: 由于是平面应变向题,故轴向应力为: (6-13) 0:=.(gg+g,) 6-16) B、内压分配法求围岩应力 B、内压分配法求围岩应力 斋提 巷道壁面围岩位移:-+.G-17 由(6一11)村外周边处径向位移: 性丹的持穷处变赞 ..d 工形有任其害时高的受纳情款 式(6-11)=式(6-17),于是 在=a处,即卷道壁面:g,p。,g。p A合E0+e0-20n-o4 (6-180 对积分,并令一a得巷道壁面围岩位移: (6-17)

(2)有裂晾国岩 设围岩有经向裂隙。其深度为d 沿岩石表面的径向压力可假定为: P.-4P (8-19助 的应力。 ,=-n. 6-10 gn-台-0 g=0 在裂隙岩体任一深度处(r(d): 例愿:P187 0,=0 a,=p (6-210 在梨隙岩体外边界处(红=d),压力为: Pa=TP 6-22) (2)有裂限围岩 §63卷道围岩应力分布的弹塑性力学分析法 围岩的被坏方式 在田岩内任一点(d<r(o0)的应力为 围岩的破坏方式是计算作用在支护结构上压力和支护设计的依据 「剪切破坏 o,=n号-子n,号-n 弹塑性 「坚硬岩体:脆性酸坏 拉伸破坏 软到岩体:塑性屈眼 -n-n 以下主要讨论剪切破坏 以圆形巷过为例,时论袖对称协况下的国岩驶坏方式 根据莫尔一伦准则。围岩破坏泰件: 剪切破坏 巷道周边围岩的破坏来件 破坏面与最大主平面夹角为 夏形坑道围岩酱切破坏方式 如图所示:在 =1的原岩应力状态下 周边各处玻坏机会均等,形成环形算切玻材

如图所示:在》1的原岩应力状下算切规 面发展超势,玻坏起始角为p。 当周边围岩发生剪切玻坏时,则有 由图(a) :dr-ga=rd0 a,=g.=1++21-es28】 即: =d0.ciga 于是得到: a装0叶。 极径 on 破坏起始角p r=aea-P)ctga -20 p=0 上式为算切破坏面选线方程 和p=元一日 线与巷道面垂直 切体破坏 线 二、围岩塑性区应力分析 r=a.e(0-p)etgo (6-24 1、力学棋型 设原岩应力为加g,支架反力为p: 巷道半径a,塑性区半径R。 ()塑性区:内径a,外径孔.,内压为 P,外压为0即 最大剪物体水 长皮 2)弹性区:内径R。,外径无穷大 =R- 内压为0即外压为0 T 研究方法:弹罗性理论 要性区应符合应力平衡方程和性 根典尔强皮准则=C+tg 条件 弹性区应演足应力平衡方程和弹性 片+ 气件: 既满足性条件 经收为: ,-0,-o,+eep2 (6-28)

3、塑做区国岩平衡来件 当·0anp 增中任一单元体在径向方向应平衡条件 .rd+20 drsi -(G.+do,Xr+dr)d0=0 政写为:-g 类标下的平衡青徽分方程: 中。 在巷道周边有:,, (6-26) C.l(p.tece)e 代入(a)式得: 代入(b)式得: (1-sino)do. in 于是得塑性区应力计算公式(修正的芬涅公式): tg-时 所以: 员器5高 ,=a+eeep兰+g-cgp (6-2) (e) T,o=0 将式(@)代入式(6-26)式: 可见:塑性区应力的大小只与围岩本身的力学特性 ,-0,=a,+egp品。 (6-26) (c,中)及其距轡道中心的距高r和辔道半径a有关,而与 原岩应力无关, (a) 适用条件,a≤r≤R 三、弹区的应力 0a-gm=2E-20 (b) 径为 内压力为 ,外压力为P的 当r=R时,即在弹塑性区交界面上,塑性区应力差由式(6-26): 况下,弹性区内半径为r处的应力 0-0,-(d,+c.c) (8-2) 1 .-p(l-Ri 即: d 下.=0 根据在弹塑性区边界应力相等的条件,则有式(b)=() 当=R时,印在弹塑性区交界面上,弹性区应力 2n-20=o+…egp品 Ga =2P,-0x 解得: -P (1-sing)-c.cos (6-28) 于是:0。-0w=2P-2ag (b) a+o=2P 将式(6-28)代入式(a)得弹性区的应力: (c)