
第三章弹性力学基本理论与方法 S3-1概迷 多31颜述 ■岩石力学(工程力学)问题求解特点: 事红基本方程 依据:边界约束条件 多玉3地界缘件与圣维南原圆 平衡徽分方程 534按位移求解平面问题 几何方程(形变与位移间几何关系) 535按应力求解平面问题 物理方程(应力与形变间物理关系) 求解:应力分量、形变分量和位移分量 目的:研究结构强度、稳定性、破坏、失效等 第三事弹修力本论与方 S3-1概述 §3-1概述 ■弹性力学基本假设1一连续性假设 ■弹性力学基本假设: 假定整个物体的体积都被组成这个物体的介质所 (1)连续性假设 填满,不留下任何空隙。 (2)完全弹性假设 理量,例如应 (3)均匀性假设 等等,才可能是连续 因而才可能 (4)各向同性假设 (5)小变形假设 第三事弹特力学善单理修与方法 第三事弹性力学基本理论与方记 S3-1概述 S3-1概述 弹性力学蓬本假设2一完全弹性假设 弹性力学基本假设?一均匀性假设 弹性,指的是“物体在引起形变的外力被除去以后 整个物体是由同一材料组成的。 能恢复原形”这一性质。 基于均匀性假设,整个物体的所有各部分才具有相 完全弹性,指的是物体能完全恢复原形而没有任何 同的弹性,因而物体的弹性才不随位置坐标而变,可以 利余形变。 取出该物体的任意一小部分来加以分析,然后把分析的 满足完全弹性假设,物体在任一爵时的形变就完全决定于它在 结果用于整个物体。如果物体是由两种或两种以上的材 料组成的,例如混凝土,那么,也只要每 -种材赵的 粒远远小于物体而且在物体内均匀分布,这个物体就司 不应力成形实的大小面 以当作是均匀的 性力学怎本与方
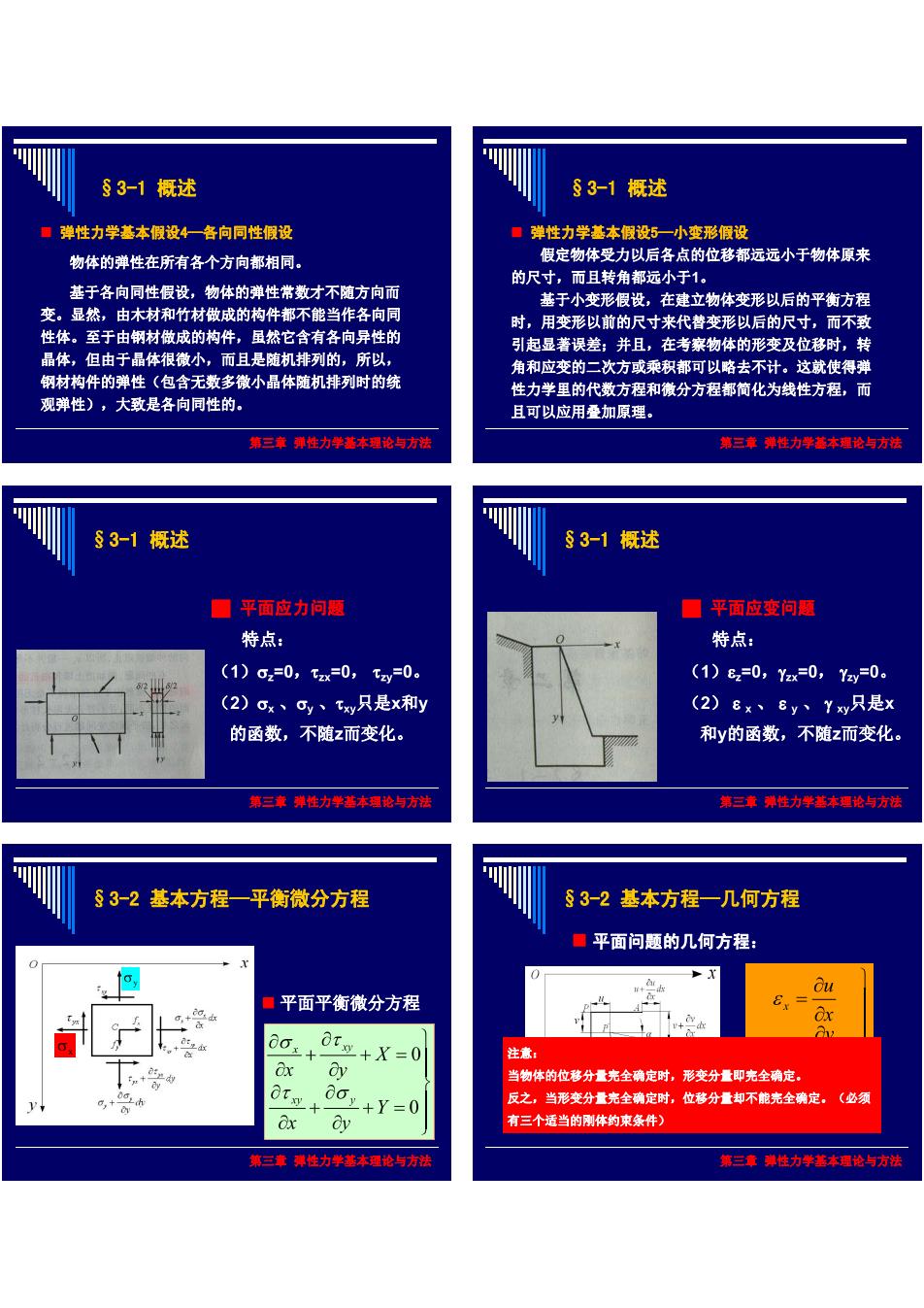
83-1概迷 S3-1概述 。弹性力学墓本假设4一各向同性假设 ·弹性力学基本假设5一小变形假设 物体的弹性在所有各个方向都相同 假定物体受力以后各点的位移都远远小于物体原来 基于各向同性假设,物体的弹性常数才不随方向而 的尺寸,而且转角都远小于1, 变。显然,由木材和竹材做成的构件都不能当作各向同 蒸于小变形假设,在建立物体变形以后的平衡方程 性体。至于由钢材做成的构件,显然它含有各向异性的 时,用变形以前的尺寸来代替变形以后的尺寸,而不致 晶体, 千品体很木 ,而且是随机排 引起显著误差:并且,在考察物体的形变及位移时,转 的弹性(包含无数多微小晶体随机排列时的统 角和应变的二次方或乘积都可以略去不计,。这就使得弹 大致是各向同性的 性力学里的代数方程和微分方程都简化为线性方程,而 且可以应用叠加原理。 剪三年明性力伊港本雪论与方能 第豆年弹性力学卷本理论与方港 3-1概述 §3-1概述 ■平面应力问糖 口平面应变问糖 特点: 特点: (1)o,=0,ta=0,ty=0。 (1)8=0,Ya=0,Y=0。 (2)ox、可,、ty只是x和y (2)ex、8y、Yy只是x 的函数,不随z而变化。 和y的函数,不随z而变化, 第三票弹性力华套本摩论与方陆 S3-2基本方程一平衡微分方程 §3-2基本方程一几何方程 ■平面问题的几何方程: .色 ■平面平衡徽分方程 +X=0 注意: 当物体的位移分量完全确定时,形变分量即完全确定。 +Y=0 反之,当形变分量充金确定时,位移分量如不能充金确定。(必须 有三个适当的刚体的束条件)
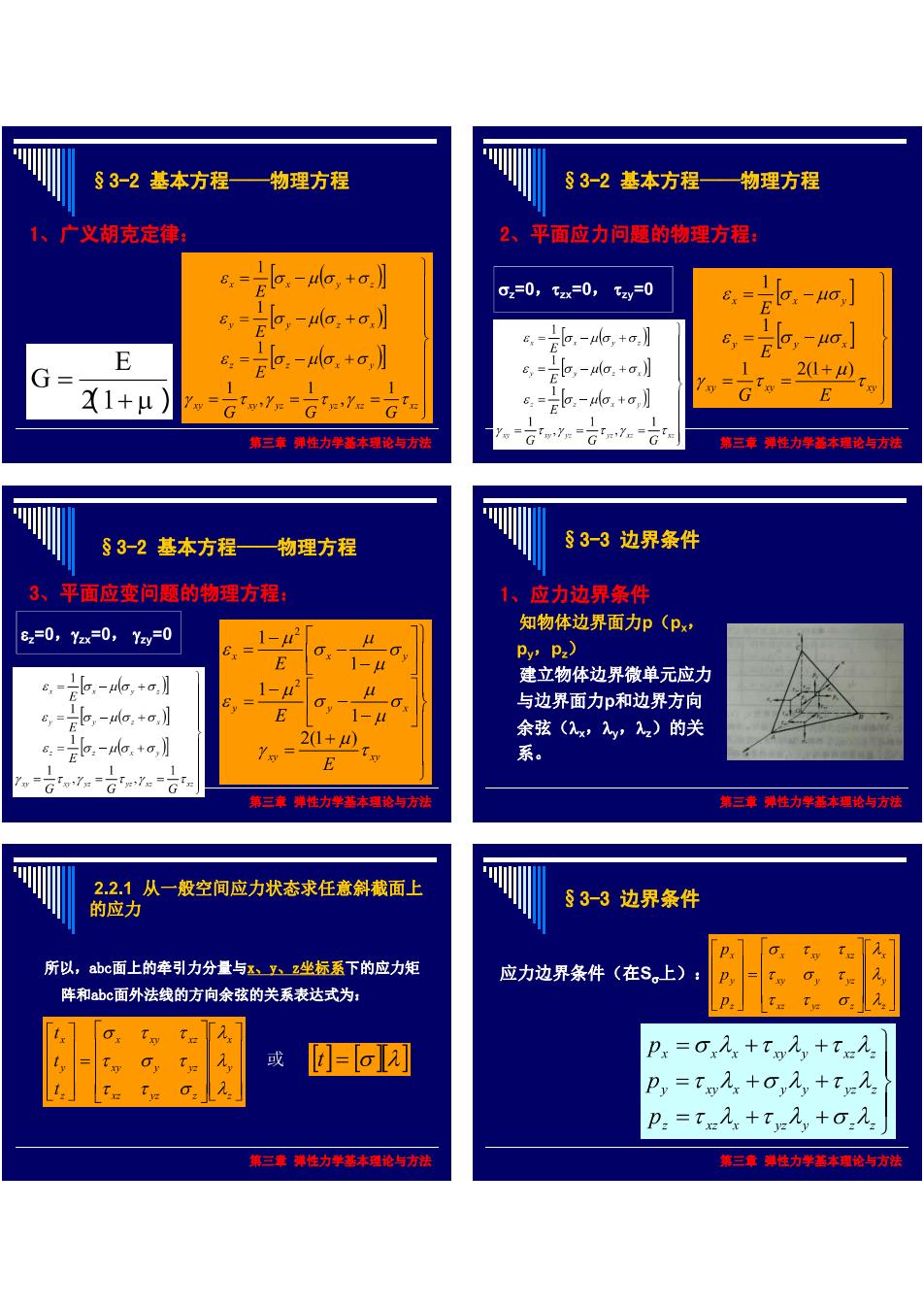
§3-2基本方程一物理方程 §3-2基本方程一物理方程 1、广义胡克定律: 2、平面应力问题的物理方程 6= a,-a,+a】 0,=0,tx=0,ty=0 8= 8,=b,-,+o,】 6,=,-MO. E G= ,-e+o 6■g,-g+ 20+0 X1+u) Gfu7n-GfmT-Gf &=Ea-o,+o,月 第三事弹力本论与方 第三弹力学卷本论与才 §3-2基本方程—物理方程 ©3-3边界条件 3、平面应变问题的物理方程 1、应力边界条件 B,=0,Yx=0,Yay=0 =1-2 知物体边界面力p(px, =,-,+o】 1-2 建立物体边界微单元应力 ,=b,-da,+o. 与边界面力p和边界方向 余弦(,,1)的关 系 上 n=Gfne-G 第三事弹格力小善本避论与方壮 第三事弹性力学基本建论与方记 2:2,1从一般空间应力状态求任意斜截面上 §3-3边界条件 的应力 所以,abc面上的牵引力分量与飞、坐标系下的应力矩 应力边界条件(在S。上) T O T 阵和abc面外法线的方向余弦的关系表达式为: 或 =o刀 t. p,=t+o,,+t入 P.=t+T-,+,2 第三性力学墨本理论与方

§3-3边界条件 §3-3边界条件 平面问题的应力边界条件(在S。上): 2、位移边界条件(在8上) 知物体边界上位移 p.=0入+tm入l 建立物体边界上点的位移与给定位移相等的条 D,=tn,+0,人 u=u,v=v,W=w 第三套弹隆力学基本路论与方法 第三年弹性力学卷本理论与方港 3-3边界条件 §3-2基本方程一平衡微分方程 3、混合边界条件 图3-2 知物体边界上部分应力、给定位移 建立物体边界上点的应力边界条件、位移边界 件。 + 第三车弹在力学春车睡轮与方性 第三票单性力学套本摩论与方性 §3-3边界条件 §3-4按位移求解平面问题 +-0 移以位移分为士 4、圣维南原理及其应用 未知西数 如果把物体的一小部分边界上的面力,变换为 =0 界条件中习 应力分量和死 分布不同但静力等效的面力(主矢量相同,对于 同一点的主矩也相同),那么,近处的应力分布 解出位移分量,搭无 求出形变分量和应力分量 将有显著的改变,但是远处所受的影响可以不计 平面力物理方: (u以=UsHV以=Ms) -ug 边界条日g+mx》=F(s (mc+t=f,(s
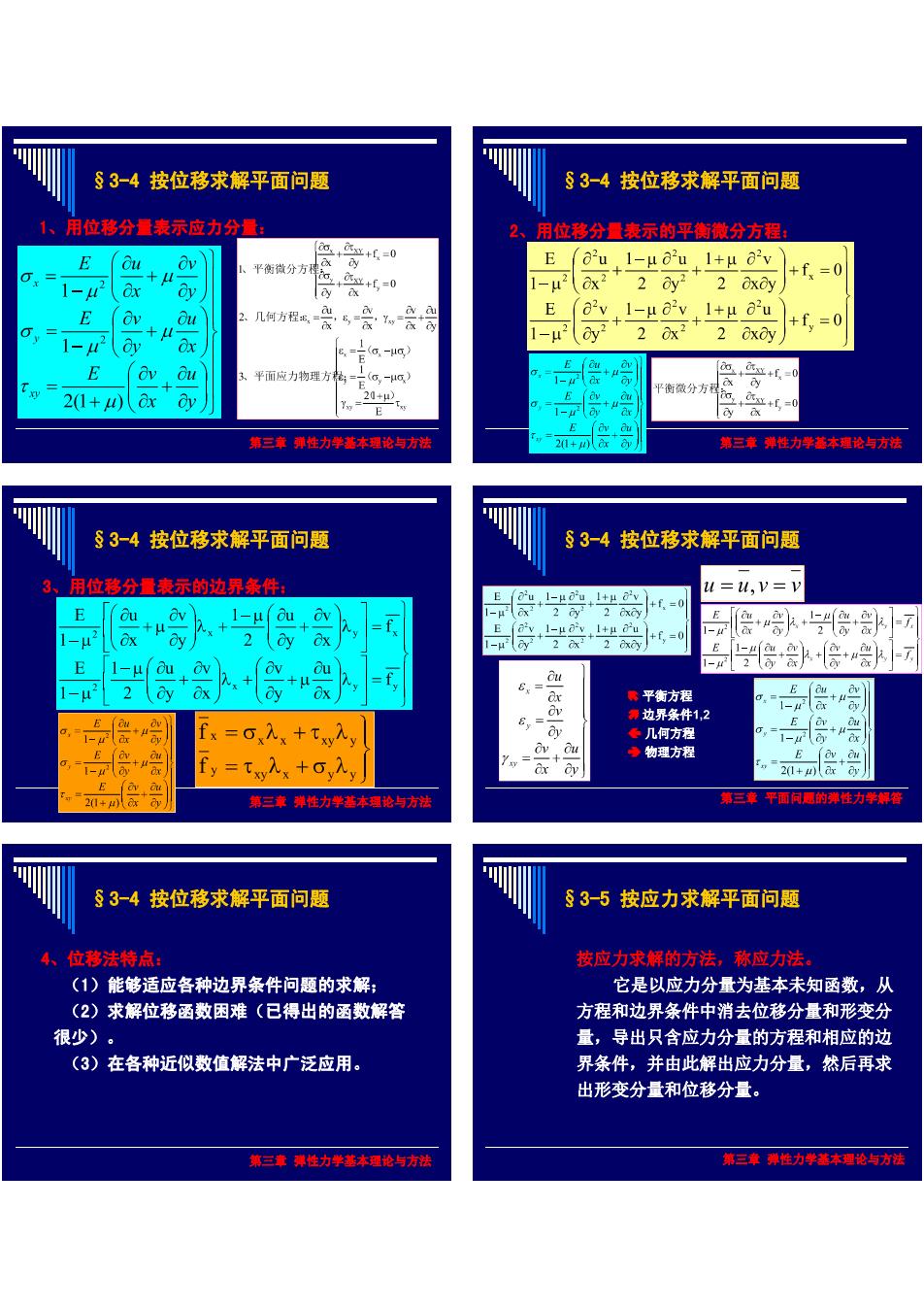
§3-4按位移求解平面问题 §3-4按位移求解平面问题 1、用位移分量表示应力分量 2 用位移分量表示的平衡微分方程: E 平衡微分方 +=0 E_u+1-μau+1+uav +f=0 +5=0 E tf。= 1-2y + 1-u20v2 20x2 6.-E(.-HG 平正应力物理方构-6 衡资分方 21+4)xy 第三重弹作力学卷本理论与为法 §3-4按位移求解平面问题 §3-4按位移求解平面问题 用位移分童表示的边界条件: 1=14,=V E a =f I-H ou av fx=入+T入 fy=t入+,入 第三事弹格力学善单理修与方法 第三塞平雷问意的佛性为学解招 §3-4按位移求解平面问题 §35按应力求解平面问题 4、位移法特点 按应力求解的方法,称应力法 (1)能够适应各种边界条件问题的求解: 它是以应力分量为基本未知函数,从 (2)求解位移函数困难(已得出的函数解答 方程和边界条件中消去位移分量和形变分 很少) 量,导出只含应力分量的方程和相应的边 (3)在各种近似数值解法中广泛应用。 界条件,并由此解出应力分量,然后再求 出形变分量和位移分量。 第三卷力学本论与方

§3-5按应力求解平面问题 §3-5按应力求解平面问题 应变分量表示的几何方程(形变协调方程、相容 1,应变分量表示的几何方程(形变协调方程、相容 方程) 方程) aE.,62e02y 求e,对y的 二阶导数: 求e对x的 a26 8-r 连续体的形变分量6、8y、Y不是互相独立的 a 而是相关的,它们之间必须满足相容方程, w=+ 二阶导数; ar? 才能保证对应的位移分量u和v的存在。 三性力学本与方 §3-5按应力求解平面问题 §35按应力求解平面问题 平面应力情况: 2、用应力分量表示的相容方程 Ot.. 平面应力情况: +f,=0 +o,)上+g+ 平面应变情况 x dy 是小 平面应变情况: + =O+t入 下平衡方程 2 10 个相容方程 1-u cx dy 香边界条件。 第三事弹传力学卷本避论与方社 第三事性力学本绳论与方港 §3-5按应力求解平面问题 §3-5按应力求解平面问题 ■单连体:只有一个连续边界的物体 3常体力情况下的简化 应力西数 平面应力情况: 在常体力情况,即体力分 ■多连体:具有两个或两个以上的连续边 界的物体。(还必须满足位移单值条件) 平面应变情况: 小 +%+a,)人0 82 02 三性力本建论与方法 第三年力港本理论与方

§3-5按应力求解平面问题 §3-7按应力求解平面问题 3、常体力情况下的简化应力函数 3、常体力情况下的简化应力函数 0六y +f=0 o+o =0 V2(o+o =0 +f,-0 y ◆平衡方程: 相容方程: ,=g+,, 事边界条件。 §3-7按应力求解平面问题 §3-7按应力求解平面问题 当体力为常量时在单连体的应力边界间题中, 3、常体力情况下的简化应力函数: 如果两个弹性体具有相同的边界形状,并受到同 样分布的外力,那么,就不管这两个弹性体的材料 a.Ot+f=0 是否相同,也它们是在平面应力情况或是在平面 应变情况下,应力分量的分布是相同的: +E=0 da, =0 但是,两种平面问题中的应力分量,以及形变和 平衡 程是一 个非齐 位移却不一定相同。 对应齐大微分方程的适解。 =0 第三意身峰力座誉求理论与方法 第三布帅性力学连本理论与方法 §3-7按应力求解平面问题 §3-5按应力求解平面问题 3、常体力情况下的简化应力函数 3,常体力情况下的简化应力西数 0o. 2+f=0 特解:o=fx,c,=fy,飞y=01 =0 求解齐次方程通解需要用到“偏母数 具有相容性”徽分方程理论: 或:,=0,y=0,tw=fy-千yx +f=0 或:ox-fx-yy=fx-fy 0 ox ay' Oy Ox Txy=0; 等等 第三力学蓬本塑论与方

§3-5按应力求解平面问题 §3-5按应力求解平面问题 常体力情况下的简化应力函数 3,常体力情况下的简化应力函数 0Φ 0Φ a2 代入相容方程, a 得到: y =0 +o,小0 + =0 =8'D 82Φ +2+心-0应力函数相容方程 v中=0减中=0 量三性力学本壁论与方 §3-5按应力求解平面问题 §3-5按应力求解平面问题 4、迎解法与半逆解法多项式解答 conclusion,按应力求解平面问题,可以 ▲逆解法:先设定各种形式的、满足相容方程的 归纳为求解一个应力函数Φ,它必须满足 应力函数,再由此求得应力分量,然后根据边界 相容方程,边界条件:在多连体中,还必 条件,看这些应力分量对应于边界上什么样的面 须满足位移单值条件。从上述条件求解出 力,从而得知所选取应力函数可以解决的问题。 讨论: 应力函数Φ后,便可依次求出应力分量, =a+bx+cy; 应变分量和位移分量。 p=ax'+bxy+cy Φ=ay, 第三事弹传力学卷本避论与方法 第三套佛性力学塞本绳论与方港 §3-5按应力求解平面问题 §3-5按应力求解平面问题 艾里应力函数心 4、逆解法与半逆解法多项式解答 +-0 ▲半逆解法:先针对所要求解的问题,根据弹性 2” 体的边界形状和受力情况,假设部分或全部应力 分量的函数形式:并推出应力函数形式:然后代 入相容方程,求出应力函数的具体表达式;再求 出应力分量,并考察其是否满足全部边界条件。 6-E(c.-uc 平面应力物理方: -ug [(u)=U(sH(v)=v(s) 直到所有条件全部满足。 边界条aa+m=f(s (mc+l-t=T(s 三性力本理论与方

§3-5按应力求解平面问题 §35按应力求解平面问题 5、矩形果的纯弯曲 5、矩形象的纯弯曲 设有矩形截面的长梁(长度L远大于深度h),它 解:采用逆解法 的宽度远小于深度和长度(近似平面应力问题) (1)设定应力函数:①=ay: 或者远大于深度和长度(近似平面应变问题), (2)求应力分量: 1+mw=」 在两端受相反的力偶而弯曲,体力可以不计。 x=6ay:Cy=0:txy=tyx=0 (mG +lts=(s (3)考察边界条件,定系数 上下边界:(ay)yw=0: txy)yth2=0 §3-5按应力求解平面 §35按应力求解平面问题 矩形的纯弯曲 5 矩形果的纯弯曲 解:(3)考察边界条件,定系数: (u)s =)s=Ms) 解:(4)求取应力: 左右端边界: 00 0,+m-ts=f (S (tx)=0: mg+r,=可s》 ,=6ay=12My/h=My/I;,-0;t,=tyx=0 ()0=0 a =2M 讨论! 0,=6ay:0y=0:下gy=5y.=0第三事净隆力净善本理论与方祛 第三角中推力参置求壁论与力法 §3-5按应力求解平面问题 §35按应力求解平面问题 5、矩形梁的纯弯曲 5、矩形果的纯弯曲 解:(5)求取形变分量: (6)求取位移分量: 将上述应力分量代入物理方程,解之得形变 将上述形变分量代入几何方程,得: 分量: M =0 M …最后根据边界条件得: =(g,-μ = uM 20+. 第三事力本理论与方性

§3-5按应力求解平面问题 §3-5按应力求解平面问题 6、箭支重受均布着管 6、简支象受均布椅载 设有矩形截面的简支梁,宽度为1个单位,深度为 解:应用半逆解法求解。 h,长度为2L,体力可以不计,受均布荷载q,由 (1)假设应力分量的函数形式:σ,=寸(y) 两端的反力ql维持平衡。 (2)推求应力函数形式: a 于0+o+0 §3-5按应力求解平面问题 N §3-7按应力求解平面问题 6、 简支聚受均布荷敏 6、 简支景受均布荷较 解:(3)由相容方程求解应力函数: 解:(4)由应力函数求应力分量: =三4++0+D+++0 (64y+2B)+x6Ey+2F)-2A4y2-2By2+6y+2K 7,=A3+2+G+D Tr= x(342+2By+C-(3Ey2+2F+G 第三事弹性力学卷本避论与方法 第三事平面间哪的弹桂为学解管 §3-5按应力求解平面问题 §3-5按应力求解平面问题 ,-6d+2+66+2F-2-22+6 6y2B-2Ay-28y6y2冰 筒支梁受均布荷前 -32+2y+C-3y2+2y+ 6 简支受均布荷 解:(5)考察边界条件: 解:(5)考寨边界条件: a、对称性E=F-G-0 a、对称性E=F-G-0 A= b、上下边界(主要边界) b、上下边界(主要边界) c、左右边界(次要边界) c、左右边界(次要边界) B=0 0