
部分矿山岩体变形、破坏形式 第二章 应力与应变 底题 变形 沉陷 ■落 2.2体力和面力 2.2体力和面力 ■体力: 内任 分布在物体整个体积内部各个质点上的力, 在P点的的 又称为质量力。 均集度为 例如物体的重力,惯性力,电磁力等等。 AF 2.2体力和面力 2.2体力和面力 。一毅来讲,物体内部各点处的体力是不相同的。 ■面力: 分布在物体表面上的力称面力。 例如风力,静水压力,物体之间的接触力等。 致为正,反之为负。 ●在弹性力学中,体力是指单位体积的力。它们的因次是 [长度

2.2体力和面力 2.2体力和面力 、对于物体表面上的年 ■内力:物体在外界因素作用下,物体内部各个部分之 点的面力 间将产生相互作用,物体内部相互作用力称为内力。 。面力矢量是单位面积上的作用力,面力是磷 内力的计算可以采用裁面法,即利用假想平面将物体 截为两部分,将希望计算内力的截面暴露出来,通过平衡 ·雪资歌标用12 =F 关系计算裁面内力F。 ■应力:指单位面积的内力, [力[长度] 22 体力和面力 2.2体力和面力 。内力的分花 般是不均匀的。为了措述任 正应。 应力在其作用戴面的法线方 在 向的分量,称正应力。 面积上 力主 市是均匀的。设 ■切应力:应力在其作用裁面的切线方 向的分量,称切应力。 AF =A5 因此说 ·幽水 是通过任意点M,法线方向为的徽分面 确定了 [力Ⅱ长度 2.2体力和面力 2.2体力与面力 为资产数梵资赞高高的状来微利用是锦美密帮 ■正面:外法线沿着坐标轴的正方向的藏面。 正面上应力正负规定:沿坐标轴正向为正,沿坐标 单完 轴负向为负。 角而。 外法线是沿着坐标轴的负方 的截面 负 应力正负规定:沿坐标轴正向为负,沿坐标 轴负向为正
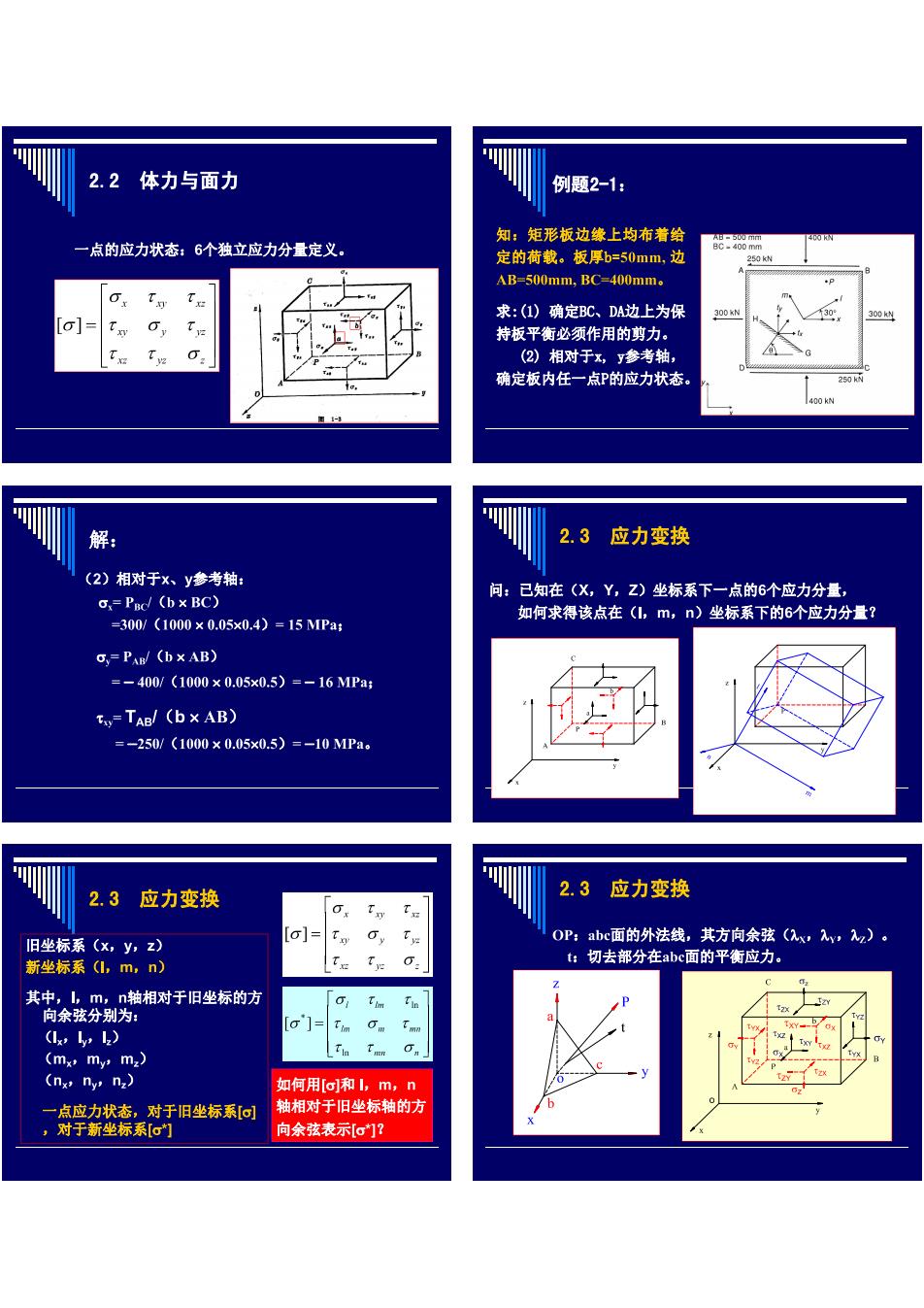
2.2体力与面力 例题2-1: 知:矩形板边缘上均布着给 一点的应力状态:6个教立应力分量定义 定的荷载。板厚b=50mm,边 AB-500mm,BC-400mm. .P a]=Ta 求:(1)确定BC、DA边上为保 持板平衡必须作用的剪力。 (2)相对于x,y参考轴 确定板内任一点P的应力状态 解 2.3应力变换 (2)相对于x、y参考轴: x=Pid/(bx BC) 问:已知在(X,Y,Z)坐标系下一点的6个应力分量, =300/(1000×0.05x0.4)=15MPa: 如何求得该点在(l,m,n)坐标系下的6个应力分量? =PAW/(bxAB) =-400/(1000×0.05x0.5)=-16MPa: Ty-TAB/(bxAB) =-250/(1000×0.05x0.5)=-10MPa 23应力变换 2.3应力变换 I旧坐标系(x,y,z) OP:abc面的外法线,其方向余弦(,X,X)。 新坐标系(,m,n) t:切去部分在abc面的平衡应力。 英中余铁分别相对于旧坠标的力 =T o D a, 何用o和1 向余弦表示[ā]?

2.3.1从一般空间应力状态求任意斜截面上 231从一般空间应力状态求任意斜载面上 的应力 的应力 假设abc面的外法线P由用方向余弦( P 利用方向的静力平衡条件得出: 、入、入)的行矢量定义。 th-c,从-t从-从0 即:to,入++ 同理可推出:对于、方向对应的关 ac =,0ab面-A=从,0bc面 于,的表达式: =A=A入 t+G,+ 假定牵引力矢量t的分量为t ti=takt tniy Grh 修二事虚力与商里 修二手围为药康里 所以,bc面上的牵引力分量与x、黑、坐标系下的应力矩 同理,bc面上的牵引力分量与L、m、n坐标系下的应力矩 阵和abc面外法线的方向余弦的关系表达式为: 阵和abc面外法线的方向余弦的关系表达式为, 北 或 =oI] a团 第事童力与意复 2.3.2坐标变换对应的应力变换方程 2.3.2坐标变换对应的应力变换方程 根据矢量分析,矢量[们按照如下变换方程从一组正交参 利用上述旋转矩阵的性质,再看[]和[、[】和[】之 考坐标、予、z变换到另一组参考坐标1、、 间的关系式 [t=[R[t]或[t]=Rr[ m.mt.nt. ]-(RIv] [=RIJJ-Rr 则:[t]=[RJ[t]=[RJ[o][J=[RJ[o[RJr[】 上式中, [R为旋转矩阵, 该矩阵的行可看作是由新轴相对 由于:【=[】 日轴的方向余弦的 行矢重组成的。该旋转矩阵的唯一性性质 于是:[o门=[R][o]RJ(应力变换方程) 是其逆阵等于它的转置,即:风=风了

232坐标变换对应的应力变换方程 2.3.2坐标变换对应的应力变换方程 应力变换方程扩展式: 坐标变换情况下应力分量的显式表达。 1.1.Tax m m.my m.Ts C,T 坐标变换情况下应力分量的显式表达: -l,2a,+2a+l2o,+2(,,tll,+1lx) tim=I,m,c,+lm,c+l,m,c,+I,m,+l,m,t+ +(Ln+ln,(Ln,+ln,)tw +(m,+m,)飞+(m,+lm,)。 事为康 2.4应力不变量 2.4应力不变量 : 设图2-4(2)割面正是一个主平面 主应力:作用在主平面上的正应力。 牵引力 外法线(2,,) 牵引力分量: 按丽代数值的大小排列为:c2©,2@ 玉野报瑰实岛的费餐 工事意力与意变 第事原力与康 2.4应力不变量 ,4应力不变量 ,-0。 7 -。 =C 三个联立齐次线性方程组:根据高等数学中有关线性组 的理论,该方程组有非零解的必要与充分条件是这个方 o-1o6+1,0p-4=0 程组的系数行列式A-0

2.4应力不变量 2.4应力不变量 主应力的方向余弦: 它们由下 a,-01 Tw G.- 1=0+0,+0 r I 0.-0. 12=0,+0,+0,0,-(r号+t2+) =00,:+2r-(ot+0,+0) =A(4+B2+C月2,=B4+B2+Cp,入,=C(+B2+C 第二事金为与商 第三年画步海应里 2.4应力不变量 2.4应力不变量 主应力轴之间正交: 球形(静水)分量与偏斜分量: 检验正交性的条件是方向余弦矢量的三个点积的每一个 Te 必须为零,即: ]= 800 几2+元,2+元122=0 C. 偏斜主应力: 2223+元2y3+元223=0 52-0-)=01- =22-,-0)=0- 223+元1入3+九1几3=0 52,-a-a)=0-g 2.4应力不变量 2.5平面问题和双轴应力 应力偏量不变量: t 0 2=0G-a,2+o,-2+G,-a -(Fw+++Fg)

例题2-1:知矩形板边缘 G,=15MPa 上均布着给定: 的荷 截。板厚 50mm长50nmm长0m t.,=-10MPa 长。 (3)轴的方向余弦 1=c0s30°=0.866 l,=cos60°=0.5 m轴的方向余弦: 对于所示的 定应力分 所以 时的方向 其外法 66x15+0.5x -11.24934-4-8.66 -1.41(MPa) 解 解 (3 g=m,'o,+m,2g,+m,2g,+2(m,m (4)最大主应力 (-0.5)2x15+0.866x(-16) 0.5)×0.866×(-10 ) (a.to).-ar =3.75-11.9993+8.66=0.41(MPa) m-l,m,@+lm,g,+lm,g+(1,m,+l,m,)飞,+ +Lm+L,m,)ty+Lm,+1m,)to 0500-5)x15+0-5x06X416r0.366x036+n5 最大主应力方向(相对×轴),=20,1 9284.99956=-18.42 ■产童度动与度 ■三童夏力与度业 解 解: (5)当0=90°时:12=0,入=1,入2=0 (5)当9=0°时:11,入=0,入=0 0+ to+入y-10(Pa) t入+-15(a) t,tw入+o,λ=-16(Pa) t入+C,入+-10(Pa 当060°时:=0.5,=0.866,0 t6,+15x0.5-10x086=-1.6(a 89 (MPa

作业1: 作业1:( 如图中所示的盖位离体,在正六 见面上 作用有平行于给定 (2)试 方间余的 的的应为分 困形完整 确定x,y,z坐标系中的 上面(1)中建立的应力分量 25 轴相对于x,y,z的 的特 正方程 各主应力值利 (0,1,)=0.281,0.597,0.750 轴的方向角 证正明主】 相互正交的 (m,m,m,)-(0.844,0.219.-0.490) m,n.,m)=(-0.457.0.771,-0.442 2.6位移和应变 2.6位移和应变 u=u,+d加,式中d加, ax dx ou dy dz g =u,+d加,式中d,= ,=u,+du,式中du,= 第三年度为与位口 第二事童为与康 26位移和应变 2.6位移和应变 位移增量的矩阵表示: (1)刚体旋转 绕轴发生刚体转动口,对 相对传孩的组成: 应的Q相对于P的相对位移 刚体旋转+单元变形 分量为: 0 du --Q dz; du-,dy. [d]=[D][dr]
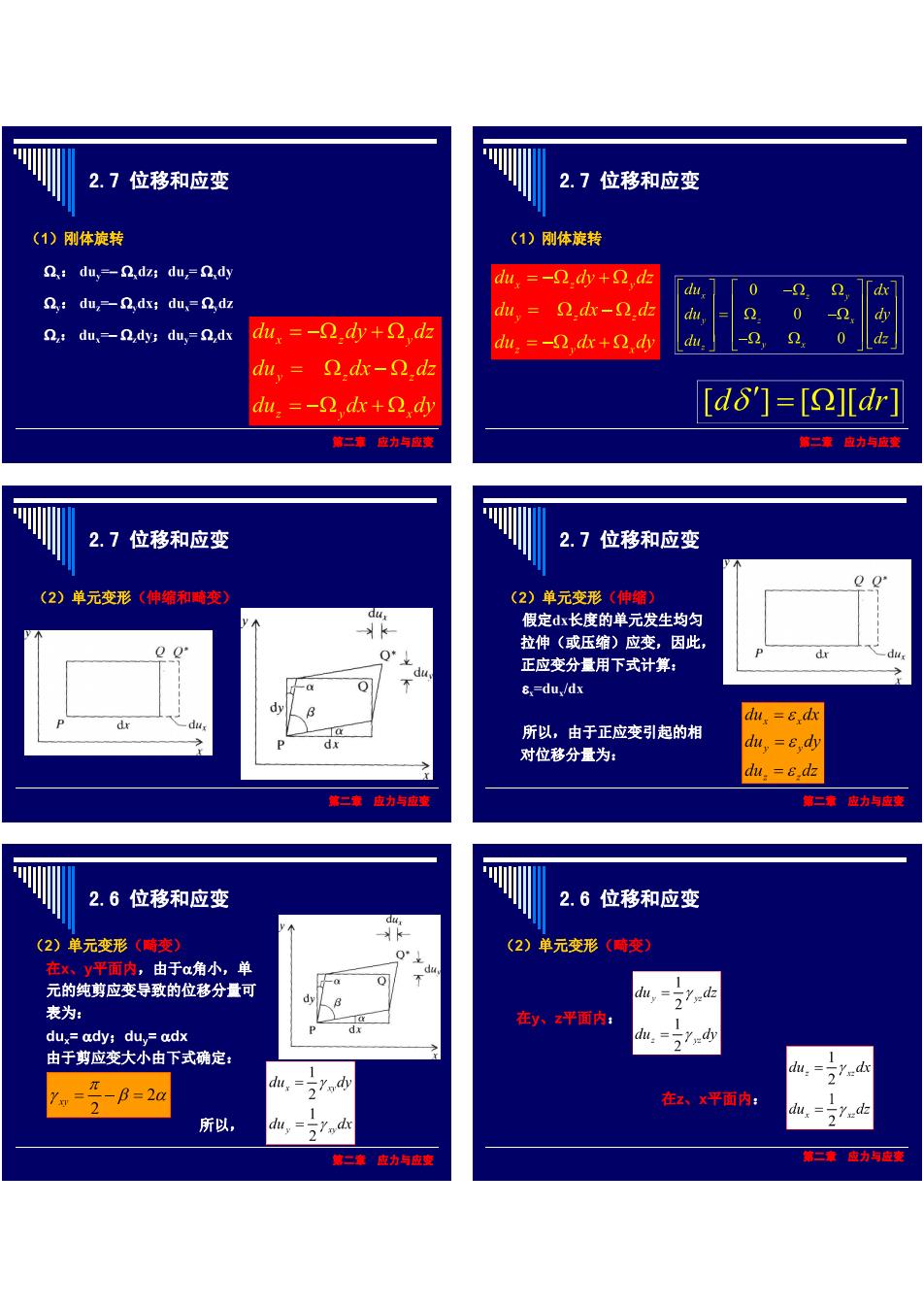
2.7位移和应变 2.7位移和应变 (1)刚体旋转 (1)刚体旋转 du,-dz:du=dy du=-2.y+2.d西 du,-dx:du,=dz 0-,1「 du,=.dx-n.dz 0.0- du,=dy;du,=Qdx du.=-2.d+2.d d=-2,d+2山 0 du,.dx-.dz du,=-2 dx+dy 「d8]=[Ωldr 2.7位移和应变 2.7位移和应变 (2)单元变形《钟和变 (2)单元变形 假定山长度的单元发生均匀 拉伸(或压缩)应变,因此 正应变分量用下式计算: a 8.=du,/dx d 所以,由于正应变引起的相 对位移分量为: d,=e,4 管过重成九与度 ■童度动与度童 2.6位移和应变 2.6位移和应变 (2)单元变形(畸变) (2)单元变形《崎变) 在、平重内,由于a角小,单 元的纯剪应变导致的位移分量可 a d,=.4 表为: 在y、平面内 du.= 由于剪应变大小由下式确定: 2 n=7-B=2a 在红x平面内: l,= 所以 事二市富力海康更

2.6位移和应变 2.6位移和应变 (2)单元变形(伸+骑 (2) 元变形《钟塘+复 u,E dy , 4.=6.db 血,=.+小+7 血,7+,+ [dδ"T=[e][dr] =yk+与+6 2.6位移和应变 2.6位移和应变 (3)相对位移(刚体鞋转+件婚+腾变) (3)相对位移(衡体童转+件增+确变) [d6]=[d6]+[d8T 正应变分量: 0 0 数整 1 事二事信方车套动 2.7主应变、应变变换、体积应变和 偏斜应变 2.8岩土力学中关于位移、应变和应 力的规足 应变变换方程 e]=[R][e][R] (1)沿坐标轴正方向作用的力和位移分量为正。 (2)收缩正应变取为正 体积应变: &x++8 (3)压缩正应力取为正。 c,-4/3 (4)若截面内法线相对于坐标原点向内指,则戴面上剪 偏斜应变 6-△/3y 应力方向相对于坐标原点向内为正,反之亦然。 6-A/3 事三章直力业