
第2章线性表 2.1线性表的定义 2.2线性表的顺序表示和实现 2.3线性表的链式表示和实现 2.4双向链表 2.5一元多项式的表示及相加
第2章 线性表 2.1 线性表的定义 2.2 线性表的顺序表示和实现 2.3 线性表的链式表示和实现 2.4 双向链表 2.5 一元多项式的表示及相加

线性结构(线性表、栈、队列、串) 线性结构是最常用、最简单的一种数据结构。 而线性表是一种典型的线性结构。其基本特点是线 性表中的数据元素是有序且是有限的。在这种结构 中: ①存在一个唯一的被称为“第一个”的数据元素; ②存在一个唯一的被称为“最后一个”的数据元素; ③除第一个元素外,每个元素均有唯一一个直接前驱; ④除最后一个元素外,每个元素均有唯一一个直接后继
线性结构(线性表、栈、队列、串) 线性结构是最常用、最简单的一种数据结构。 而线性表是一种典型的线性结构。其基本特点是线 性表中的数据元素是有序且是有限的。在这种结构 中: ① 存在一个唯一的被称为“第一个”的数据元素; ② 存在一个唯一的被称为“最后一个”的数据元素; ③ 除第一个元素外,每个元素均有唯一一个直接前驱; ④ 除最后一个元素外,每个元素均有唯一一个直接后继

2.1线性表的定义 线性表(Linear List):是由n(n≥0)个数据元素(结点)a1, a2an组成的有限序列。该序列中的所有结点具有相同 的数据类型。其中数据元素的个数称为线性表的长度。 当n=0时,称为空表。 当n>0时,将非空的线性表记作:(a1,a2,.a) a1称为线性表的第一个(首)结点,a称为线性表的最后一个 (尾)结点。 a1,a2…a都是a(2≤i≤n)的前驱,其中a1是a的直接前驱; ai+1, a#2…an都是a(1≤≤n-l)的后继,其中a+1是a的直接 后继
2.1 线性表的定义 线性表(Linear List) :是由n(n≧0)个数据元素(结点)a1, a2…an组成的有限序列。该序列中的所有结点具有相同 的数据类型。其中数据元素的个数n称为线性表的长度。 当n=0时,称为空表。 当n>0时,将非空的线性表记作:(a1,a2,…an ) a1称为线性表的第一个(首)结点,an称为线性表的最后一个 (尾)结点。 a1,a2…ai-1都是ai (2≦i≦n)的前驱,其中ai-1是ai的直接前驱; ai+1,ai+2…an都是ai (1≦i≦n-1)的后继,其中ai+1是ai的直接 后继

线性表的逻辑结构 ◆线性表中的数据元素a:所代表的具体含义随具体应用的不 同而不同,在线性表的定义中,只不过是一个抽象的表示符 号。 ◆线性表中的结点可以是单值元素(每个元素只有一个数据 项)。 例1:26个英文字母组成的字母表:(A,B,、Z) 例2:某校从1978年到1983年各种型号的计算机拥有量的变 化情况:(6,17,28,50,92,188) 例3:一副扑克的点数(2,3,4.,J,Q,K,A)
线性表的逻辑结构 ◆线性表中的数据元素ai所代表的具体含义随具体应用的不 同而不同,在线性表的定义中,只不过是一个抽象的表示符 号。 ◆线性表中的结点可以是单值元素(每个元素只有一个数据 项) 。 例1: 26个英文字母组成的字母表: (A,B,…、Z) 例2 :某校从1978年到1983年各种型号的计算机拥有量的变 化情况:(6,17,28,50,92,188) 例3 :一副扑克的点数(2,3,4…,J,Q,K,A)
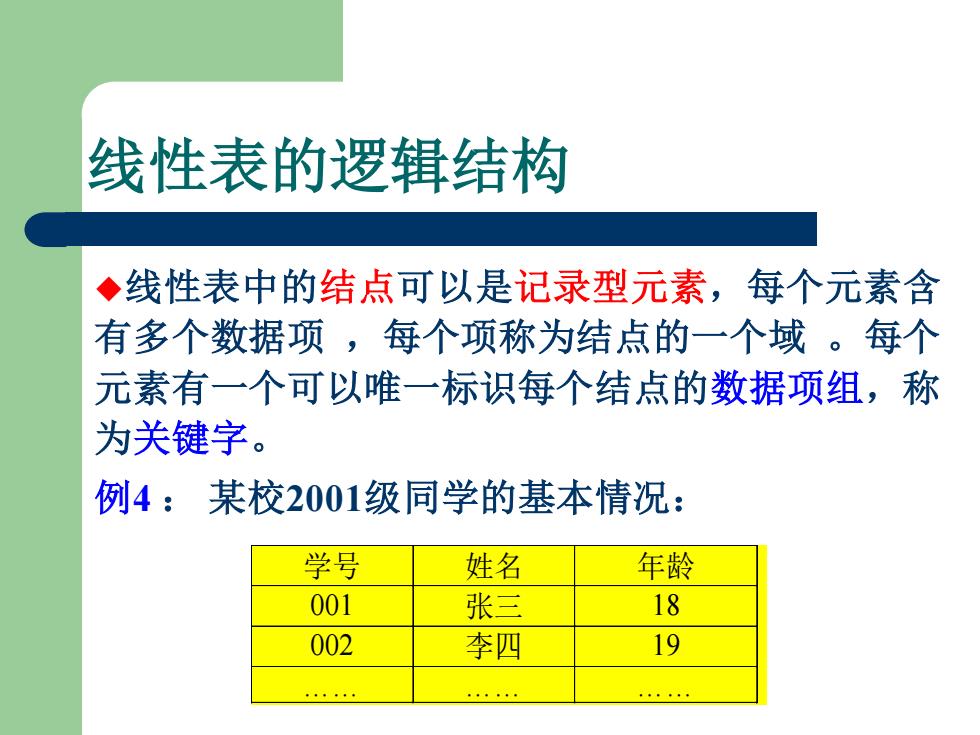
线性表的逻辑结构 ◆线性表中的结点可以是记录型元素,每个元素含 有多个数据项,每个项称为结点的一个域。每个 元素有一个可以唯一标识每个结点的数据项组,称 为关键字。 例4:某校2001级同学的基本情况: 学号 姓名 年龄 001 张三 18 002 李四 19 ···……
线性表的逻辑结构 ◆线性表中的结点可以是记录型元素,每个元素含 有多个数据项 ,每个项称为结点的一个域 。每个 元素有一个可以唯一标识每个结点的数据项组,称 为关键字。 例4 : 某校2001级同学的基本情况: 学号 姓名 年龄 001 张三 18 002 李四 19 …… …… ……

线性表的逻辑结构 ◆若线性表中的结点是按值或按关键字值)由小到 大或由大到小)排列的,称线性表是有序的。 ◆线性表是一种相当灵活的数据结构,其长度可根 据需要增长或缩短。 ◆对线性表的数据元素不仅可以访问,还可以进行 插入和删除等操作
线性表的逻辑结构 ◆若线性表中的结点是按值(或按关键字值)由小到 大(或由大到小)排列的,称线性表是有序的。 ◆线性表是一种相当灵活的数据结构,其长度可根 据需要增长或缩短。 ◆ 对线性表的数据元素不仅可以访问,还可以进行 插入和删除等操作

线性表的抽象数据类型定义(1) ADT List 数据对象:D={a|a:∈ElemSet,=1,2,,n,n≥0} 数据关系:R={a1,a>|a1,a:∈D,i=2,3,,n} 基本操作: InitList(&L) 操作结果:构造一个空的线性表L; ListLength(L) 初始条件:线性表L已存在; 操作结果:返回L中数据元素个数;
线性表的抽象数据类型定义(1) ADT List{ 数据对象:D = { ai | ai∈ElemSet, i=1,2,…,n, n≧0 } 数据关系:R = { | ai-1 , ai∈D, i=2,3,…,n } 基本操作: InitList( &L ) 操作结果:构造一个空的线性表L; ListLength( L ) 初始条件:线性表L已存在; 操作结果:返回L中数据元素个数;

线性表的抽象数据类型定义(2) GetElem(L,i,&e) 初始条件:线性表L已存在,I≤i≤ListLength(L); 操作结果:用e返回L中第个数据元素的值; ListInsert (L,i,&e) 初始条件:线性表L已存在,1≤i≤ListLength(); 操作结果:在线性表L中的第个位置插入元素e; }ADT List
线性表的抽象数据类型定义(2) … GetElem( L, i, &e ) 初始条件:线性表L已存在,1≦i≦ListLength(L); 操作结果:用e返回L中第i个数据元素的值; ListInsert ( L, i, &e ) 初始条件:线性表L已存在,1≦i≦ListLength(L) ; 操作结果:在线性表L中的第i个位置插入元素e; … } ADT List

线性表的基本操作(1) (1)初始化线性表InitList(&L):构造一个空的线性表L。 (2)销毁线性表DestroyList(&L):释放线性表L占用的内 存空间。 ●(3)清空线性表C1 earList(&L):将线性表重置为空表。 。(4)判线性表是否为空表ListEmpty(L):若L为空表,则返 回真,否则返回假。 ●(5)求线性表的长度ListLength(L):返回L中元素个数
线性表的基本操作(1) ⚫ (1)初始化线性表InitList(&L):构造一个空的线性表L。 ⚫ (2)销毁线性表DestroyList(&L):释放线性表L占用的内 存空间。 ⚫ (3)清空线性表ClearList(&L):将线性表重置为空表。 ⚫ (4)判线性表是否为空表ListEmpty(L):若L为空表,则返 回真,否则返回假。 ⚫ (5)求线性表的长度ListLength(L):返回L中元素个数

线性表的基本操作(2) (6)求线性表L中指定位置的某个数据元素GetElem(亿,i,&e): 用e返回L中第i(1≤i≤ListLength(L))个元素的值。 (7)定位查找LocateElem(L,e):返回L中第1个值域与e相等 的位序。若这样的元素不存在,则返回值为0。 (8)插入数据元素ListInsert(&L,i,e):在L的第i (1≤i≤ListLength(L)+1)个元素之前插入新的元素e,L的 长度增1。 (9)删除数据元素ListDelete(&L,i,&e):删除L的第i (I≤i≤ListLength(L))个元素,并用e返回其值,L的长度减 1
线性表的基本操作(2) ⚫ (6)求线性表L中指定位置的某个数据元素GetElem(L,i,&e): 用e返回L中第 i(1≤i≤ListLength(L))个元素的值。 ⚫ (7)定位查找LocateElem(L,e):返回L中第1个值域与e相等 的位序。若这样的元素不存在,则返回值为0。 ⚫ (8)插入数据元素ListInsert(&L,i,e):在L的第i (1≤i≤ListLength(L)+1) 个元素之前插入新的元素e,L的 长度增1。 ⚫ (9)删除数据元素ListDelete(&L,i,&e):删除L的第i (1≤i≤ListLength(L))个元素,并用e返回其值,L的长度减 1