
实习一晶体的目估投影与宏观对称观察 一.课前准备 1理解极射赤平投影原理。 2理解对称操作、对称要素、对称要素组合定理和对称型。 二、目的与要求 1.掌握极射赤平投影原理,用目估方法作晶体的极射赤平投影图 2。学会品体的对称操作,在晶体模型上找出其全部对称要素,确定品体所属的品 族和晶系。 3。能根据对称要素组合定理,在晶体模型上找出其全部对称要素,从而定出对称 型:并完成对称要素的极射赤平投影。 三.内容、方法和步骤 1.晶体的目估极射赤平投影 晶体的目估投影分两步走,第一步是进行球面投影,将晶面的位置标定在球面 上:第二步是将晶面在球面上的投影点,转换成平面投影点,进行极射赤平投影。 ()晶面目估极射赤平投影:在对晶面进行极射赤平投影时,首先将晶面进行球 面投彩,然后将投影球上半球的点与下目测点连线,与赤平面的交点即为它的极射 赤平投影点,在投影面上记“O”,下半球的点与上目测点连线,在投影面上记“×”。 上下半球上某两个点的极射赤平投影点重合,标记为“②”。 球面上位于赤道上的点,其极射赤平投影点将落在基圆上:两极上的点,其投 影点位于基圆的中心,其它点的投影都将落在基圆内。也就是说,晶体中水平晶面 的极射赤平投影点位于基圆中心:直立品面投影于基圆上:倾斜品面投影于基圆内 并且,近于直立的晶面的投影靠近基圆,近于水平的晶面的投影靠近圆心。 (②)直线的目估极射赤平投影:晶体中的对称轴和晶轴等均为直线,这些直线都 可以进行极射赤平投影。首先将直线平移,使之通过投影球球心,即可以确定直线 在球面上的两个交点,即其球面投影点,再将直线在球面上的两个交点分别与目测 点相连,与投影平面产生两个交点,将这两个交点用虚线相连就是该直线的极射赤 平投影。 水平直线的两个投影点在基圆上,其连线(虚线)为直径:直立直线的两个投 影点都位于基圆中心:倾斜直线的两个投影点都位于基圆内,其连线(虚线)为基
1 实习一 晶体的目估投影与宏观对称观察 一. 课前准备 ⒈理解极射赤平投影原理。 ⒉理解对称操作、对称要素、对称要素组合定理和对称型。 二、目的与要求 ⒈ 掌握极射赤平投影原理,用目估方法作晶体的极射赤平投影图 ⒉ 学会晶体的对称操作,在晶体模型上找出其全部对称要素,确定晶体所属的晶 族和晶系。 ⒊ 能根据对称要素组合定理,在晶体模型上找出其全部对称要素,从而定出对称 型;并完成对称要素的极射赤平投影。 三. 内容、方法和步骤 ⒈ 晶体的目估极射赤平投影 晶体的目估投影分两步走,第一步是进行球面投影,将晶面的位置标定在球面 上;第二步是将晶面在球面上的投影点,转换成平面投影点,进行极射赤平投影。 ⑴晶面目估极射赤平投影:在对晶面进行极射赤平投影时,首先将晶面进行球 面投影,然后将投影球上半球的点与下目测点连线,与赤平面的交点即为它的极射 赤平投影点,在投影面上记“O”,下半球的点与上目测点连线,在投影面上记“×”。 上下半球上某两个点的极射赤平投影点重合,标记为“ ”。 球面上位于赤道上的点,其极射赤平投影点将落在基圆上;两极上的点,其投 影点位于基圆的中心,其它点的投影都将落在基圆内。也就是说,晶体中水平晶面 的极射赤平投影点位于基圆中心;直立晶面投影于基圆上;倾斜晶面投影于基圆内, 并且,近于直立的晶面的投影靠近基圆,近于水平的晶面的投影靠近圆心。 ⑵直线的目估极射赤平投影:晶体中的对称轴和晶轴等均为直线,这些直线都 可以进行极射赤平投影。首先将直线平移,使之通过投影球球心,即可以确定直线 在球面上的两个交点,即其球面投影点,再将直线在球面上的两个交点分别与目测 点相连,与投影平面产生两个交点,将这两个交点用虚线相连就是该直线的极射赤 平投影。 水平直线的两个投影点在基圆上,其连线(虚线)为直径;直立直线的两个投 影点都位于基圆中心;倾斜直线的两个投影点都位于基圆内,其连线(虚线)为基

圆内的线段。 (3)平面的极射赤平投影:平面的延展后都和投影球相截成大圆。对球面上的大 圆讲行极射赤平投影时(基圆除外),只取上半球的半个圆讲行投影,使其上的每个 点都与南极相连,在投影平面上获得一系列交点,连成的一条曲线就是平面的极射 赤平投影。 与投影平面相平行的平面,其极射赤平投影的大圆与基圆重合:垂直于投影平 面的平面,其极射赤平投影的大圆表现为基圆的直径:与投影平面斜交的平面,其 极射赤平投影则为一大圆弧。 2.从晶体模型上找对称要素的一般方法 ()对称面(P)的确定:在品体中,可以没有对称面,也可有多个对称面,但最 多不超过9个。对称面在晶体中可能出现的位置为:①垂直并平分某些晶面和晶棱 的假想平面:②包含某些晶棱并通过角顶的假想平面。根据上述对称面的分布规律, 找出模型中所有的对称面。 (②)找对称轴(L)的确定:模型中对称轴的 分布规律为(图1-1):①垂直并平分品特的假粗直 线只能是之:②通过品面中心且垂直该品面的假 想直线可能是L2、L3、L4、L6:③通过角顶的假 想直线可能是L、L4、L6。根据上述对称轴的分 布规律,找出模型中所有的对称轴。注意:L无 实际意义,可以省略。 (③)找对称中心(C)的确定:在晶体中可没有 对称中心,若有则只能有1个,位于晶体几何中 图11立方体中对称轴的分布 心。对称中心的一般找法为:将模型每一个品面 分别贴于桌面上,如果都存在跟它反向平行的晶面,则该模型存在对称中心:如果 晶体上部出现棱或角顶,则该模型无对称中心。 3根据对称要素组合定理,推导出晶体棋型中全部对称要素 )低级晶族(三斜、单斜、斜方晶系):模型上无高次轴,当找到L时,将其 直立,再观察: ①有无与其垂直的L2,若有则必有2个L2同时垂直该L2,为3L2(L2×L24, →L22L2→3L2). ②有无包含L2的P,若有则必有2个P同时包含该L2(L2×P→L22P)。 ③有无与L2垂直的P,若有则该模型必有对称中心C(L2+Pu,一L2PC)。 (2)中级晶族四方晶系:模型上只有一个高次轴L,当找到L时,将其直立,再 观察:
2 圆内的线段。 ⑶平面的极射赤平投影:平面的延展后都和投影球相截成大圆。对球面上的大 圆进行极射赤平投影时(基圆除外),只取上半球的半个圆进行投影,使其上的每个 点都与南极相连,在投影平面上获得一系列交点,连成的一条曲线就是平面的极射 赤平投影。 与投影平面相平行的平面,其极射赤平投影的大圆与基圆重合;垂直于投影平 面的平面,其极射赤平投影的大圆表现为基圆的直径;与投影平面斜交的平面,其 极射赤平投影则为一大圆弧。 ⒉ 从晶体模型上找对称要素的一般方法 ⑴对称面(P)的确定:在晶体中,可以没有对称面,也可有多个对称面,但最 多不超过 9 个。对称面在晶体中可能出现的位置为:①垂直并平分某些晶面和晶棱 的假想平面;②包含某些晶棱并通过角顶的假想平面。根据上述对称面的分布规律, 找出模型中所有的对称面。 ⑵找对称轴(L n)的确定:模型中对称轴的 分布规律为(图 1-1):①垂直并平分晶棱的假想直 线只能是 L 2;②通过晶面中心且垂直该晶面的假 想直线可能是 L 2、L 3、L 4、L 6;③通过角顶的假 想直线可能是 L 3、L 4、L 6。根据上述对称轴的分 布规律,找出模型中所有的对称轴。注意:L 1 无 实际意义,可以省略。 ⑶找对称中心(C)的确定:在晶体中可没有 对称中心,若有则只能有 1 个,位于晶体几何中 心。对称中心的一般找法为:将模型每一个晶面 分别贴于桌面上,如果都存在跟它反向平行的晶面,则该模型存在对称中心;如果 晶体上部出现棱或角顶,则该模型无对称中心。 ⒊根据对称要素组合定理, 推导出晶体模型中全部对称要素 ⑴ 低级晶族(三斜、单斜、斜方晶系):模型上无高次轴,当找到 L 2 时,将其 直立,再观察: ①有无与其垂直的 L 2,若有则必有 2 个 L 2 同时垂直该 L 2,为 3 L 2(L 2 × L 2 (⊥) → L 2 2L2→3 L 2)。 ②有无包含 L 2 的 P,若有则必有 2 个 P 同时包含该 L 2(L 2 × P(‖) → L 2 2 P)。 ③有无与 L 2 垂直的 P,若有则该模型必有对称中心 C(L 2 +P(⊥)→ L 2PC)。 ⑵中级晶族四方晶系:模型上只有一个高次轴 L 4,当找到 L 4 时,将其直立,再 观察: 图 1-1 立方体中对称轴的分布

①有无与其垂直的L2,若有则必有4个2同时垂直该L,为42(L4×L24 →L44L2)。 ②有无包含L的P,若有则必有4个P同时包含该L4(L4×P,一L4P) ③有无与L垂直的P,若有则该模型必有对称中心C(L+P4)→LPC)。 (3)中级晶族三、六方晶系:在三、六方晶系中,有一个L3(L3,)或5(L5), 它们是通过角顶或面中心的一条假想直线,当找到L或L5时,将其直立,再观察: ①有无与L心(或L5)垂直的2,若有则必有3个L2同时垂直该L3(或6个L 同时垂直该L6): ②有无包含L(或L5)的P,若有则必有3个P同时包含该L(或6个P同时 包含该L5): ③有无与2(或L5)垂直的P,若有则该模型必有对称中心C。 (④高级晶族:在高级晶族中存在一些特殊情况,尽量不用组合定理找对称要素。 高级品族必有三个相互垂直的L或L或L:,如果有3个L相互垂直,在三个 相互垂直的L4的等角度处必有L3,而且有4个L与之斜交,有6个L2分别位于2 个L4的角分线处:若有对称面P存在时,则必有9个对称面和对称中心存在,即对 称型为3L4L26L29PC。如果有3个L2相互垂直,在三个相互垂直的L2的等角度 处必有4个L与之斜交:若有对称面P存在时,则必有3个对称面和对称中心存在, 即对称型为3L24L3PC 4.确定对称型及划分晶族和品系 将所有对称要素按对称轴→对称面一对称中心顺序书写,并在对称轴和对称面 前面加上数目:注意:对称轴一般书写顺序由高到低,如:3L44L6L9PC。但在等轴 品系中有特例:如3L24L3PC。根据有无高次对称轴及高次轴的个数来划分品族: 再根据对称型的特点来划分晶系。 5.进行对称要素的目估极射赤平投影 为了表明对称要素的相互位置关系和进一步研究品体的几何规律,常将品体的 对称要素进行目估投影(极射赤平投影法)。先在纸上画个虚线圆作为基圆(图1-2)。 )对称面的投影:对称面相当于通过品体中心的平面,其投影为一大圆弧,在 投影图上用实线表示。①对称面与投影面平行时,其投影为水平大圆,与基圆重合 (图12b):②对称面上与投影面垂直时,其投影为基圆的直径(图12):③对称面 与投影面斜交时,其投影为一大圆弧(图1-2),需要注意的是与投影面斜交的对称 面只出现在等轴晶系中,且如果有就有4个。 (2)对称轴的投影:对称面相当于通过晶体中心的直线,其投影与直线投影相同, 轴次不同则用不同的符号表示(图1-3)
3 ①有无与其垂直的 L 2,若有则必有 4 个 L 2 同时垂直该 L 4,为 4 L 2(L 4×L 2 (⊥) → L 4 4L2)。 ②有无包含 L 4 的 P,若有则必有 4 个 P 同时包含该 L 4(L 4×P(‖) → L 44P)。 ③有无与 L 4 垂直的 P,若有则该模型必有对称中心 C(L 4+P(⊥)→ L 4PC)。 ⑶中级晶族三、六方晶系:在三、六方晶系中,有一个 L 3(L 3 i)或 L 6(L 6 i), 它们是通过角顶或面中心的一条假想直线,当找到 L 3 或 L 6 时,将其直立,再观察: ①有无与 L 3(或 L 6)垂直的 L 2,若有则必有 3 个 L 2 同时垂直该 L 3(或 6 个 L 2 同时垂直该 L 6); ②有无包含 L 3(或 L 6)的 P,若有则必有 3 个 P 同时包含该 L 3(或 6 个 P 同时 包含该 L 6); ③有无与 L 2(或 L 6)垂直的 P,若有则该模型必有对称中心 C。 ⑷高级晶族:在高级晶族中存在一些特殊情况,尽量不用组合定理找对称要素。 高级晶族必有三个相互垂直的 L 4 或 L 2 或 L 4 i,如果有 3 个 L 4 相互垂直,在三个 相互垂直的 L 4 的等角度处必有 L 3,而且有 4 个 L 3 与之斜交,有 6 个 L 2 分别位于 2 个 L 4 的角分线处;若有对称面 P 存在时,则必有 9 个对称面和对称中心存在,即对 称型为 3 L44 L36 L 29PC。如果有 3 个 L 2 相互垂直,在三个相互垂直的 L 2 的等角度 处必有 4 个 L 3 与之斜交;若有对称面 P 存在时,则必有 3 个对称面和对称中心存在, 即对称型为 3 L24 L33PC。 ⒋ 确定对称型及划分晶族和晶系 将所有对称要素按对称轴→对称面→对称中心顺序书写,并在对称轴和对称面 前面加上数目;注意:对称轴一般书写顺序由高到低,如:3L4 4L36L29PC。但在等轴 晶系中有特例:如 3 L24 L33PC 。根据有无高次对称轴及高次轴的个数来划分晶族; 再根据对称型的特点来划分晶系。 ⒌ 进行对称要素的目估极射赤平投影 为了表明对称要素的相互位置关系和进一步研究晶体的几何规律,常将晶体的 对称要素进行目估投影(极射赤平投影法)。先在纸上画个虚线圆作为基圆(图 1-2a)。 ⑴对称面的投影:对称面相当于通过晶体中心的平面,其投影为一大圆弧,在 投影图上用实线表示。① 对称面与投影面平行时,其投影为水平大圆,与基圆重合 (图 1-2b);②对称面与投影面垂直时,其投影为基圆的直径(图 1-2c); ③对称面 与投影面斜交时,其投影为一大圆弧(图 1-2d),需要注意的是与投影面斜交的对称 面只出现在等轴晶系中,且如果有就有 4 个。 ⑵对称轴的投影:对称面相当于通过晶体中心的直线,其投影与直线投影相同, 轴次不同则用不同的符号表示(图 1-3)
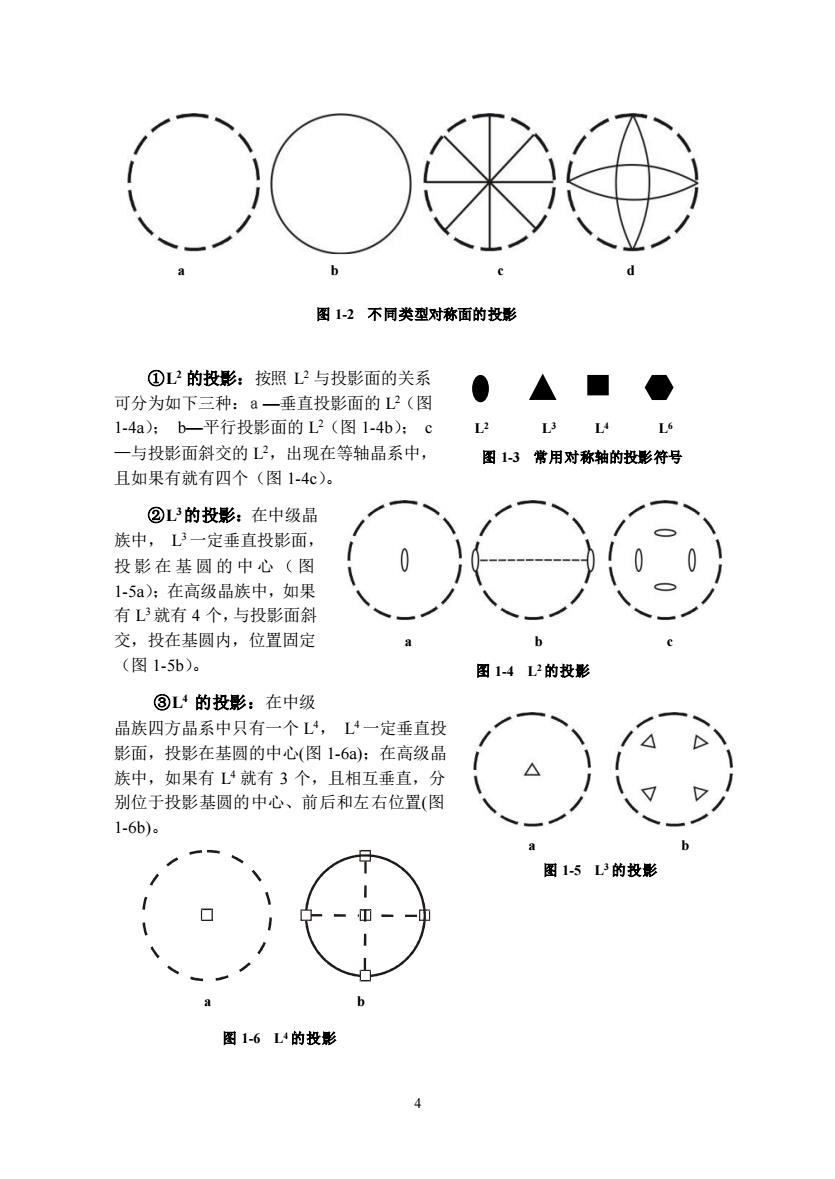
图12不同类型对称面的投影 ①L2的投影:按照L2与投影面的关系 可分为如下三种:日一垂直投影面的L2(图 1-4a):b一平行投影面的L2(图1-4b):c L L 一与投影面斜交的?,出现在等轴品系中, 图13常用对称轴的投影符号 且如果有就有四个(图1-4c)。 ②L的投影:在中级品 族中,L3一定垂直投影面, 投影在基圆的中心(图 1-5a):在高级晶族中,如果 有就有4个,与投影面斜 交,投在基圆内,位置固定 h (图1-5b)。 图14P的投影 ③L的投影:在中级 晶族四方品系中只有一个L,L一定垂直投 影面,投影在基圆的中心(图1-6a):在高级晶 族中,如果有L4就有3个,且相互垂直,分 别位于投影基圆的中心、前后和左右位置(图 1-6b。 图15P的投形彩 6 图1-6L的投影
4 ①L 2 的投影:按照 L 2 与投影面的关系 可分为如下三种:a—垂直投影面的 L 2(图 1-4a); b—平行投影面的 L 2(图 1-4b); c —与投影面斜交的 L 2,出现在等轴晶系中, 且如果有就有四个(图 1-4c)。 ②L 3的投影:在中级晶 族中, L 3 一定垂直投影面, 投影在基圆的中心(图 1-5a);在高级晶族中,如果 有 L 3 就有 4 个,与投影面斜 交,投在基圆内,位置固定 (图 1-5b)。 ③L 4 的投影:在中级 晶族四方晶系中只有一个 L 4, L 4 一定垂直投 影面,投影在基圆的中心(图 1-6a);在高级晶 族中,如果有 L 4 就有 3 个,且相互垂直,分 别位于投影基圆的中心、前后和左右位置(图 1-6b)。 L2 L3 L4 L6 图 1-3 常用对称轴的投影符号 a b c d 图 1-2 不同类型对称面的投影 a b c 图 1-4 L2的投影 a b 图 1-5 L3 的投影 a b 图 1-6 L4的投影

④L5的投影:L6只出现在中 级晶族六方晶系中,投影时L 一定垂直投影面,投影在基圆的中 心(图17)。 (3)对称中心的投影:对称中心 相当于晶体几何中心位置的点,其 图17L的投影 图1-8C的投影 投影在投影图的中心,用“C”表 示(图1-8)。 6.注意事项: ()对于单斜品系应使其维一的P平行投影面且位于左右方向,或使其维一的对 称面的法线方向位于左右方向: (2)斜方品系的品体,应使其2分别位于投影图之中心及左右和前后方向。 (3)中级晶族的高次轴一定垂直投影面,投在基圆中心。 (4)对于等轴晶系则应使其三个相互垂直的L(或L2等)分别位于投影图之中心及 左右和前后方向。 四、实习报告 观察晶体模型,确定其对称型,并完成其对称要素的目估极射赤平投影图: 模型号 对称型 品族 晶系 目估投影图 》
5 ④L 6 的投影:L 6 只出现在中 级晶族六方晶系中, 投影时 L 6 一定垂直投影面,投影在基圆的中 心(图 1-7)。 ⑶对称中心的投影:对称中心 相当于晶体几何中心位置的点,其 投影在投影图的中心,用“C”表 示(图 1-8)。 ⒍ 注意事项: ⑴对于单斜晶系应使其维一的 L 2 平行投影面且位于左右方向,或使其维一的对 称面的法线方向位于左右方向; ⑵斜方晶系的晶体,应使其 L 2 分别位于投影图之中心及左右和前后方向。 ⑶中级晶族的高次轴一定垂直投影面,投在基圆中心。 ⑷对于等轴晶系则应使其三个相互垂直的 L 4 (或 L 2 等)分别位于投影图之中心及 左右和前后方向。 四、实习报告 观察晶体模型,确定其对称型,并完成其对称要素的目估极射赤平投影图: 模型号 对称型 晶族 晶系 目估投影图 图 1-7 L6的投影 图 1-8 C 的投影

实习二晶体定向及目估结晶符号 一。课前准备 通过教材相关内容的学习,了解晶体定向原则和各晶系品体的定向方法及其品 体常数特点。 二.目的要求 1.学会各晶系的晶体定向: 2.在结品模型上确定品面符号: 3.掌握文字符号的表示方法。 4.掌握对称型的国际符号。 三。内容方法和步骤 1.确定晶体模型的对称型及所属晶族、晶系。 2。晶体定向:选择晶轴和确定轴单位。各晶系的选择晶轴原则和晶体常数特征 见教材的表41。要注意三轴晶体和四轴晶体的定向方式及参数特征差异。 3.目估晶面符号:晶面符号采用米氏符号,即将晶面指数用“()”括起来表示 一般写成(hk)。其中晶面指数是晶面在三个结晶轴上截距系数的倒数比,顺序为: X轴、Y轴、Z轴。 晶面符号的确定:①晶面于某一晶轴平行,则对应于该轴的晶面指数为0”: ②晶面与晶轴相截,如果能确定具体数字时,则晶面指数用阿拉伯数字表示,如 (100)、(211)人、(110)等:如果不能确定具体数字时,则晶面指数可用文字符号h k、I表示,如(hk)、(hkk)。③文字符号h、k、I的使用:h、k、I在各晶系的使用 方法各不相同,其中: 等轴晶系一h>k>l,即大的晶面指数用h,其次用k,最小的用1表示。 四方晶系-h>k,1固定代表Z轴的晶面指数。 低级品族一h、k、1分别固定代表X、Y、Z轴的品面指数,如品面与三个结 品轴相截时,品面符号可表示为(hkl)。 注意事项:①文字符号一般不与数字符号混用。如(h20)就是错误的写法:但 (hk0)则可以,它表示该晶面与Z轴平行,与X、Y轴相截,且截距系数比不确切。 ②品面符号应是简单数字。如:(00)、(400)并不是最简单数字,应写成(100):同 样(hh0)、(330)等类似情形也应写成(110)。 4.对称型的国际符号确定:国际符号一般是由不多于三个结品学方位的对称要 素所构成。它们的位置均表示一定的结品学方位。首先根据品体的对称特点,进行 晶体定向。再根据该晶系对称型的国际符号各序位所表示的结晶方位,找出该方位 6
6 实习二 晶体定向及目估结晶符号 一.课前准备 通过教材相关内容的学习,了解晶体定向原则和各晶系晶体的定向方法及其晶 体常数特点。 二.目的要求 1. 学会各晶系的晶体定向; 2. 在结晶模型上确定晶面符号; 3. 掌握文字符号的表示方法。 4. 掌握对称型的国际符号。 三.内容方法和步骤 ⒈ 确定晶体模型的对称型及所属晶族、晶系。 ⒉ 晶体定向:选择晶轴和确定轴单位。各晶系的选择晶轴原则和晶体常数特征 见教材的表 4-1。要注意三轴晶体和四轴晶体的定向方式及参数特征差异。 ⒊ 目估晶面符号:晶面符号采用米氏符号,即将晶面指数用“( )”括起来表示, 一般写成(hkl)。其中晶面指数是晶面在三个结晶轴上截距系数的倒数比,顺序为: X 轴、Y 轴、Z 轴。 晶面符号的确定:①晶面于某一晶轴平行,则对应于该轴的晶面指数为“0”; ②晶面与晶轴相截,如果能确定具体数字时,则晶面指数用阿拉伯数字表示,如 (100)、(211)、(110)等;如果不能确定具体数字时,则晶面指数可用文字符号 h、 k、l 表示,如(hkl)、(hkk)。③文字符号 h、k、l 的使用:h、k、l 在各晶系的使用 方法各不相同,其中: 等轴晶系—h>k>l,即大的晶面指数用 h,其次用 k,最小的用 l 表示。 四方晶系—h>k, l 固定代表 Z 轴的晶面指数。 低级晶族—h、k、l 分别固定代表 X、Y、Z 轴的晶面指数,如晶面与三个结 晶轴相截时,晶面符号可表示为(hkl)。 注意事项:①文字符号一般不与数字符号混用。如(h20)就是错误的写法;但 (hk0)则可以,它表示该晶面与 Z 轴平行,与 X、Y 轴相截,且截距系数比不确切。 ②晶面符号应是简单数字。 如:(h00)、(400)并不是最简单数字,应写成(100);同 样(hh0)、(330)等类似情形也应写成(110)。 ⒋ 对称型的国际符号确定:国际符号一般是由不多于三个结晶学方位的对称要 素所构成。它们的位置均表示一定的结晶学方位。首先根据晶体的对称特点,进行 晶体定向。再根据该晶系对称型的国际符号各序位所表示的结晶方位,找出该方位

存在的对称轴或垂直该方向的对称面。各位置以与该方向平行的对称轴(或旋转反 伸轴)或与该方向垂直的对称面来表示。当对称轴和对称面法线在同一方向上同时 出现时,则二者用斜线或横线隔开,写在同一序位上,如2m(或2)表示2与m 垂直。如果某方位无对称要素出现时,符号中该位置空白。因为国际符号的三个位 置均不等效,因此必须按一定顺序书写,不同晶系的国际符号各位序所表示的结晶 学方位不同。 5.目估极射赤平投影:包括对称要素和各晶面的投影。 举例:萤石晶体棋型 ()对称型为3L4L6L29PC,属高级品族等轴品系。 (②)晶体定向:选3L分别为X、Y、Z轴。判断各个晶面的符号。 (3)对称型的国际符号:m3m。 (④)完成目估投影: 四.实习报告 观察晶体模型,确定其对称型,对晶体进行定向,写出其对称型的国际符号。 最后完成其对称要素的目估极射赤平投影图: 模型号 对称型晶族、晶系 晶体定向方式 国际符号 目估投影图
7 存在的对称轴或垂直该方向的对称面。各位置以与该方向平行的对称轴(或旋转反 伸轴)或与该方向垂直的对称面来表示。当对称轴和对称面法线在同一方向上同时 出现时,则二者用斜线或横线隔开,写在同一序位上,如 2 m (或 m 2 )表示 2 与 m 垂直。如果某方位无对称要素出现时,符号中该位置空白。因为国际符号的三个位 置均不等效,因此必须按一定顺序书写,不同晶系的国际符号各位序所表示的结晶 学方位不同。 ⒌ 目估极射赤平投影:包括对称要素和各晶面的投影。 举例:萤石晶体模型 ⑴对称型为 3L44L36L29PC,属高级晶族等轴晶系。 ⑵晶体定向:选 3L4 分别为 X、Y、Z 轴。判断各个晶面的符号。 ⑶对称型的国际符号:m3m。 ⑷完成目估投影: 四.实习报告 观察晶体模型,确定其对称型,对晶体进行定向,写出其对称型的国际符号。 最后完成其对称要素的目估极射赤平投影图: 模型号 对称型 晶族、晶系 晶体定向方式 国际符号 目估投影图

实习四认识单形 一、课前准备 理解单形概念,了解单形的推导方法及47种单形在各晶系分布的一般规律。 二、目的与要求 1.认识47种几何单形,重点掌握17种常见单形的主要识别特征。 2.掌握常见单形的品面与对称要素之间的相对位置关系。 3.理解几何单形与结晶单形的关系,了解常见单形在各晶系中的分布 三、实习内容 1.认识单形:根据单形的命名原则,对照教材图5-7认识47种几何单形。 单形几何特征的观察内容主要包括如下几个方面:①品面数目:②品面的形状: ③品面间的几何关系:④品面与对称要素间的关系:⑤通过品体中心的横切面形状。 掌握单形要与其所属的晶族、晶系联系起来,有些单形只在特定的晶族、晶系 或晶类中出现。如高级晶族的立方体、八面体、菱形十二面体等15个单形,只能在 等轴品系中出现:四方品系的四方柱、四方双锥等只出现在四方品系中:斜方双锥 只出现在斜方双锥晶类(3L3PC)中。有些几何单形则可以在不同的晶族、晶系或 晶类中出现,如单面和平行双面,在低级晶族和中级晶族的各晶系中均可出现:三 方柱、六方柱、三方双维、六方双锥等单形,即可以在三方品系中出现,又可以在 六方晶系中出现:立方体即可以在六八面体品类中出现,又可以在偏方复十二面体 晶类中出现:但这些在不同晶族、晶系或晶类中出现的相同几何单形,应属于不同 的结晶单形。 2重点掌握17种常见单形的名称:在47种几何单形中,常见的有17种,其主 要几何特征见表3-1。 3.确定单形符号 (1)选取单形中代表晶面(按前、右 上原则): (②)确定代表晶面的晶面指数: (3)确定单形符号一将品面指数用 大括号“{}”括起来。 如萤石的对称型为3L44L6L29PC, 图31萤石晶体及各单形代表晶面投影 其对称要素目估极射赤平投影图和每个 单形的代表晶面投影点见图3-1
8 实习四 认识单形 一、课前准备 理解单形概念,了解单形的推导方法及 47 种单形在各晶系分布的一般规律。 二、目的与要求 ⒈ 认识 47 种几何单形,重点掌握 17 种常见单形的主要识别特征。 ⒉ 掌握常见单形的晶面与对称要素之间的相对位置关系。 ⒊ 理解几何单形与结晶单形的关系,了解常见单形在各晶系中的分布。 三、实习内容 ⒈ 认识单形:根据单形的命名原则,对照教材图 5-7 认识 47 种几何单形。 单形几何特征的观察内容主要包括如下几个方面:①晶面数目;②晶面的形状; ③晶面间的几何关系;④晶面与对称要素间的关系;⑤通过晶体中心的横切面形状。 掌握单形要与其所属的晶族、晶系联系起来,有些单形只在特定的晶族、晶系 或晶类中出现。如高级晶族的立方体、八面体、菱形十二面体等 15 个单形,只能在 等轴晶系中出现;四方晶系的四方柱、四方双锥等只出现在四方晶系中;斜方双锥 只出现在斜方双锥晶类(3L23PC)中。有些几何单形则可以在不同的晶族、晶系或 晶类中出现,如单面和平行双面,在低级晶族和中级晶族的各晶系中均可出现;三 方柱、六方柱、三方双锥、六方双锥等单形,即可以在三方晶系中出现,又可以在 六方晶系中出现;立方体即可以在六八面体晶类中出现,又可以在偏方复十二面体 晶类中出现;但这些在不同晶族、晶系或晶类中出现的相同几何单形,应属于不同 的结晶单形。 ⒉重点掌握 17 种常见单形的名称:在 47 种几何单形中,常见的有 17 种,其主 要几何特征见表 3-1。 ⒊ 确定单形符号 ⑴ 选取单形中代表晶面(按前、右、 上原则); ⑵ 确定代表晶面的晶面指数; ⑶ 确定单形符号—将晶面指数用 大括号“{ }”括起来。 如萤石的对称型为 3L44L36L29PC, 其对称要素目估极射赤平投影图和每个 单形的代表晶面投影点见图 3-1。 图 3-1 萤石晶体及各单形代表晶面投影
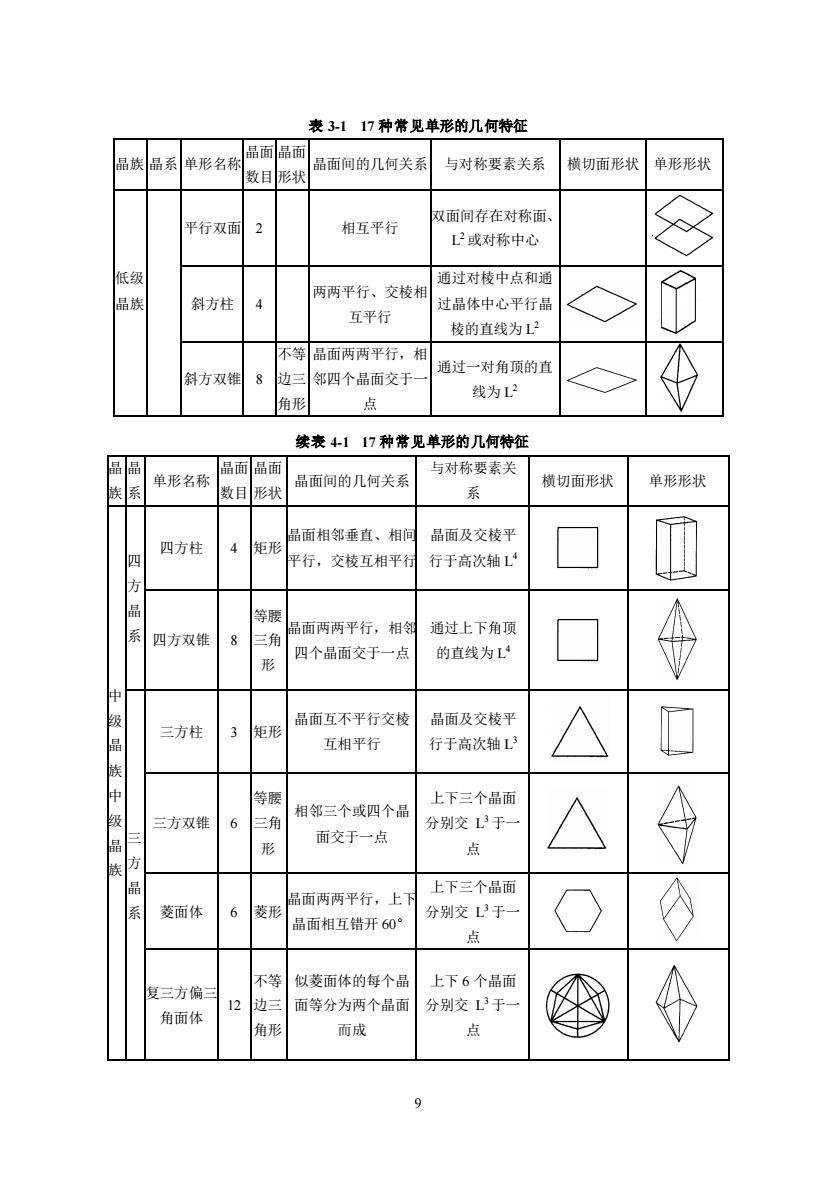
表3117种常见单形的几何特征 品族品系单形名称 品面品面 数目形状 晶面问的几何关系 与对称要素关系 横切面形状单形形状 平行双面 2 相互平行 双面间存在对称面 L或对称中心 通过对棱中点和通 两两平行、交棱相 斜方柱 过品体中心平行品 互平行 棱的直线为L2 不等品面两两平行,相 斜方双 边三 邻四个晶面交于 通过一对角顶的直 角形 线为L2 点 续表4117种誉见单形的几何特行 与对称要素关 单形名 数目形状 品面间的几何关系 横切面形状 单形形状 系 品面相邻垂直、相间 品面及交棱平 四方村 平行,交棱互相平行 行于高次轴 品系 腰 品面两两平行,相 四方双细 角 通过上下角 四个品面交于一点 的直线为L 形 品面互不平行交 中级品族中级品族 晶面及交棱 三方相 3 矩形 互相平行 行于高次轴L 等腰 相邻三个或四个晶 上下三个晶面 三方双细 6 三角 分别交L3于 分 二方 面交于一点 品系 上下三个品面 面两两平行,上 菱面体 6 菱形 分别交L于 品面相互错开60 复三方偏 似菱面体的每个品 上下6个品面 12 角面体 边 面等分为两个晶面 分别交L3于 角形 而成 点 9
9 表 3-1 17 种常见单形的几何特征 晶族 晶系 单形名称 晶面 数目 晶面 形状 晶面间的几何关系 与对称要素关系 横切面形状 单形形状 低级 晶族 平行双面 2 相互平行 双面间存在对称面、 L 2 或对称中心 斜方柱 4 两两平行、交棱相 互平行 通过对棱中点和通 过晶体中心平行晶 棱的直线为 L 2 斜方双锥 8 不等 边三 角形 晶面两两平行,相 邻四个晶面交于一 点 通过一对角顶的直 线为 L 2 续表 4-1 17 种常见单形的几何特征 晶 族 晶 系 单形名称 晶面 数目 晶面 形状 晶面间的几何关系 与对称要素关 系 横切面形状 单形形状 中 级 晶 族 中 级 晶 族 四 方 晶 系 四方柱 4 矩形 晶面相邻垂直、相间 平行,交棱互相平行 晶面及交棱平 行于高次轴 L 4 四方双锥 8 等腰 三角 形 晶面两两平行,相邻 四个晶面交于一点 通过上下角顶 的直线为 L 4 三 方 晶 系 三方柱 3 矩形 晶面互不平行交棱 互相平行 晶面及交棱平 行于高次轴 L 3 三方双锥 6 等腰 三角 形 相邻三个或四个晶 面交于一点 上下三个晶面 分别交 L 3于一 点 菱面体 6 菱形 晶面两两平行,上下 晶面相互错开 60° 上下三个晶面 分别交 L 3于一 点 复三方偏三 角面体 12 不等 边三 角形 似菱面体的每个晶 面等分为两个晶面 而成 上下 6 个晶面 分别交 L 3于一 点
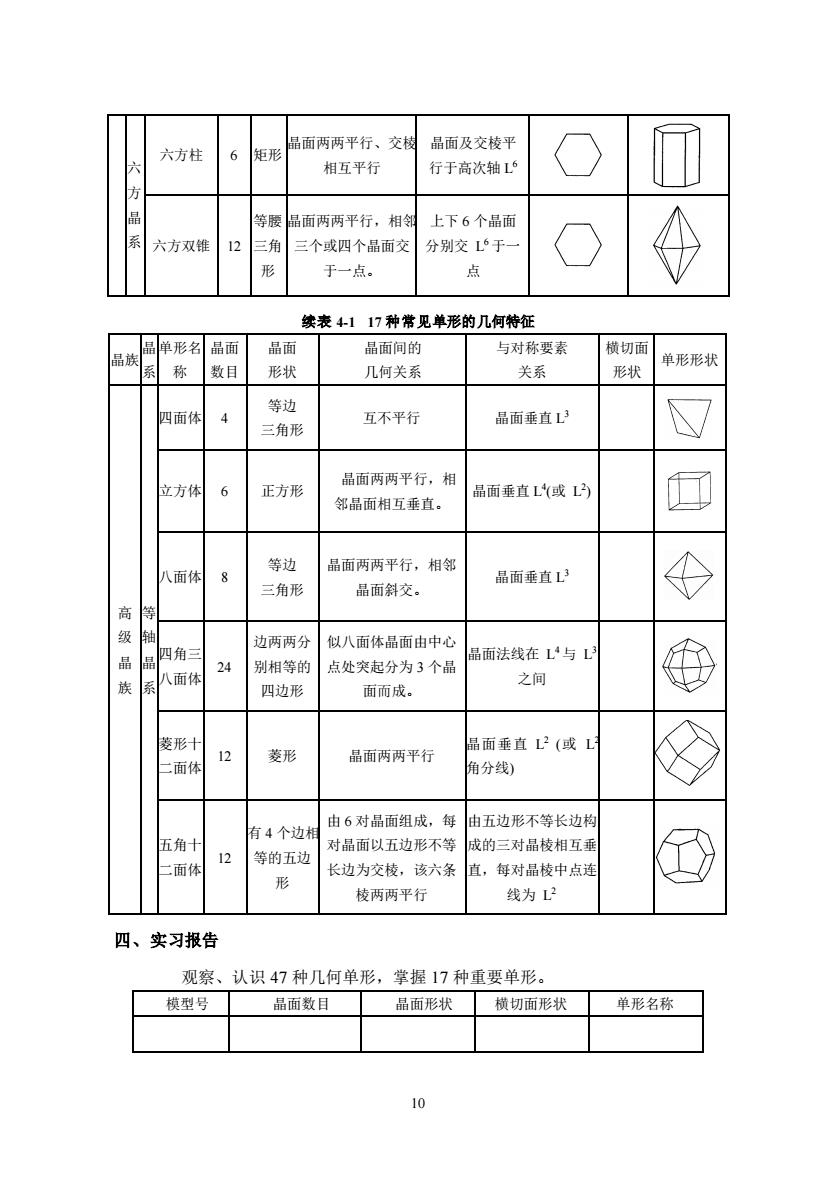
品面两两平行、交 六方柱 晶面及交棱平 6 矩 六 相互平行 行于高次轴L 品系 等腰 品面两两平行,相 上下6个品面 六方双细 12 三角 三个或四个品面交 分别交L于 于一点。 点 续表4117种常见单形的几何特征 晶单形名晶面品面 晶面间的 与对称要素 横切面 系称数日 形状 几何关系 关系 形状 单形形状 等边 四面体 4 三角形 互不平行 晶面垂直L 品面两两平行,相 立方体 6 正方形 邻品面相互垂直。 晶面垂直L(或) 回 等边 晶面两两平行,相邻 八面体 8 三角开 晶面斜交。 晶面垂直 高 边两两分 似八面体品面由中心 品面法线在与L 24 系小八面体 别相等的 点处突起分为3个晶 四边形 面而成。 之间 中 菱形 菱形 品面垂直2(或L 品面两两平行 二面体 角分线) 由6对晶面组成,每由五边形不等长边构 五角 有4个边相 对品面以五边形不等 成的三对品棱相互到 12 等的五边 一面体 长边为交棱,该六条直,每对品棱中点连 棱两两平行 线为2 四、实习报告 观察、认识47种几何单形,掌握17种重要单形。 模型号 品面数目厂 晶面形状横切面形状单形名称 10
10 六 方 晶 系 六方柱 6 矩形 晶面两两平行、交棱 相互平行 晶面及交棱平 行于高次轴 L 6 六方双锥 12 等腰 三角 形 晶面两两平行,相邻 三个或四个晶面交 于一点。 上下 6 个晶面 分别交 L 6于一 点 续表 4-1 17 种常见单形的几何特征 晶族 晶 系 单形名 称 晶面 数目 晶面 形状 晶面间的 几何关系 与对称要素 关系 横切面 形状 单形形状 高 级 晶 族 等 轴 晶 系 四面体 4 等边 三角形 互不平行 晶面垂直 L 3 立方体 6 正方形 晶面两两平行,相 邻晶面相互垂直。 晶面垂直 L 4 (或 L 2 ) 八面体 8 等边 三角形 晶面两两平行,相邻 晶面斜交。 晶面垂直 L 3 四角三 八面体 24 边两两分 别相等的 四边形 似八面体晶面由中心 点处突起分为 3 个晶 面而成。 晶面法线在 L 4与 L 3 之间 菱形十 二面体 12 菱形 晶面两两平行 晶面垂直 L 2 (或 L 2 角分线) 五角十 二面体 12 有 4 个边相 等的五边 形 由 6 对晶面组成,每 对晶面以五边形不等 长边为交棱,该六条 棱两两平行 由五边形不等长边构 成的三对晶棱相互垂 直,每对晶棱中点连 线为 L 2 四、实习报告 观察、认识 47 种几何单形,掌握 17 种重要单形。 模型号 晶面数目 晶面形状 横切面形状 单形名称