
第十章习题课及应用重积分的计算基本概念、i计算方法及应用二、计算方法补充三、 典典型习题HIGH EDUCATION PRESS返回结束机动自录上页下页
习题课 一、 基本概念、计算方法及应用 二、计算方法补充 三、典型习题 机动 目录 上页 下页 返回 结束 第十章 重积分的 计算 及应用

基本概念计算方法及应用一、1.概念与性质二重积分、三重积分HIGH EDUCATION PRESS
一、 基本概念、计算方法及应用 1. 概念与性质 二重积分、三重积分

2.计算法---------化为累次积分直角坐标系:do=dxdy二重积分极坐标系:do=pdpde直角坐标系:dv=dxdydz柱面坐标系:dv=pdpdedz三重积分球面坐标系:dv=rsinpdrdodHIGH EDUCATION PRESS
2. 计算法-化为累次积分 二重积分 三重积分

3.重积分的应用-----几何应用用二重积分:V=f(x,y)doA(1)求立体体积dxdydz用三重积分:V=(2)求曲面面积:用二重积分)2dxdy1+HIGH EDUCATION PRESS
3. 重积分的应用- (1)求立体体积: (2)求曲面面积: )求曲面面积 用二重积分
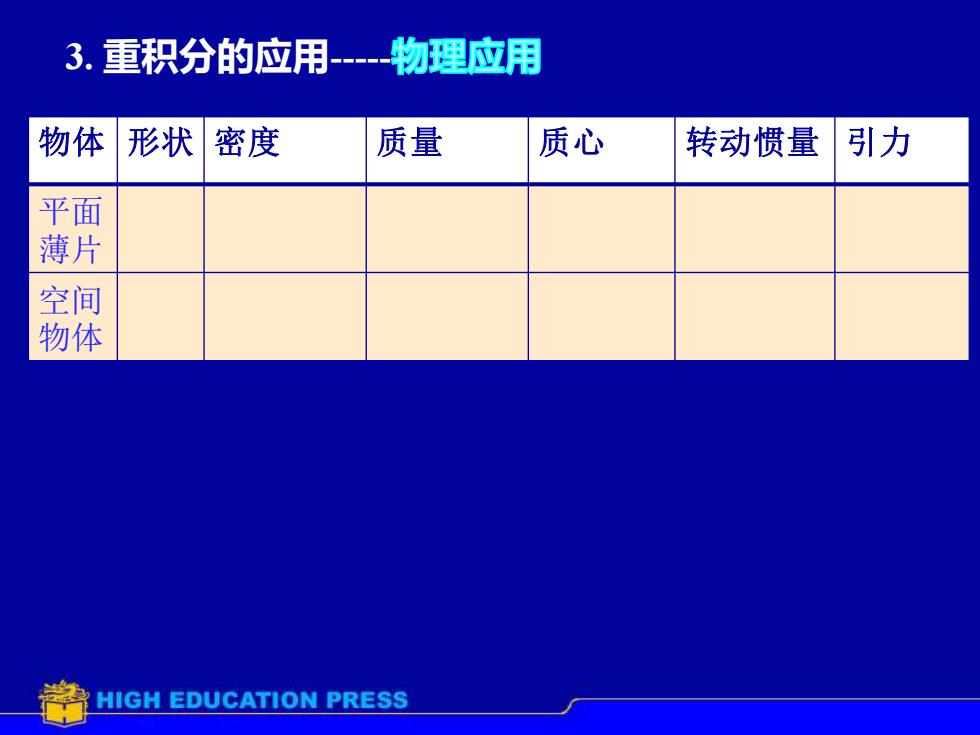
3.重积分的应用-----物理应用物体质量质心引力形状密度转动惯量平面薄片空间物体HIGH EDUCATION PRESS
3. 重积分的应用- 物体 形状 密度 质量 质心 转动惯量 引力 平面 薄片 空间 物体

二、计算方法补充1.交换积分次序计算二重积分例1积分的值为(dyHIGH EDUCATION PRESS
二、 计算方法补充 1. 交换积分次序计算二重积分 例1 积分 的值为( )

例2 设 f(x)为连续函数,F(t)=/dyf(x)dx则F(2)=(D. 0A. 2f(2)B. f(2)C. - f(2)HIGH EDUCATION PRESS
例2 设 为连续函数

sinydxdy,其中D 由抛物线=x例3计算及直线y=x围成。HIGH EDUCATION PRESS
例3 计算 ,其中D 由抛物线 及直线 围成

例4证明dyea-x f(x)dx = (a- x)ea-x f(x)dxHIGH EDUCATION PRESS
例4 证明:

2.利用区域对称性及被积函数的奇偶性简化计算(l)D关于y轴对称,f(x,)是关于x的奇(偶)函数0f(xy)关于x为奇函数[[ f(x,y)do=}2][ f(x,y)do,f(x,y)关于x为偶函数DDHIGH EDUCATION PRESS
2. 利用区域对称性及被积函数的奇偶性简化计算