
第十章第二节二重积分的计算法一、利用直角坐标计算二重积分二、利用极坐标计算二重积分HIGHEDUCATION PRESS返回结束机动自录上页下页
第二节 一、利用直角坐标计算二重积分 二、利用极坐标计算二重积分 机动 目录 上页 下页 返回 结束 二重积分的计算法 第十章

复习:平行截面面积已知的立体体积设所给立体垂直于x车轴的截面面积为A(x),A(x)在[a,b)上连续,则对应于小区间[x,x+dx]的体积元素为dV = A(x)dx因此所求立体体积为7A(x)d xA(x)xx+dxabxHIGH EDUCATION PRESS机动目录上页返回结束下页
复习:平行截面面积已知的立体体积 设所给立体垂直于x 轴的截面面积为A(x), 则对应于小区间 的体积元素为 dV = A(x)d x 因此所求立体体积为 V A x x b a ( )d = 机动 目录 上页 下页 返回 结束 a x b x A(x) 上连续

一、利用直角坐标计算二重积分J f(x, y)dof(x,y)≥0, (x,y)EDy=Φ2(x)a≤x≤bX-型区域D:其中D=qi(x)P(x)≤y≤P2(x)b x则『f(x,y)d 表示曲顶柱体的体积 1Dbxa0HIGH EDUCATION PRESS
一、利用直角坐标计算二重积分 其中 则 表示曲顶柱体的体积 V

计算曲顶柱体体积y=P2(x)任取 xo E[α,b],平面 x= xo截柱体的92(x0)截面积为A(xo)=f(xo, y)dyJo,(xo)xo bxa故曲顶柱体体积为y=@i(x)rTA(x)d xI/ f(x,y)do =arP2(x)f(x,y)dy Jd xJpi(x)[92(x)f(x,y)dydxPi(x)q-HIGH EDUCATION PRESS上页下页返回结束机动自录
x b a [ ]d = 任取 平面 故曲顶柱体体积为 截面积为 f x y y x x ( , )d ( ) ( ) 2 1 = b a A(x)d x 截柱体的 ( ) 2 y = x ( ) 1 y = x z x y o a x0 b D 机动 目录 上页 下页 返回 结束 d b a = x f x y y x x ( , )d ( ) ( ) 2 1

a<x<bX-型区域y=(P2(x)(x)≤y≤P,(x)Dy= i(x)bxOaf(x,y)d可化为二次定积分计算:二重积分DP2(x) f(x, y)do =f(x,y)dy先y后xoxDHIGH EDUCATION PRESS
二重积分 可化为二次定积分计算:

xyd,其中D 是直线y=1, x=2,及例1计算ID所围的闭区域y=x1≤x≤2解:D为X-型区域D(1≤y≤xdxj xydy原式=2 x"[1xy?dx'[1x3-1x]dx8HIGH EDUCATION PRESS
例1 计算 ,其中D 是直线 y=1, x=2, 及 y=x 所围的闭区域. 解: D为X–型区域, 原式=
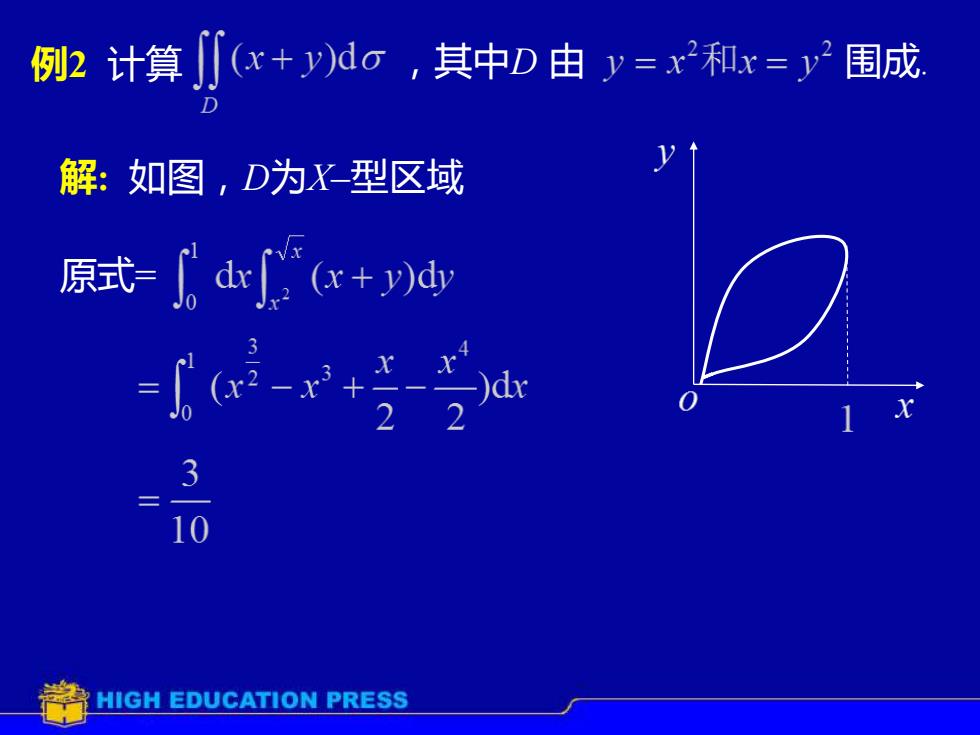
(x+)d,其中D由=x2和x=2围成计算例2D解:如图,D为X-型区域原式=(x+y)dydx10HIGH EDUCATION PRESS
例2 计算 ,其中D 由 围成. 解: 如图,D为X–型区域 原式=

xyd,其中D 是抛物线2=x 及直线例3计算Dy=x-2 所围成的闭区域=x22中Dry=x-2HIGH EDUCATION PRESS
例3 计算 ,其中D 是抛物线 所围成的闭区域. 及直线

V)≤x≤y2()Y-型区域cdx=V2(y)x =Vi((y)Xf(x,y)do可化为二次定积分计算二重积分DW2(y)[ f(x,y)da=先x后yf(x, y)dxDHIGH EDUCATION PRESS机动上页下页返回结束自录
y d c o x ( ) 2 x = y ( ) 1 x = y 机动 目录 上页 下页 返回 结束 二重积分 可化为二次定积分计算:

xyd,其中D 是抛物线2=x 及直线1例3计算Dy=x-2 所围成的闭区域解:为计算简便,先对x后对y积分Dy"≤x≤y+2则 D:x(-1≤y≤2y=x-2J+2xydo ='dy]2 xydx[1x],+2 dy=,v(y+2)? - ]dy458HIGH EDUCATION PRESS目录上页下页返回结束机动
例3 计算 ,其中D 是抛物线 所围成的闭区域. 解: 为计算简便, 先对 x 后对 y 积分, D : xy d x − = 2 1 dy − + = 2 1 2 2 2 1 x y 2 dy y y − = + − 2 1 2 5 [ ( 2) ] d 2 1 y y y y D y = x 2 y = x − 2 2 −1 o y x 2 2 y x y + −1 y 2 2 y y + 2 及直线 则 机动 目录 上页 下页 返回 结束