
第十一章第三节格林公式及其应用格林公式二平面上曲线积分与路径无关的条件三、二元函数的全微分求积四*、全微分方程HIGH EDUCATION PRESS
第三节 一、格林公式 二、平面上曲线积分与路径无关的条件 格林公式及其应用 第十一章 三、二元函数的全微分求积 四*、全微分方程

补充知识:区域“洞”单连通区域(无1.区域D分类“洞区域多连通区域(有内部靠左2.平面区域D的边界曲线L的正向HIGH EDUCATION PRESS
1. 区域 D 分类 单连通区域 ( 无“洞”区域 ) 多连通区域 ( 有“洞”区域 ) 2. 平面区域 D 的边界曲线L 的正向: 内部靠左 补充知识: D D L

格林公式一定理1.设闭区域D由分段光滑的曲线L围成,函数P(x,Jy),Q(x,y) 在 D 上具有连续一阶偏导数,则有apCdxdy=ΦPdx+Qdy(格林公式新其中L是D的取正向的边界曲线HIGH EDUCATION PRESS
定理1. 设闭区域 D 由分段光滑的曲线 L 围成,函数 ( 格林公式 ) 在 D 上具有连续一阶偏导数,则有 一、格林公式 其中L是D的取正向的边界曲线

证明:若D既是X-型区域,又是 Y-型区域,设1:VEPi(x)≤ y≤P2(x)Da≤x≤bDBAap192(x)apY则Jro高dxdxdydy2oy(x)aOyeab x0[P(x, P2 (x)) - P(x, 9(x)]dx而0Pdx=PdxPdx+JLJACBBEAJ.bP(x,P2(x))dxP(x,9(x))]dx +.b[P(x, P(x)-P(x,P2(x)]dxHIGH EDUCATION PRESS目录上页返回结束定理1下页
证明: 1) 若D 既是 X - 型区域 , 又是 Y - 型区域 , 设 a x b x y x D ( ) ( ) : 1 2 则 d c y o x E C A B a b D 定理1 目录 上页 下页 返回 结束 而

2dxdy = Pdx即RQ同理可证dxdy = f, OdyOx②两式相加得1)(%-%)人?dxdy=$ Pdx +Qdy3HIGH EDUCATION PRESS定理1目录返回上页下页结束
即 同理可证 ① ② ①、②两式相加得: 定理1 目录 上页 下页 返回 结束

若D不满足以上条件则可通过加辅助线将其分割2为有限个上述形式的区域,如图IDHLDnXHIGH EDUCATION PRESS定理1目录返回上页下页结束
y o x L 2) 若D不满足以上条件, 则可通过加辅助线将其分割 D1 Dn D2 为有限个上述形式的区域 , 如图 定理1 目录 上页 下页 返回 结束
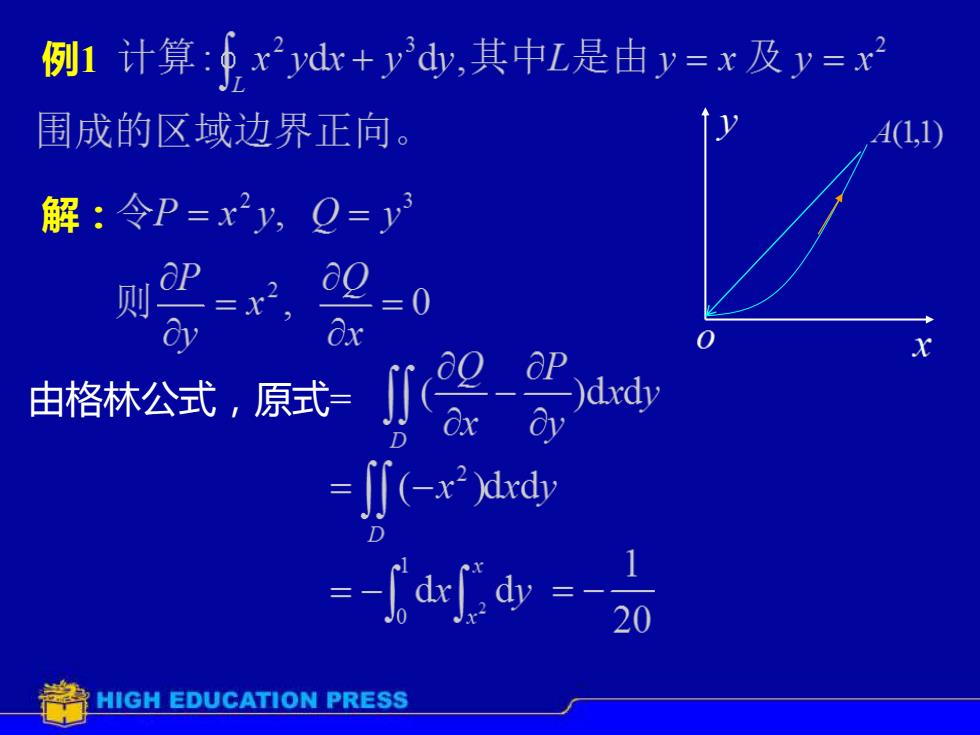
例1计算:xydx+dy,其中L是由=x及=x围成的区域边界正向A(1,1)解:令P=xy,Q=yapaQ则CoydXxapag1)dxdy由格林公式,原式axOyD= Jf(-x)dxdy20HIGH EDUCATION PRESS
例1 解: 由格林公式,原式=

edxdy,其中D 是以 O(0,0),A(1,1),例2. 计算DB(0,1)为顶点的三角形闭域Q= xe-y2,则解: 令P=0,A(1,1)apB(0,1)OxdyDy=x利用格林公式,有xdxdyxedyxeAHIGH EDUCATION PRESS返回结束机动目录上页下页
例2. 计算 ,其中D 是以 O(0,0) , A(1,1) , B(0,1) 为顶点的三角形闭域 . 解: 令 , 则 2 0, y P Q xe − = = 利用格林公式 , 有 x e y OA y d 2 − = ye y y d 1 0 2 − = (1 ) 2 1 −1 = − e y = x o y x A(1,1) B(0,1) D 机动 目录 上页 下页 返回 结束

-0%oQdxdy=dPdx+Qdy格林公式的应用:ax1.利用二重积分计算曲线积分(注意条件)(1)L为闭曲线正向:aPag(2)在D上连续。ax2.求平面区域的面积正向闭曲线L所围区域D的面积xdy-ydxHIGH EDUCATION PRESS
格林公式的应用: 1. 利用二重积分计算曲线积分(注意条件) 2. 求平面区域的面积

x=acosa0≤0≤2元例3 求椭圆所围面积1y=bsine解:xdy-ydx(abcos? +absin?)d=元abHIGH EDUCATION PRESS定理1目录返回上页下页结束
例3 求椭圆 , 0 2 sin cos : = = y b x a L 所围面积 = + 2 0 2 2 ( cos sin )d 2 1 ab ab = ab 定理1 目录 上页 下页 返回 结束 解: