
《测试信号分析与处理》课程 第四章离散傅里叶变换及其 快速算法 第一节序列的傅里叶变换 第二节离散傅里叶级数(DFS) 第三节离散傅里叶变换(DFT) 第四节离散傅里叶变换的性质

《测试信号分析与处理》课程 第五节快速傅里叶变换 第六节IDFT的快速算法(IFFT) 第七节实序列的FFT高效算法 第八节频率域采样理论

第一节序列的傅里叶变换 如X(Z)在单位圆上是收敛的,则将在单位圆上的z 变换定义为序列的傅里叶变换,即 X(a))xnom ÷非周期序列的傅里叶变换"《频谱)的特点在于它是 2周期为2π的连续周期函数,其周期为 ↑x(n) x(e)
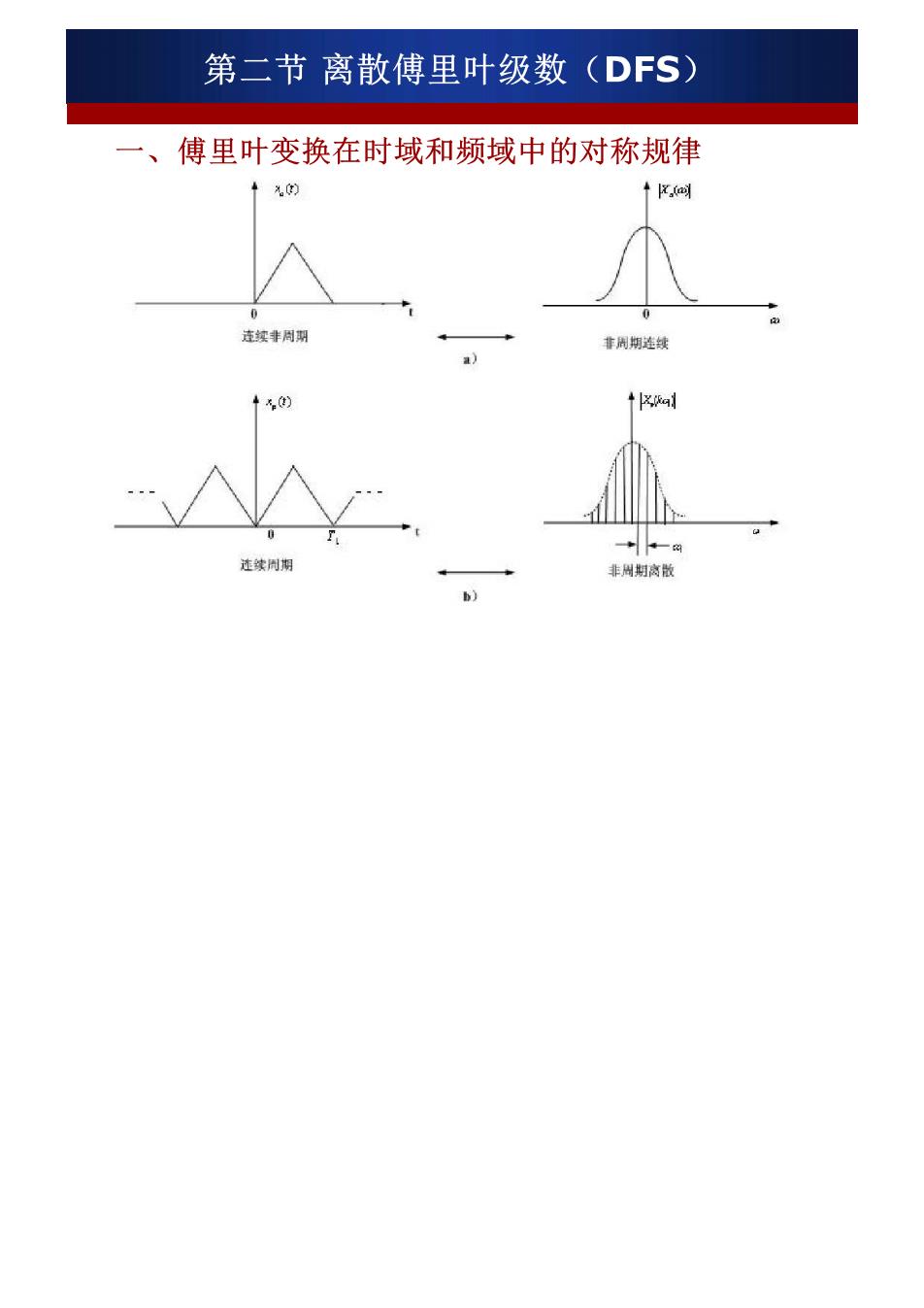
第二节离散傅里叶级数(DFS) 、 傅里叶变换在时域和频域中的对称规律 ↑K同 非周期连域

第二节离散傅里叶级数(DFS) a(nr)n ↑以-渊e 离非周 周期志缓 X,小)

第二节离散傅里叶级数(DFS) 一个域中(时域或频域)是连续的,对应另一个域 中(频域或时域)是非周期的。 一个域中(时域或频域)是离散的,对应另一个域 中(频域或时域)是周期的

第二节离散傅里叶级数(DFS) 二、 离散傅里叶级数 离散周期信号的频谱,即离散傅里叶级数(DFS)。 离散傅里叶级数的变换对表达式 X,=DF,6-2,0wm 1岁X,w x,m=1DFSX,]=N之 所wsey

第三节离散傅里叶变换(DFT) 一、 离散傅里叶变换DFT定义式 必离散傅里叶变换就是对有限长序列进行傅里叶变换 的表示式。 x.(n),0≤n≤N-1 x(n)= 0 ,其他 正变换X(k)=DFT[x(n)]=∑x(n)W n=0 反变换x(n)=IDFT[X(k】= xkw, NK-0
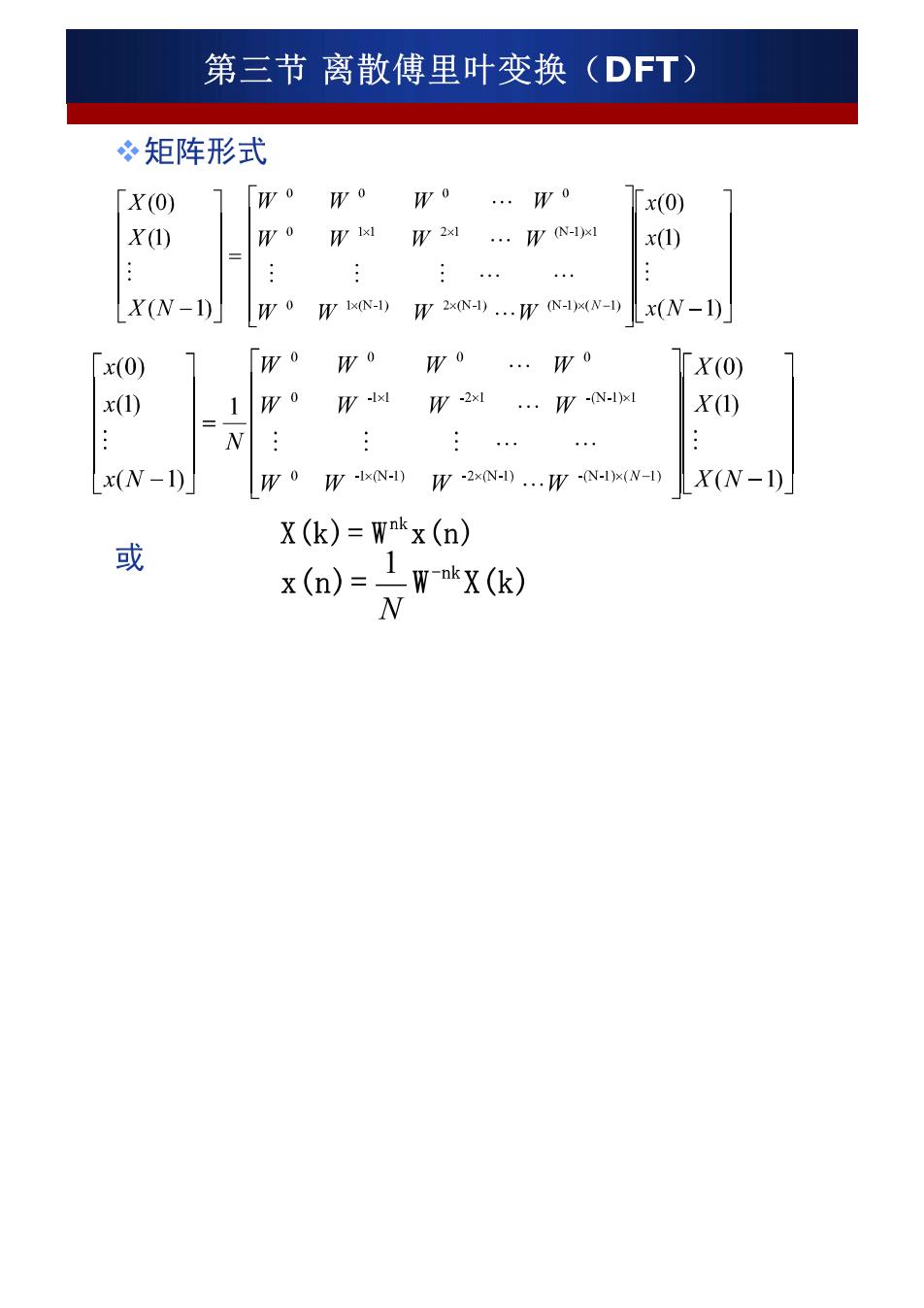
第三节离散傅里叶变换(DFT) 矩阵形式 「X(O) w o x(0) X①) W1W21…WN x(1) … X(N-1) W0p)W2…mN-Lx(N-I) x(0) W0 X(O) x(1) W0W1W2…WN X(1) x(N-1) W o W-Ix(N-1)W-2x(N-1)...W-(N-I(N-1) X(N-1) X(k)=Wmkx(n) 或 x0=为x)

第三节离散傅里叶变换(DFT) 二、DFT的物理意义 有限长序列的DFT就是序列在单位圆上的Z变换(即 有限长序列的傅里叶变换或频谱)以2=2π/为间 隔的抽样值 X(e) X() 元 2元