
第八章随机信号处理 8.1 随机信号的基本概念 8.2 随机信号的描述 8.3 随机信号通过线性系统的分析 8.4 功率谱估计

内容提要 。随着现代测试技术的广泛应用,测试对象和参数 也日益复杂,愈来愈多地涉及到随机信号分析与 处理的知识。本章主要介绍随机信号的基本概念 随机信号的相关分析和谱分析、线性非移变系统 对随机信号的响应、功率谱估计等

第一节随机信号的基本概念 冬公第一章的信号分类中我们已经知道, 随机信号 种不确定性信号,不能表示为二确定的时间 晨数,即信号的变心不存在任阿确定的规裤) 而不可能损见其未来任二时刻的数值,也就是说 它是一种在相同试验条件下,不能重复出现的信 、显然,它与确定性信号是两类性质完全不同 的信号,对随机信等的描述、分析和处理方法也 完全不同于确定性信号。 ·随机信号在客观实际中普遍存在,在测试过程中 也相当常见。例如:陀螺的漂移、测试系统中电 清奇树振的改及试华韵抗奖起 都可以抽象为随机信号。图8-1为某船舶在航行中 所产生的振动信号,这是 一种典型的随机信号
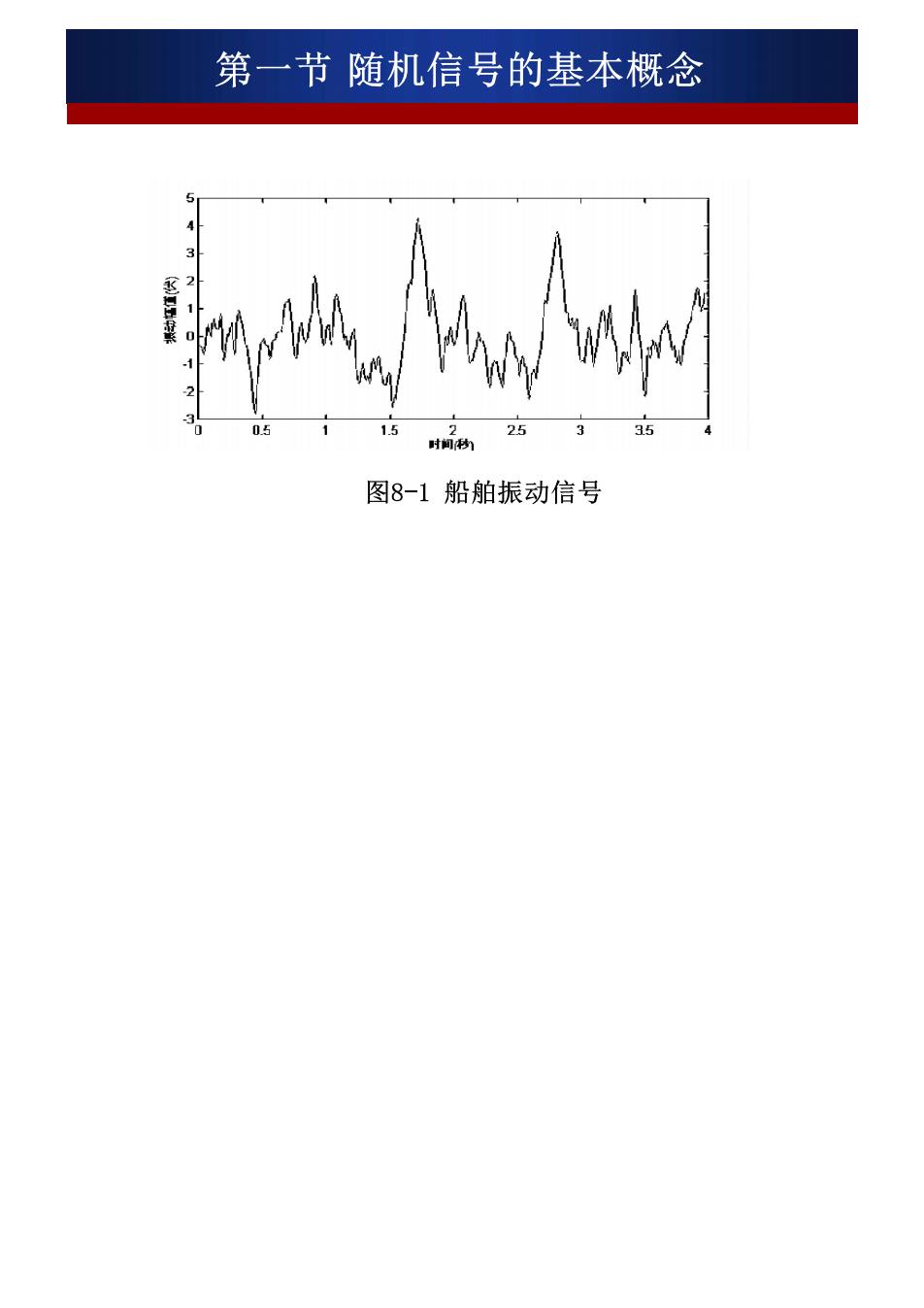
第一节随机信号的基本概念 15 25 3 图8-1船舶振动信号

第一节随机信号的基本概念 仅在离散时间点上给出定义的为离散时间随机信 号,即随机序列。随机序列可以是连续随机信号 的采样结果,也可以是客观存在的随机物理现象 的表示。 对随机物理现象每次的观察结果都不一样,每次 观察得到的时间函数只是可能产生的无限个时间 函数中的一个“样本”,随机现象可能产生的全 部样本的集合(总体)称为随机过程,随机信号 实际上也就是随机过程

第一节随机信号的基本概念 在分析随机信号中由于它的不可重复性,似乎应 当分析无限长的信号才能得到准确的分析结果, 然而这在实际工作中是不可能做到的。对随机信 号的分析只能限定于下面所描述的平稳且各态历 经的随机过程。这类信号便于研究,同时具有普 遍性。 如果随机过程的统计规律不随时间而改变,则称 为平稳随机过程,否则称为非平稳随机过程。 若一个随机过程在某一时刻的所有样本的统计特 征和单一样本在长时间内的统计特征一致,则称 为各态历经(或各态遍历)的随机过程,否则是 非各态历经的随机过程

第一节随机信号的基本概念 www.seu.edu.cn 对于平稳的各态历经的随机过程,从总体各样本 中所能获得的信息并不比从单个样本获得的信息 多,因此在实际应用中,只要对一个样本进行分 析计算,就可以得知随机过程的统计特征。 与确定性信号相比,随机信号有三个主要特点: 1)随机信号的任何一个实现,都只是随机信号总 体中的一个样本,任何一个样本都不能代表该随 机信号

第一节随机信号的基本概念 2)在任一时间点上随机信号的取值都是一个随机 变量,从而随机信号的描述与随机变量一样,只 能用概率密度函数和数学期望这样的数字特征值 来描述。若是各态历经的随机信号,那么数学期 望可用一个样本的时间平均来代替。 3)平稳随机信号在时间上是无始无终的,其能量 是无限的,且不存在傅里叶变换,因此平稳随机 信号不能用通常的频谱来表示,也不能采用常规 的滤波方法进行处理,而需要用基于最小估计理 论的广义滤波一维纳滤波、卡尔曼滤波和自适 应滤波来实现。另外由于随机信号能量是无限的 平均功率是有限的,所以采用功率谱来描述随机 信号的频域特性。 三w

第二节随机信号的描述 由于随机信号不能用确定的时间函数来表示,因 此随机信号只能用其统计特性来描述,一般采用 四种统计特征量来描述其基本特点:①均值(数 学期望)、均方值和方差;②概率密度函数和概 率分布函数;③相关函数和协方差;④功率谱密 度

主要内容 均值、均方值、方差 概率密度函数和概率分布函数 相关函数和协方差 功率谱密度 白噪声和有色噪声信号