
《测试信号分析与处理》课程 第三章离散时间序列及其Z变换 第一节离散时间系统 第二节离散时间信号序列 第三节Z正变换 第四节Z反变换 第五节Z变换的性质 第六节Z变换与拉普拉斯变换的关系 第七节离散信号的Z变换

第一节离散时间系统 一、 离散系统的定义 离散(时间)系统是指输入输出都是时间序列 的系统。 二、离散系统的分类 线性离散系统和非线性离散系统 时不变离散系统和时变离散系统 稳定离散系统和非稳定离散系统 因果系统和非因果系统
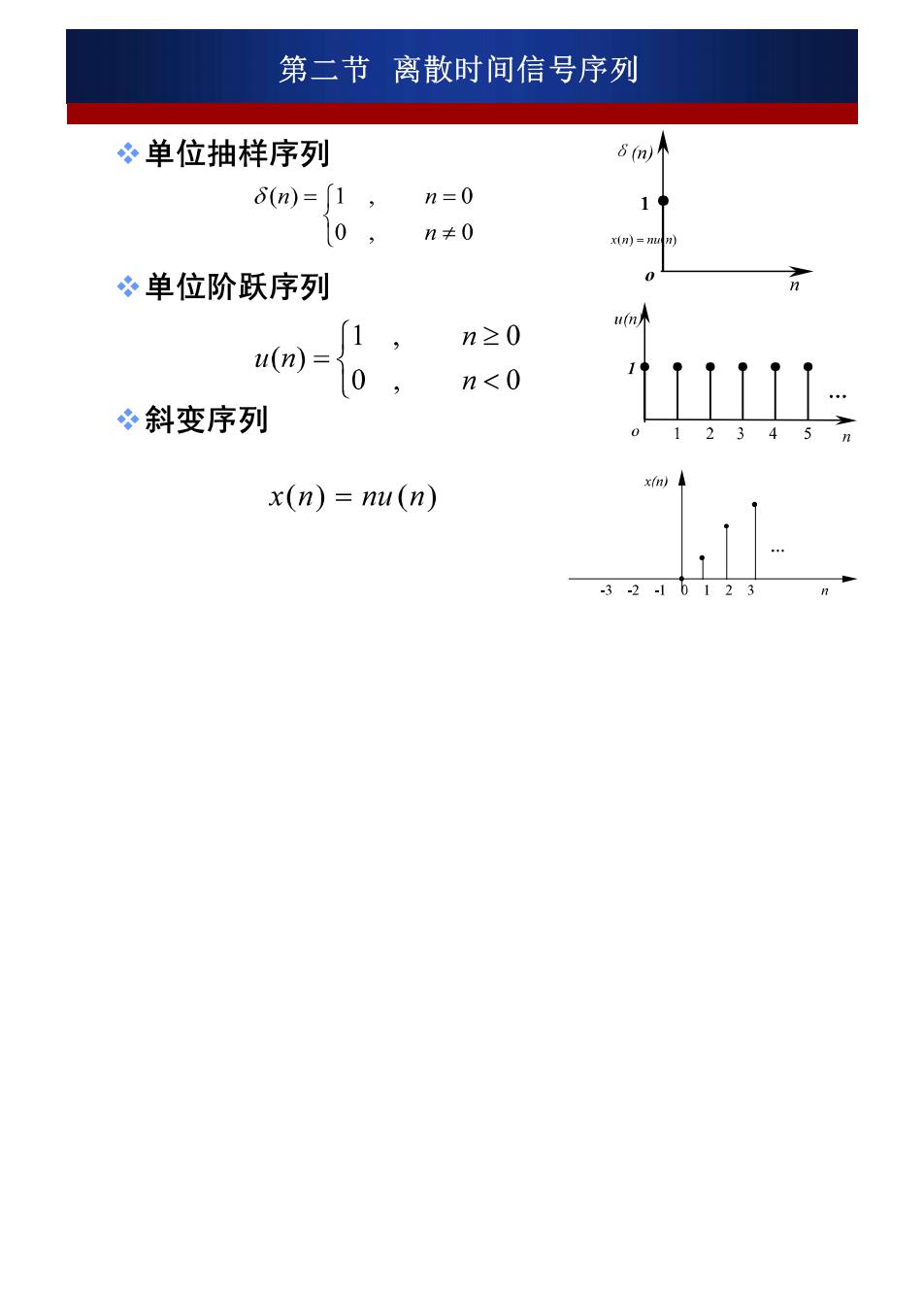
第二节离散时间信号序列 单位抽样序列 6(n)=〔1,n=0 0, n≠0 冬单位阶跃序列 (1, u(n =0, n≥0 n<0 必斜变序列 1234 x(n)=nu(n)
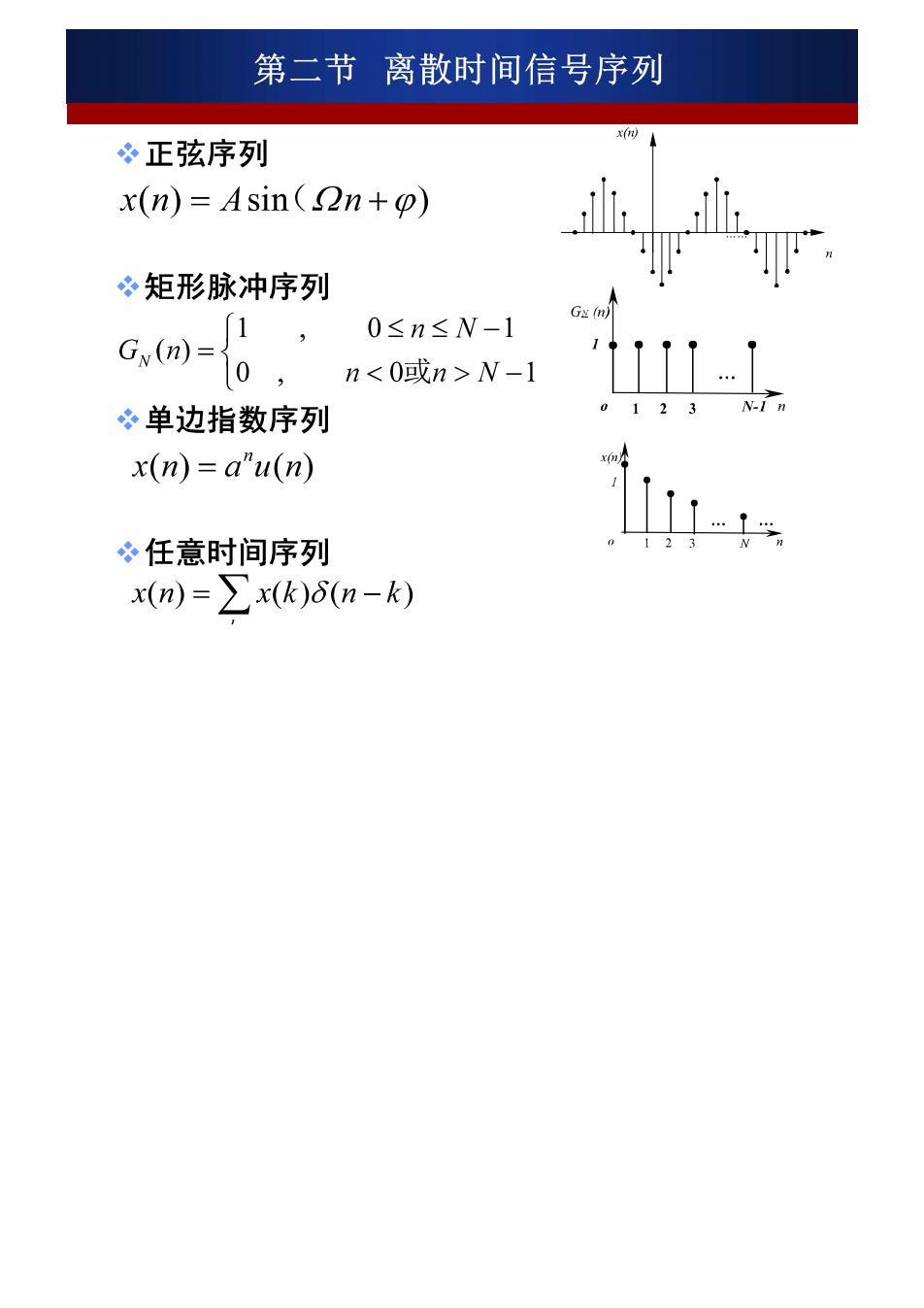
第二节离散时间信号序列 冬正弦序列 x(n)=Asin(2n+o) 冬矩形脉冲序列 1 0≤n≤N-1 Gy (n)= 0, nN-1 1- 单边指数序列 12 x(n)=a"u(n) 任意时间序列 - x(m)=∑x(k)8n-k)

第二节离散时间信号序列 二、序列的基本运算 序列加减 x(n)±y(n)={x(0)±y(0)x(I)±y(I),x(2)±y(2),, x(n)±y(n),} 必序列相乘 x(n)y(n)={x(0)y(0),x(1)y(1),x(2)y(2),,x(n)y(n),} 必序列权乘 a{x(n)}={ax(n)}={ax(0),a.x(1),ax(2),…ax(n),}

第二节离散时间信号序列 序列延时:对序列进行一定的移位。可以表示为 y(n)=x(n-no) 序列折叠:将原序列以纵轴为对称轴进行折叠 y(n)=x(-n) 序列卷积(离散卷积或卷积和)表征了系统响应 y(n)与激励x()和单位冲激响应h(n)的关系。 + y(n)=x(n)*h(n)= ∑x(m)h(n-m) m=-0

第二节离散时间信号序列 卷积和性质 交换律 y(n)=x(n)h(n)=h(n)*x(n) 必结合律 y(n)=[x(n)*h,(n)]*h2(n)=x(n)*[h,(n)*h2(n)] 冬分配律 y(n)=x(n)*[h,(n)+h2(n)]=x(n)*h(n)+x(n)*h2(n)

第二节离散时间信号序列 冬序列相关 互相关函数,(m)=艺xy+m) 自相关函数5,(m)=) .x(n)x(n+m) 冬序列相关性质 1)若xn)是实信号,则r,m)为实偶函数 若x(n)是复信号,则r(m)与:-m)对应序列互为 共 2)r,(m)在m=0达到最大值 3)若x(n)是能量有限信号,当m趋于无穷时,有 lim r,(m)=0

第三节Z正变换 一、Z变换的定义 冬双边Z变换 x()=z[(m)]=x(m) 》单边Z变换 X(2)=Z[x(n)u(n)]=>x(n)z-" 在实际中的离散系统都是因果系统,因此它对应的 Z变换为单边Z变换

第三节Z正变换 我们也可以从拉普拉斯变换导出Z变换 X(s)=5 x(nT,)e-"di=x(nT,)6(t-nT,)e-"dr 三xn)了s-n7e"h-立xa7e听=Xe) 2=est,e(a+io)t,=eoT,ejoT