
《测试信号分析与处理》课程 第二章连续时间信号分析 第一节周期信号分析 第二节非周期信号的频域分析 第三节周期信号的傅里叶变换 第四节采样信号分析

第一节周期信号分析 信号分析就是要研究信号如何表示为各分量的叠 加,并从信号分量的组成情况去考察信号的特性 只要知道周期信号在一个周期内的特性,也就可 以了解到它所具有的全部特性。所以,对周期信 号的研究往往是在一个周期内进行

第一节周期信号分析 一个信号也可以对于某一基函数集找出此信号在 各基函数中的分量; 一个基函数集即可构成一个信号空间,常用的则 是正交函数集。 ”从数学上可以证明,任何一个连续函数都可以在 定义域里用某个正交函数集来表示。 “若此函数集不仅是正交而且完备,则用他来表示 信号时将没有误差

第一节周期信号分析 (一)用完备正交实变函数集来分解信号 函数f(t)与g(t)在区间[G,6,]上正交的条件是 ∫2f0guh=0 例2-1在[0≤t≤2π/o,]内,sino,t与c0sω,t 是正交的。 冬两个函数是否正交,必须指明在什么区间内

第一节周期信号分析 (二)用完备正交复变函数集来分解信号 复变函数集{g,(t),r=1,2,..,n}在区间t,t2J 上是正交函数集的条件是 ∫g,0g0dt=∫gi0g,0dt= 0,i≠j k,i=i 例2-2若0,=2π/T1,在G,4+I]内,指数函 数集{em,n=0,±l,±2,,±oo}是正交函数集。 证明: o(e T,n=m 三角函数集和指数函数集是应用最广的完备正交集

第一节周期信号分析 、 三角函数形式的傅里叶级数 用完备正交函数集{1,cosn@,t,sin no t,n=1,2,3,:…,∞} 对周期信号分解,即可得到周期信号的傅里叶展开式。 进行傅立叶展开的周期函数f(t)必须满足狄里赫利 (irichlet)条件,即在周期,4+T】内,函数 f (t) 1)若有间断点存在,则间断点数目必须有限; 2)极大值和极小值数目应该是有限个; 3》应是绝对可积的,即∫Ft< 在工程实践中所遇到的周期信号一般都满足狄里赫利条 件

第一节周期信号分析 周期信号f)的三角级数形式的傅立叶展开式 f(1)=ao a cos@t+a,cos 2@t+...+b sin t+b,sin 20 t+... =d+(d,cosnon+b,sin non) (≤t≤t+T 其中, 14f0d f(t)cosnotdt (n=1,2,3,…,o) f(t)sin notdt
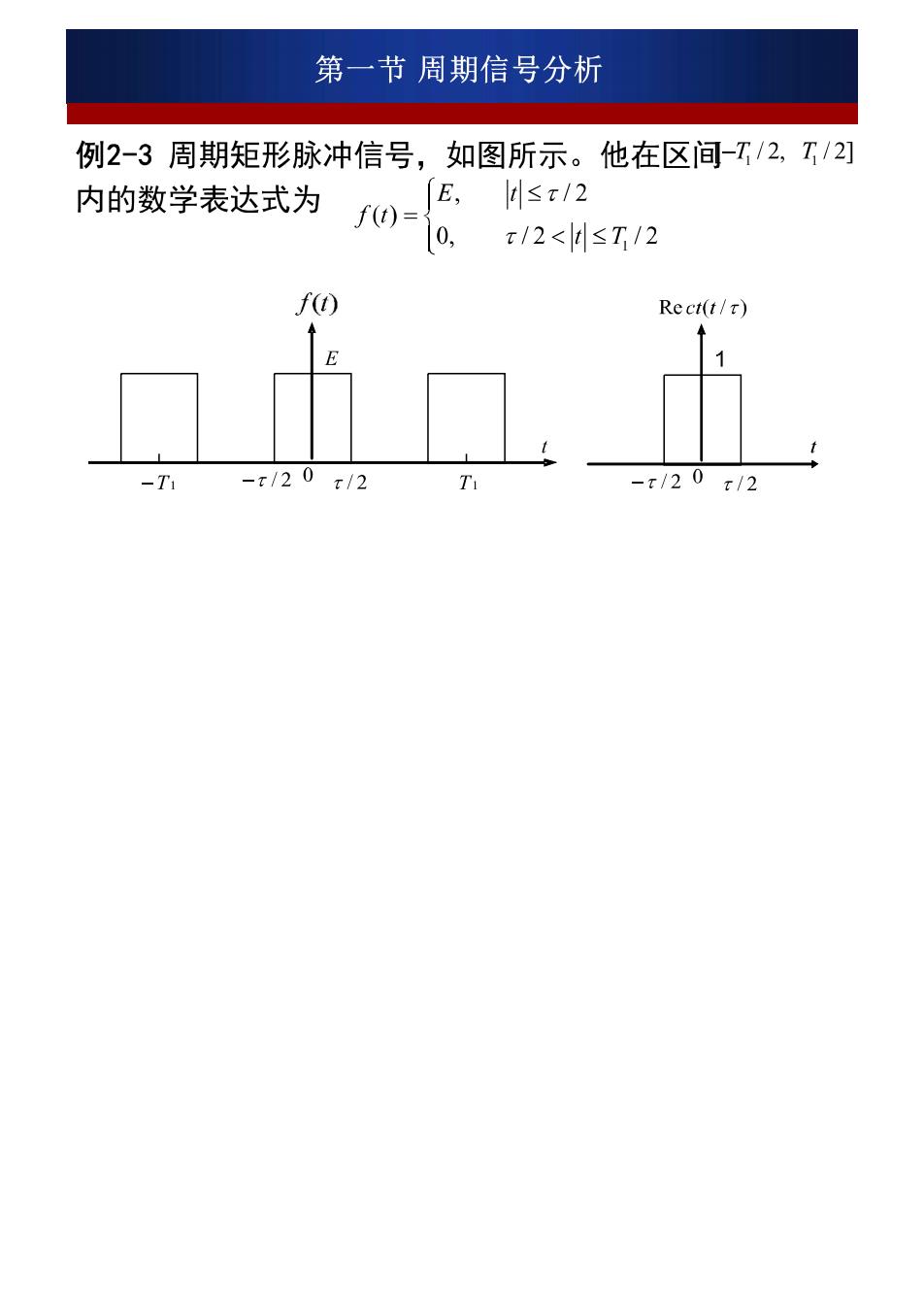
第一节周期信号分析 例2-3周期矩形脉冲信号,如图所示。他在区间-T/2,T/2] 内的数学表达式为f0 E,≤x/2 10, x/2<≤T/2 f() Rect(t/r) -/20x/2 T -x/20r/2

第一节周期信号分析 二、指数函数形式的傅里叶级数 在,4+T]内可以用指数函数集来表示周期信号f(t)。 f0=∑Fa)em:i≤1≤i+T 式中 F(n@)=
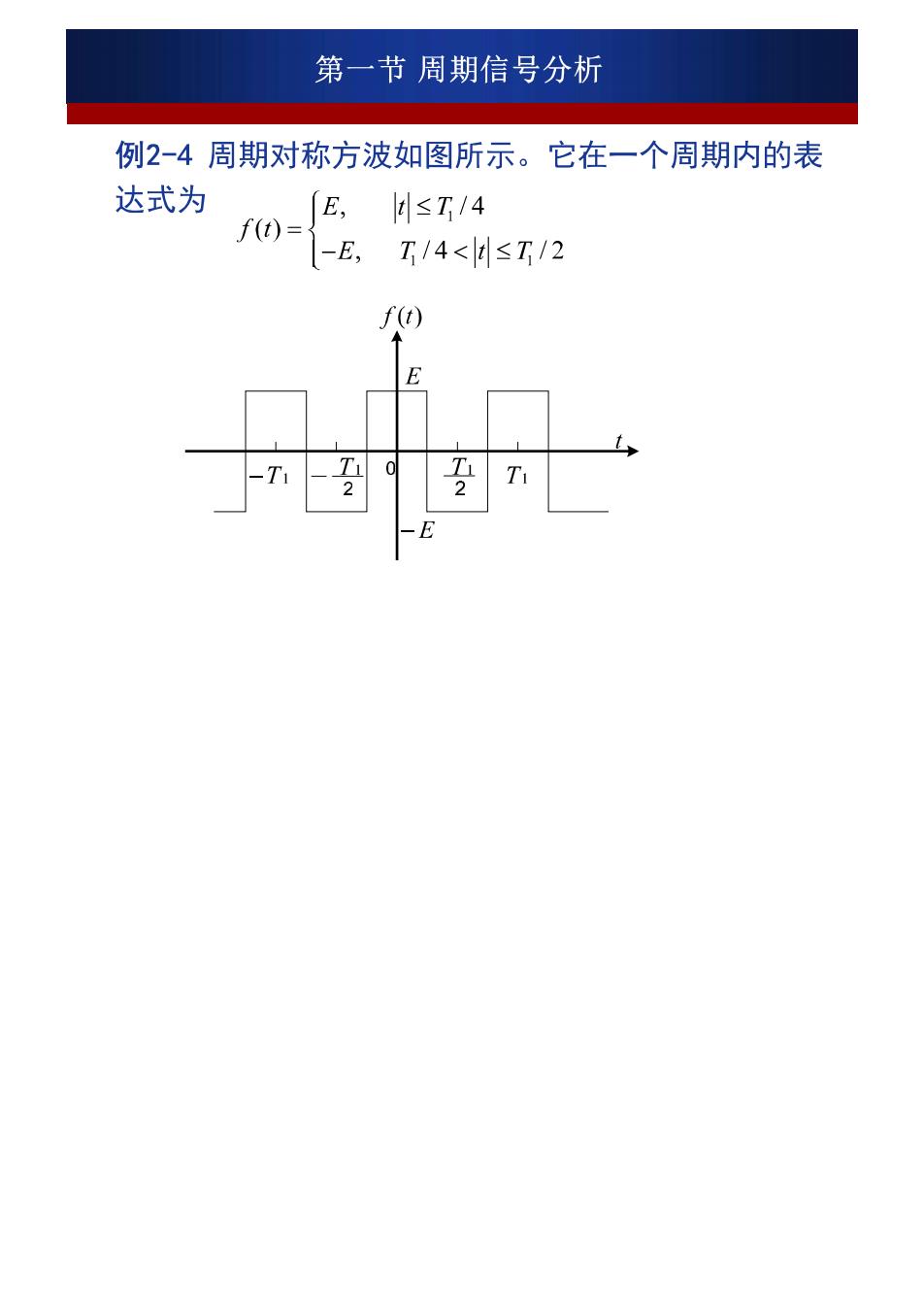
第一节周期信号分析 例2-4周期对称方波如图所示。它在一个周期内的表 达式为 E,4≤T/4 f(t)= -E,T14<4≤T/2 +=