
第三节二维渗流与流网当计算二维或三维渗流问题时,达西定律要用微分形式来表达。当闸坝很长且断面轮廓一致时,可按二维平面渗流问题处理1
1 第三节 二维渗流与流网 ◼ 当计算二维或三维渗流问题时,达西定 律要用微分形式来表达。 ◼ 当闸坝很长且断面轮廓一致时,可按二 维平面渗流问题处理

、平面渗流的基本方程稳定渗流是指当上下游水位差保持恒定时的渗流(图2一14)。稳定渗流场中的测管水头h以及流速等渗流要素仅是位置的函数而与时间无关。2
2 一、平面渗流的基本方程 ◼ 稳定渗流是指当上下游水位差保持恒定 时的渗流(图2-14)。稳定渗流场中的 测管水头h以及流速等渗流要素仅是位置 的函数而与时间无关
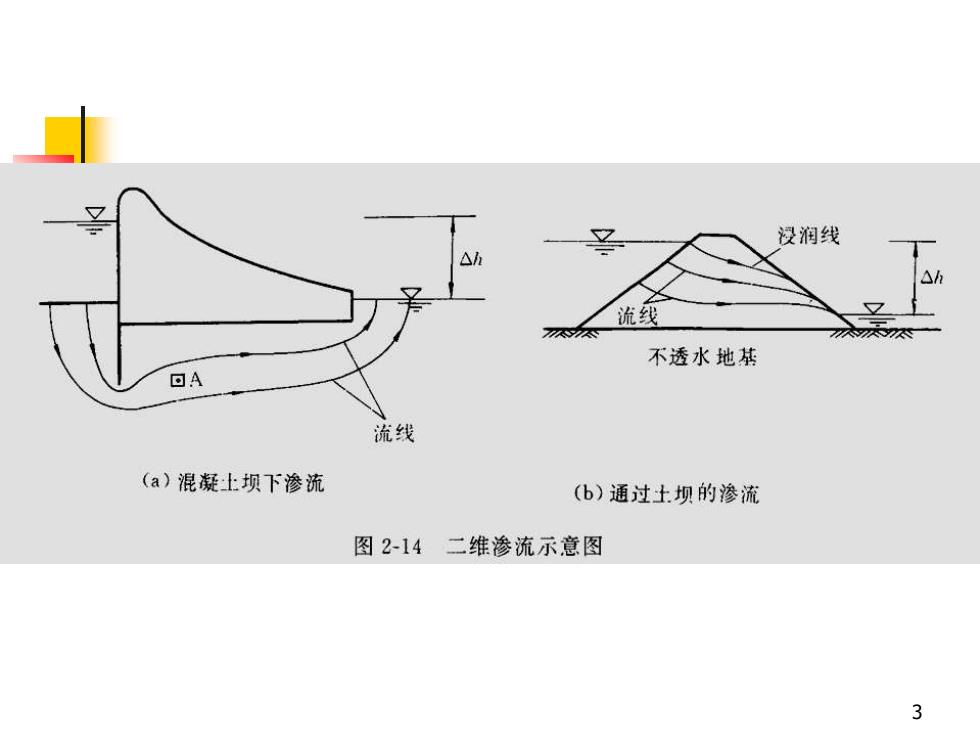
没润线Ah27流线1不透水地基DA流线(a)混凝上坝下渗流(b)通过土坝的渗流图2-14二维渗流示意图3
3
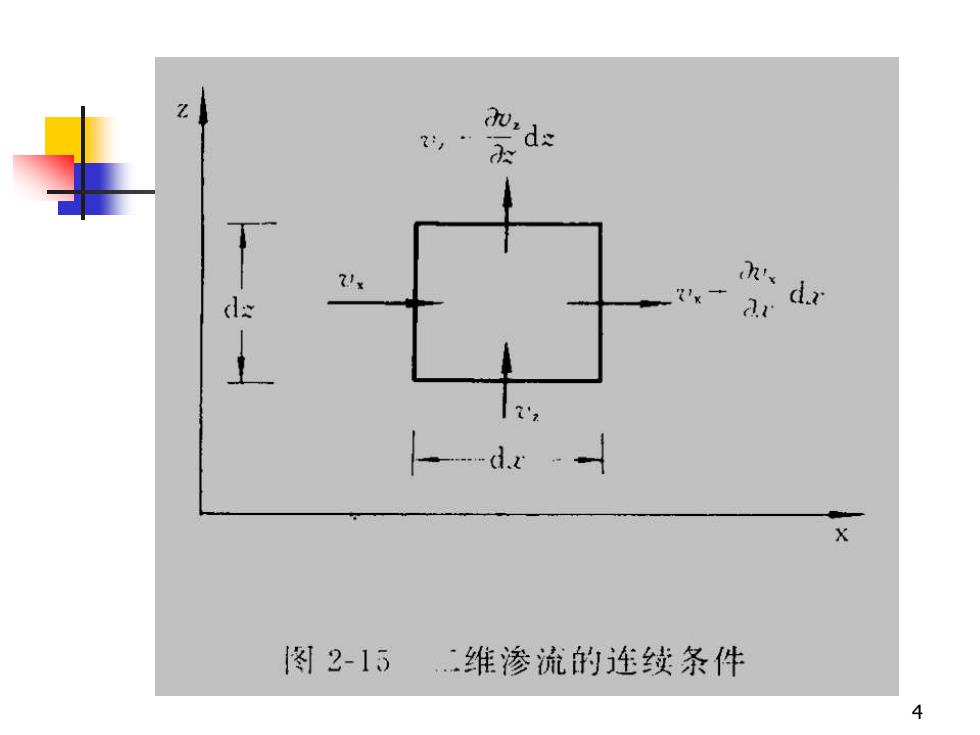
aro,AZxd.d11图]2-15二维渗流的连续条件
4

在稳定渗流场中A处取一微元土体,厚度设为dy=1,则dqe = Vx ×(dz×l)+Vz ×(dx×l)1×(dz×1)+×(dx×l)V-+dzdx5
5 ◼ 在稳定渗流场中A处取一微元土体,厚度 设为dy=1,则 dq = v (dz1) + v (dx1) e x z ( 1) ( 1) + + = + d z d x z v d x d z v x v d q v z z x o x

根据水流连续原理,单位时间内流入和流出微元体的水量应相等,即可得出Ovr + Ov.二=0(2 -28)axOz式(2一28)即为二维渗流连续方程。6
6 ◼ 根据水流连续原理,单位时间内流入和 流出微元体的水量应相等,即可得出 式(2-28)即为二维渗流连续方程。 = 0 (2 - 28) + z v x vx z

根据达西定律,对于各向异性土,(2 -29)=kV=k.i(2-30)kV, =k.i二式中,k、k一分别为x和z方向的渗透系数;h一测管水头。7
7 ◼ 根据达西定律,对于各向异性土, 式中,kx、kz—分别为x和z方向的渗透系数; h—测管水头。 (2 -30) (2 - 29) z h v k i k x h v k i k z z z z x x x x = = = =

将式(2一29)和(2一30)代入式(2一28)可得出:α?ha?h(2 -31):0axQz8
8 ◼ 将式(2-29)和(2-30)代入式(2- 28)可得出: 0 (2 -31) 2 2 2 2 = + z h k x h kx z

对于各向同性的均质土,k=k,则式(2一31)可表达为:a?h. a?h0(2 -32)ax?Qz29
9 ◼ 对于各向同性的均质土,kx=kz,则式(2 -31)可表达为: 0 (2 -32) 2 2 2 2 = + z h x h

■式(2一32)为平面稳定渗流的基本方程式即拉普拉斯方程。该方程描述了渗流场内部的测管水头h的分布。通过求解一定边界条件下的拉普拉斯方程,即可求得该条件下的渗流场。10
10 ◼ 式(2-32)为平面稳定渗流的基本方程 式即拉普拉斯方程。该方程描述了渗流 场内部的测管水头h的分布。通过求解一 定边界条件下的拉普拉斯方程,即可求 得该条件下的渗流场