
试卷代号:1024 座位 中央广播电视大学2009一2010学年度第二学期“开放本科”期末考试 信号处理原理 试题 2010年7月 题 号 二 三 四 五 六 总 分 分数 夜 分 评卷人 一、判断题(每小题3分,共15分) Sa(t)dt=π/3。 2.实信号的傅立叶变换的相位频谱是偶函数。 3.拉普拉斯变换满足线性性。 4.信号在频域中压缩等效于在时域中压缩。 5.单位阶跃序列的Z变换结果一定是常数。 得 分 评卷人 二、单项选择题(每小题5分,共25分) 1.使用计算机来处理信号,需涉及下列步骤( )。 A.编码,传输,解码 B.模数转换,数字信号处理,数模转换 C.平移,反褶,相乘 D.采样,量化,计算 2.卷积不具有的特性是()。 A.交换律 B.结合律 C.分配律 D.互补性 180
试卷代号 座位号 中央广播电视大学 2010 度第二学 开放 考试 信号处理原理试题 2010 年7 题号 /-A- 总分 分数 得分|评卷人 -、判断题(每小题 3分,共 5分) 1. ( ) 2. 3. 拉斯变 满足 性性 4. 号在频 缩等 5. 的Z 换结 常数 得分|评卷人 二、单项选择题{每小题 5分,共 5分) 1.使用计算机来处理信号,需涉及下列步骤( )。 A. 码B. 号处理 数模 C. 乘D. 2. 特性是 )。 A. 交换 B. 结合 C. 律D. 180
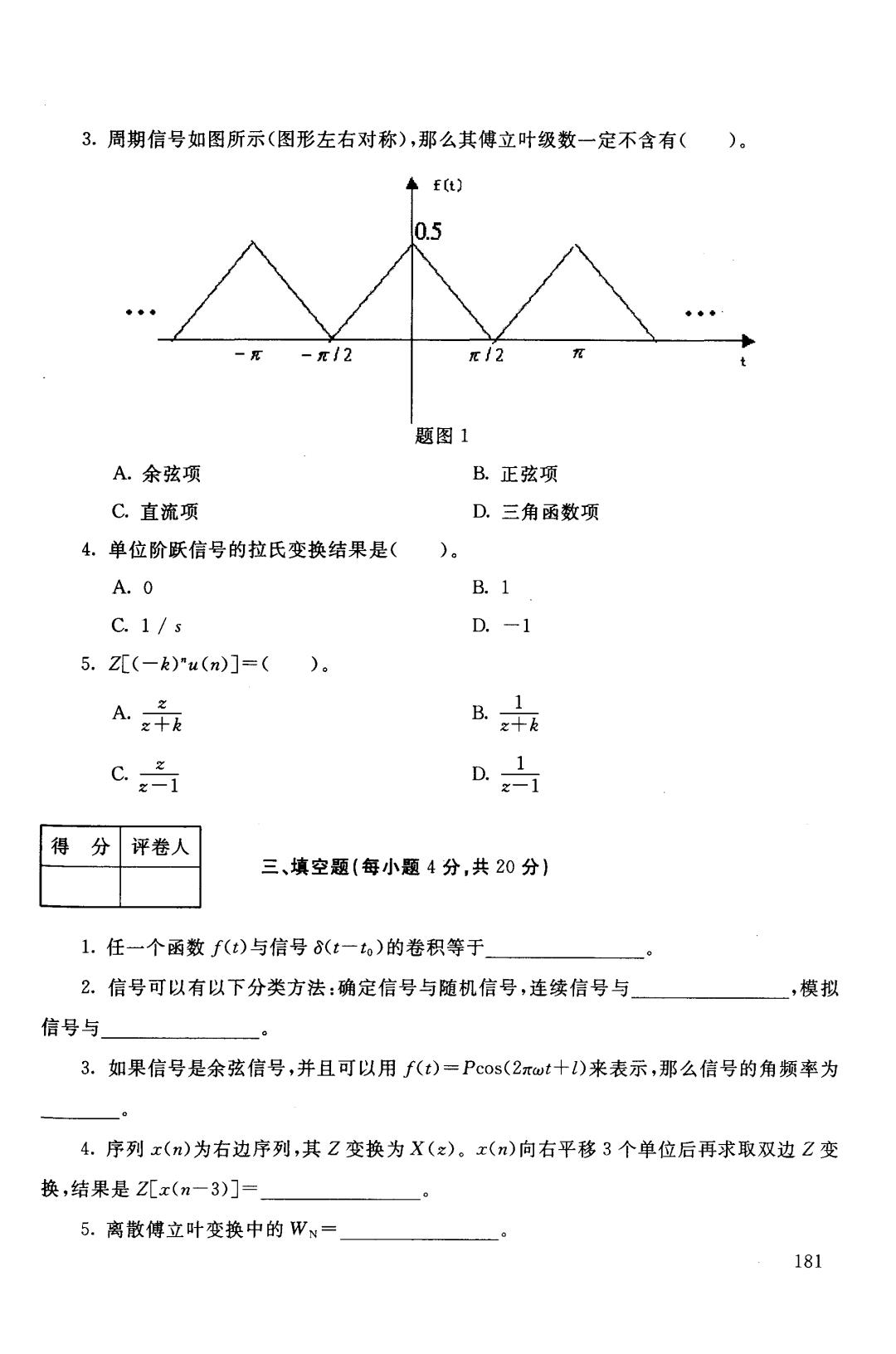
3.周期信号如图所示(图形左右对称),那么其傅立叶级数一定不含有()。 ◆ft 0.5 -π/2 π/2 题图1 A.余弦项 B.正弦项 C.直流项 D.三角函数项 4.单位阶跃信号的拉氏变换结果是( )。 A.0 B.1 C.1/s D.-1 5.Z(-k)"u(n)]=()。 A千 B+6 n 得分 评卷人 三、填空题(每小题4分,共20分) 1.任一个函数f(t)与信号6(t一to)的卷积等于 2。信号可以有以下分类方法:确定信号与随机信号,连续信号与 ,模拟 信号与 3.如果信号是余弦信号,并且可以用f(t)=Pcos(2πwt十l)来表示,那么信号的角频率为 4.序列x()为右边序列,其Z变换为X(之)。x(n)向右平移3个单位后再求取双边Z变 换,结果是Z兀x(n-3)]= 5.离散傅立叶变换中的W= 181
3. 所示 对称 ,那么其傅立叶级数一定不含有( )。 f(t) 0.5 • • • • • • -1f: Td2 17: t A. C. 直流 4. 换结果是 A. 0 C. 1 / s 5. Z[(-k)"u(n)J=( )。 题图 B.正弦项 D.三角函数项 B. 1 D. 一I z A. • l B. ~~ z C. z- 1 D. z- 得分|评卷人 三、填空题{每小题4分,共 0分) ,模拟 1.任一个函数 )与信号 to) 2. 号可 方法 定信 随机 信号与 3. t ) = Pcos(2πω 表示 4. 的 为右 其Z 移3 个单位后 取双边Z 换,结果是 5. 181
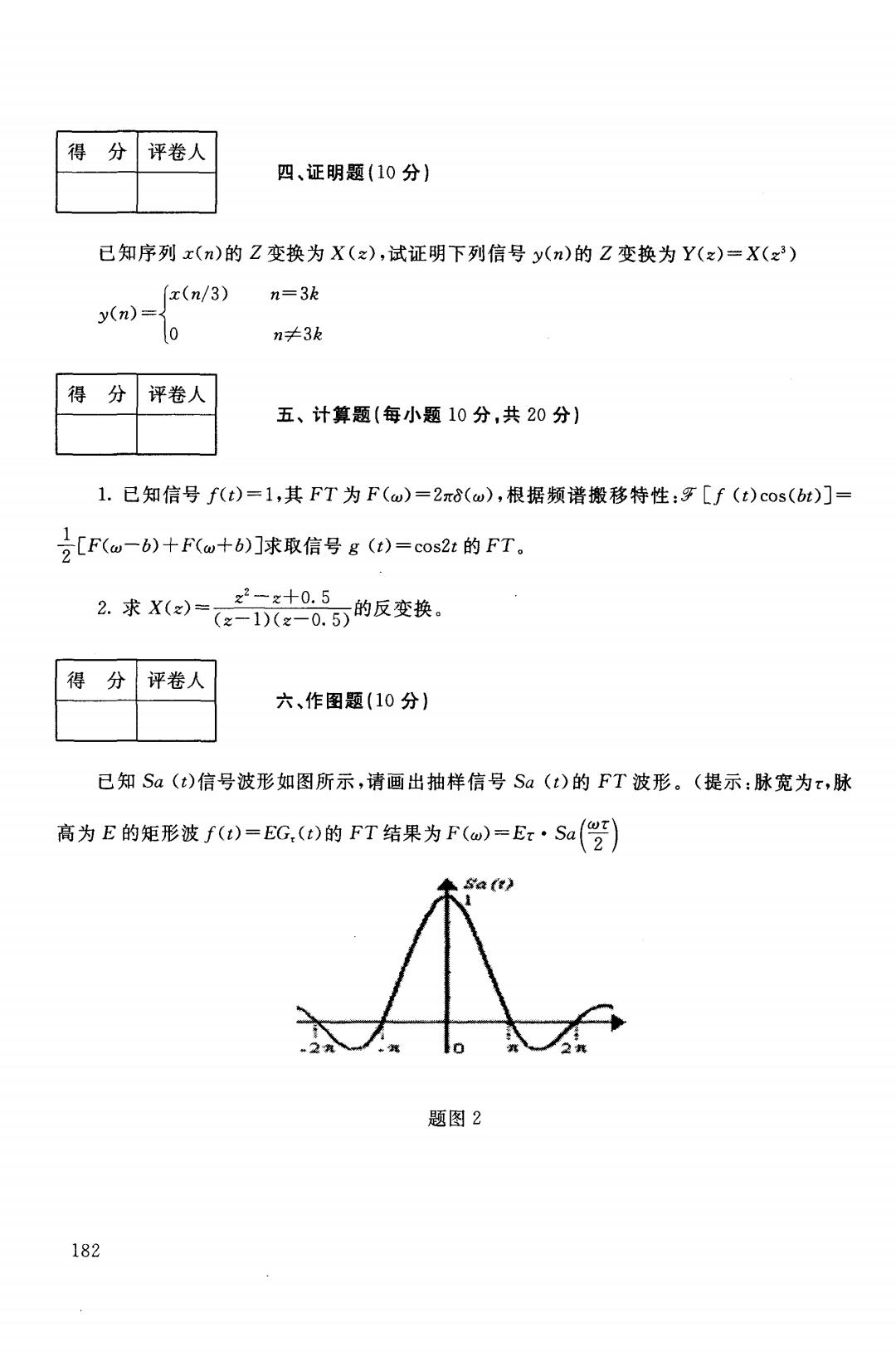
得分 评卷人 四、证明题(10分)】 已知序列x(n)的Z变换为X(z),试证明下列信号y(n)的Z变换为Y(z)=X(x3) x(n/3) n=3k y(n)= 0 n≠3k 得 分 评卷人 五、计算题(每小题10分,共20分) 1.已知信号f(t)=1,其FT为F(ω)=2πd(w),根据频谱搬移特性:牙[f(t)cos(bt)]= 号[F(u一6)+Fu+b)]求取信号g()=cos2:的FT。 2.求X()= 的反空换 得 分 评卷人 六、作图题(10分) 已知Sa(t)信号波形如图所示,请画出抽样信号Sa(t)的FT波形。(提示:脉宽为x,脉 高为E的矩形波f)=EG,()的FT结果为F(a)=Ex·Sa(?) a》 题图2 182
得分|评卷人 四、证明题 0分) 已知序列 C川的 Z变换为 C功,试证明下列信号 (川的 Z变换为 x(n/3) n=3k y(n)= o 笋3k 得分|评卷人 五、计算题(每小题 0分,共 0分} 1.已知信号 (t l, T为 ,根据频谱搬移特性:?7 [f (t)cos(bt)]= ÷〔 b) (t)= 的FT z2-z+ 0. 5 2. ="/唱、/ ~严、的反变换。 得分|评卷人 六、作圄题 已知 (t) 信号波 所示 (t)的 T波形。(提示:脉宽为 τ,脉 高为 E的矩形波 EG ω的 T结果为 Sa( $,然 I 题图 182

试卷代号:1024 中央广播电视大学2009一2010学年度第二学期“开放本科”期末考试 信号处理原理 试题答案及评分标准 (供参考) 2010年7月 一、判断题(每小题3分,共15分) 1.X 2.X 3.V 4.X 5.X 二、单项选择题(每小题5分,共25分) 1.B 2.D 3.B 4.C 5.A 三、填空题(每小题4分,共20分)》 1.f(t-to) 2.离散信号 数字信号 3.2rw 4.z-3X(x) 5.e 四、证明题(10分)》 证明: Y)=艺w() (4分) -芝a/3a= )x(m)(z)-m =:0 tn=o对 =X(z3) (6分) 五、计算题(每小题10分,共20分) 1.解:根据已知条件,f(t)=1,那么F(w)=2π8(w) (3分) 根据频谱搬移特性,3[f()cos(2)]-=[F(w一2)+F(u+2)] (4分) =×[2n80u-2)+2au+2)] =π6(w一2)+π6(w十2) (3分) 2.解:将X(之)分解为部分分式得 183
试卷代号 中央广播电视大学 2010 二学 开放 期 末考 信号处理原理试题答案及评分标准 (供参考) 2010 年7 一、判断题(每小题 1. X 2. X 3. v' 二、单项选择题{每小题 1. B 2. 0 3. B 三、填空题{每小题 2 0 4. X 5. X 4. C 5. A 1. f(t - to) 2. 散信 数字信号 3. 2πω 4. Z-3 X(z) 5.e 四、证明题(10分} 证明: +∞ y(z) = 2..: y(n)(z)-n (4 n= = 2..: x(n/3)(z)-n= 2..: x(m)(z)-3m n~ ∞m= =X(Z3) (6 五、计算题(每小题 2 0 1.解:根据已知条件 = ;r0' (3 根据频谱搬移特性 SF [f( t) 2 (4 0 , + " ? " 1-2d /w+-d++ (3 2. 分解 分式 183

得X0-1+-9”0可1+A+当 0.5z (4分) 可求出: A1=-1 A2=1 X)-1+22-05 (3分) 因此 x(n)=6(n)+u(n)-(0.5)"u(n) (3分) 六、作图题(10分) 答案:当x=2,E=0.5时,f(t)=EG,(t)=0.5G2(t),F(w)=Sa(w);f(-w)= 0.5G2(-w);F(t)=Sa(t) 由对偶性(g[F(t)]=2πf(一w)] F[F(t)]=9 [Sa(t)]=2xf(-w)=xGz(-w)=nG2(w) ◆武o) 01 答图1Sa(t)的FT 184
o. 5z / ,、/ -户、 1十一一←τ .. ~(;-: 可求出: A j=-l A2=1 X(z)=l+ 因此 x(n) =8(n) 以n) u(n) (4 (3 (3 六、作固题 答案:当 2 , E = 0.5 f (t) = EG, (t) = o. 5G2 (t) , F (ω) = Sa (ω); f (一 O. 5G2 (一 ;F(t) =Sa(t) 由对偶性 ff [F(t) J=2π 一ω)J ff [F(t)J=ff [Sa(t)J=2 (ω) Ftm) 184 -1 - 答图 Sa(t) 的FT