
试卷代号:1012 座位号 中央广播电视大学2009一2010学年度第二学期“开放本科”期末考试(半开卷) 计算机数学基础(2) 试题 2010年7月 题号 二 三 总 分 分数 得分 评卷人 一、单项选择题(每小题4分,共20分) 1.若近似值x的绝对误差限为ε=0.5×10-2,那么以下有4位有效数字的x值是(). A.0.9344 B.9.344 C.93.44 D.934.4 2.当线性方程组AX=b的系数矩阵A是()时,用列主元消去法解AX=b,A的主 对角线的元素一定是主元. A.上三角形矩阵 B.主对角线元素不为0的矩阵 C.正定对称矩阵 D.对称且严格对角占优矩阵 3.用p(x)拟合数据(x1,y1),(x2,y2),…,(xm,yn)的最小二乘法是选择p(x)使 ()最小 A2-, 79
试卷代号 座位号 中央广播电视大学 2010 学年 第二 放本 期末 计算机数学基础 2010 年7 题号 • 总分 分数 得分|评卷人 -、单项选择题(每小题 4分,共 0分) 1.若近似值 Z的绝对误差限为 XlO- 2,那么以下有 4位有效数字的 z值是( ). A.0.9344 B.9.344 C.93.44 D. 934. 4 2. 方程组 AX 的 系 数矩 阵A )时,用列主元消去法解 A的主 对角线的元素一定是主元. A. C. 正定对 B. 为O D. 格对 3. cp 拟 合 l ' Yl)' (工 ,只) ,… , ( Xn , Yn) 最 小 二 乘 择cp(X) ( )最小. A. 2:: (Yk ψ(Xk) )2 c. 2:: (Yk 一cp(Xk) ) B. IYk ψ(Xk) I D. (2:: (Yk 一cp(Xk» )2 79

4.已知m-4时牛顿一科关求积公式的科装系数C”一品,C0=碧C”=号那么 C4)=(). A. 16 0 c D. 7 5.用牛顿法求方程f(x)=0的近似根,选择初始值x应满足(). A.f(zo)f(zo)0 C.f"(xo)f()0 得分 评卷人 二、填空题(每小题4分,共20分) 6.用四舍五入的方法得到近似值x=0.0514,那么x的绝对误差限为 「10.750.751 7.设线性方程组AX=b的系数矩阵为A= 0.75 10.75 那么雅可比迭代矩阵 0.750.75 1 B。= 8.、已知数据(1,3.8),(2,7.2),(3,10),用拟合曲线拟合这些点,计算得法方程组为 9.已知函数值f(0.7)=0.343,f(1.1)=1.331,f(1.5)=3.375,用抛物线求积公式 计算定积分fx)d,那么fx)z≈ 10.设函数f(x)在区间[0,1]上连续,若满足 ,则方程f(x)=0 在区间[0,1]一定有实根. 80
4. = 科茨求积公 科茨 90 '~1 - 45 , v Z - 15 ' C~4) = ( ). A. 90 B c.主15 D. 2. 90 5. 法求方程 近似根 满足 ). A. J'(xo) f(xo) 0 C·f'(xo)f(xo)<O D. f'(xo)f(xo»o 得分|评卷人 二、填空题{每小题 6. 舍五 方法得 对误 限为 • 1 o. 75 o. 75 7. 方程 的 系 为A = 10. 75 1 o. 751 雅可 O. 75 o. 75 1 Bo = • 8. C1 3. ,(2 ,7.2) ,(3 这些 算得法方 • 9. 7) = 0. 343 , f( 1. 1) = 1. 331, f( 1. 5)=3. 375 抛物 fJ Z EGZ ~~ ptB , , , , , " VHV zd z fJ 目, 10. 间[0 1J 在区间 一定 80 ,则方程

得 分 评卷人 三、计算题(每小题15分,共60分) 11.用雅可比迭代法解线性方程组 10x1-2x2-x3=3 -2x1+10x2-x3=15 -x1-2x2+5x3=10 从初始值Xo)=(0,0,0)T开始,计算出第3次迭代结果,并要求写出迭代公式,计算过程 中保留4位小数。 12.已知函数值f(0)=6,f(1)=10,f(3)=46,f(4)=82,f(6)=212,求函数的四阶均差 f(0,1,3,4,6)和二阶均差f(4,1,3). 13.将区间[1,9]作8等分,试用复化梯形公式求积分 V6-5d 的近似值.保留4位小数、 14.用弦截法求方程x5十3x一1=0在[0.3,0.4]之间的一个近似根,满足 |x1一x≤0.01.保留4位小数. 81
得分|评卷人 三、计算题{每小题 5分.共 0分) 1. 用雅 迭代法解 程组 10xI -Xa =3 2一句 -Xl +5 从初始值 O, O, O T开始,计算出第3次迭代结果,并要求写出迭代公式,计算过程 中保留 4位小数. 12. 值/(0)=6 d (l) = 10 , / ( 3) =46 , / ( 4) =82 , / ( 6) =212 /(0 ,1 ,3 ,4 的 和 阶均差/(4 ,1 ,3). 13. 区 间 9J 作8 公式 J: J6x-5dx 的近似值.保留4位小数. 14. 法 求 程X + 3x - 1 = 在[0.3 0.4] 间 的 IXH-I -X. Iζ0.01 .保留 4位小数. 81

试卷代号:1012 中央广播电视大学2009一2010学年度第二学期“开放本科”期末考试(半开卷) 计算机数学基础(2)试题答案及评分标准 (供参考) 2010年7月 一、单项选择题(每小题4分,共20分) 1.C 2.D 3.A 4.B 5.D 二、填空题(每小题4分,共20分) 6.0.00005 「0 -0.75-0.75 7. -0.75 0 -0.75 -0.75-0.75 0 3a。+6a1=21 8. 6a0+14a1=48.2 9.1.206 10.f(0)f(1)<0 三、计算题(每小题15分,共60分)】 11.解:迭代公式为. (x+1)=0.2x十0.1x+0.3 x8+D=0.2x®+0.1x+1.5(k=0,1,2) (4分) x+D=0.2x)+0.4x+2 当k=0时,X=(0,0,0)T,易得X1)=(0.3000,1.5000,2.0000)T. 当k=1时,X1)=(0.3000,1.5000,2.0000)T. (7分) x2=0.2X1.5+0.1×2+0.3=0.8000 x2=0.2×0.3+0.1×2+1.5=1.7600 x2=0.2×0.3+0.4×1.5+2=2.6600 82
试卷代号 中央广播电视大学 0 0 2010 度第 期末考试 计算机数学基础 试题 及评 (供参考) 2010 年7 8. -、单项选择题{每小题 1. C 2. 0 3. A 二、填空题(每小题 6. 0.00005 o - 0.75 75 7. 7 5 75 75 - o. 75 0 切。十 =21 归。十 =48.2 9. 1. 206 10. j(O)j(1)<O 三、计算题(每小题 1. 迭代公式 4. B 5. 0 xik+l) = O. 2X~k) 1x~k) + O. 3 zj = O. 2xi Ix 1. 5 (k=0 ,1 ,2) (4 工;肿 o. 2xi o. 4x~的 = (0 ,0 ,0 得X( I)=(0.3000 1. 5000, 2.0000)T. 当是 0 0 0 1. 5000 , 2.0000)T. (7 xi 2 ) =0.2 XL 十0.1 X 十0.3 =0.8000 X~2) = O. 2 X o. 十0.1 X 1. 5 = 1. 7600 X~2) = O. 2 X o. 十0.4 X 1. 十2 =2.6600 82
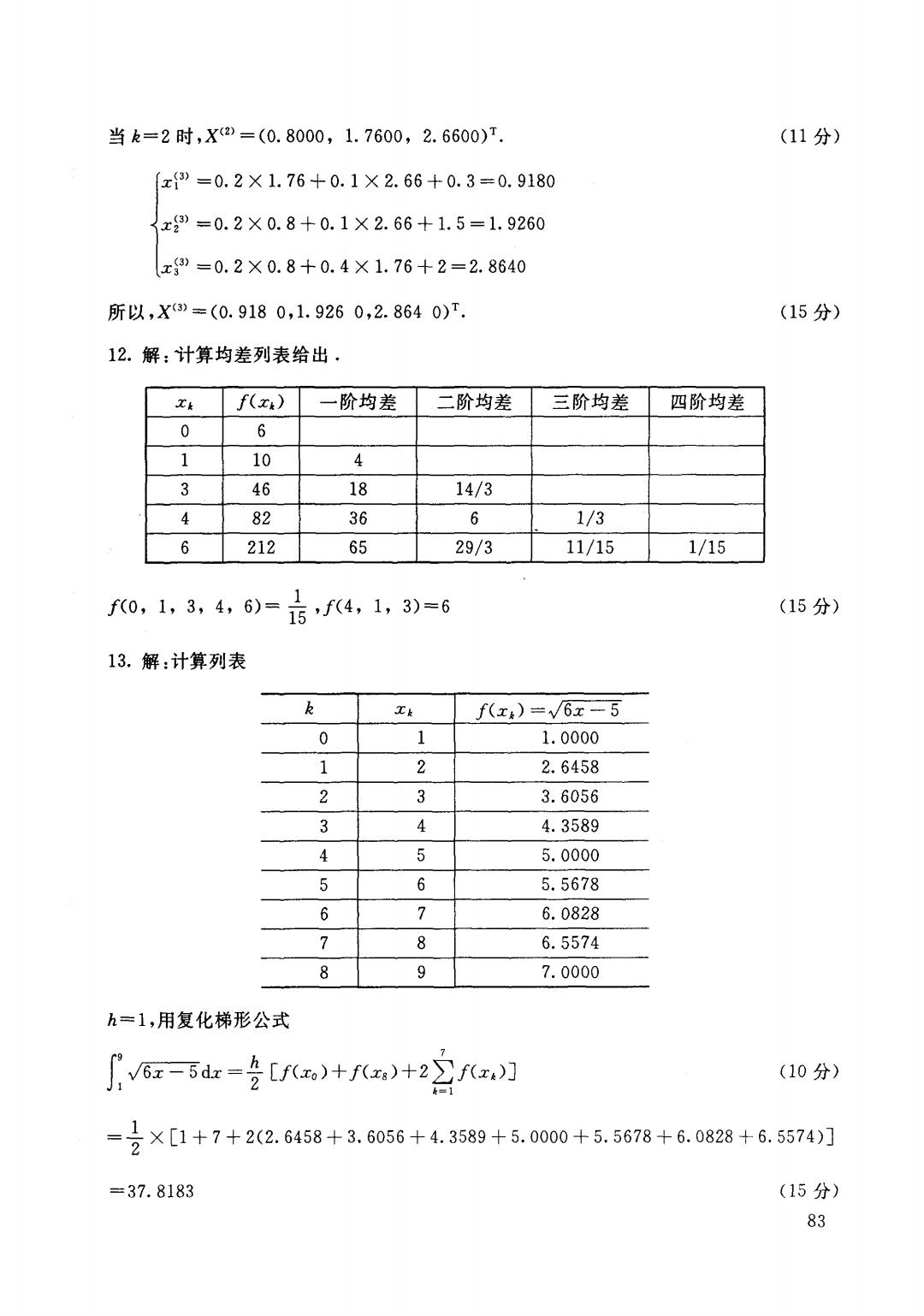
当k=2时,X2)=(0.8000,1.7600,2.6600)T. (11分) x{3)=0.2×1.76+0.1×2.66+0.3=0.9180 x3)=0.2×0.8+0.1×2.66+1.5=1.9260 x3)=0.2×0.8+0.4×1.76+2=2.8640 所以,X3)=(0.9180,1.9260,2.8640)T (15分) 12.解:计算均差列表给出, Ck f(x.) 一阶均差 二阶均差 三阶均差 四阶均差 0 6 1 10 3 46 18 14/3 4 82 36 6 1/3 6 212 65 29/3 11/15 1/15 f(0,1,3,4,6)= f(4,1,3)=6 1 (15分) 13.解:计算列表 k 工k f(xB)=√6x-5 0 1 1.0000 1 2.6458 2 3 3.6056 3 4 4.3589 4 6 5.0000 5 6 5.5678 6 1 6.0828 7 8 6.5574 8 9 7.0000 h=1,用复化梯形公式 月a百d=会[,)+f)+22f✉刀 (10分) =合×[1+7+22.6458+3.6056+4.3589+5.000+5.5678+6.0828+6.574] =37.8183 (15分) 83
8 0 0 1. 6 6 0 0 xi 3 ) =0.2 X l. 76 + 0.1 X 2. 66 十0.3 =0.9180 X~3) = O. 2 X O. 8 + O. 1 X 2. 66 1. 5 = 1. 9260 xj3) = O. 2 X O. 十0.4 X l. 76 + 2 =2.8640 所以, 0 , 1. 926 0 ,2.864 O)T. 12. Xi f(Xi) 一阶均差 二阶均差 三阶均差 四阶均差 O 6 1 10 4 3 46 18 14/3 4 82 36 6 1/3 6 212 65 29/3 11/15 1/15 f(0 ,I, 3, 4, 6) = i,f (4, 1, 3) = 6 15 13. h Xi f( =';6x - 5 O 1 1. 0000 l 2 2. 6458 2 3 3.6056 3 4 4. 3589 4 5 5.0000 5 6 5.5678 6 7 6.0828 7 8 6.5574 8 9 7. 0000 h=l 用 复 梯形公式 J:而可 (1 (1 (1 (1 =÷× 4.3589 十5.0000 + 十6.0828 十6 =37.8183 (1 83

14.解:设f(x)=x5十3x一1,取x=0.3,x1=0.4,f(0.3)0, 故f(x)=0在[0.3,0.4]内有根. (3分) 建立迭代公式 Entl =In- 总+3,-1,(x,-xr1)(n=1,2…) (6分) x员十3xm-x;1-3xm-1 当n=1时, x2=0.4 0.45十3×0.4-1 0.4+3×0.4=0.3°-3×0.3(0.4-0.3)=0.3317, x2-x1=0.0683. (10分) 当n=2时, 0.33175+3×0.3317-1 x=0.3317-0.33179+3X0.3317-0.40-3X0.40.3317-0.4)=0.3320, {x3-x2=0.0003. (13分) 取x¥≈0.3320为原方程的近似根. (15分) 84
14. 5+3x-1 取xo=O. 3 ,xI =0.4 :> O O在 建立迭代公式 一(x x~ +3 -xn-l)(n=1 ,2,. . . ) z; 十3zn-zLI-3zr1" 0.4 十3 X O. 4-1 xz=0.4- ,.. ~t; ,向、~..... .......r:;. ....、,~ =0.3317 , |叫一句 (3 (6 (1 O. 33175 +3 X O. 3317 - 1 X3 =0.3317 -;:….....~ -…… A aRLJ 3 3 3 2 84 IX3 - Xz 1=0. 0003. 3320 方程 (1 (1