
线性代数 山东理工大学
线性代数 山东理工大学

第4章线性方程组 §4.2齐次线性方程组
§4.2 齐次线性方程组 第4章 线性方程组

设齐次线性方程组为 41X1+ 012X2+L = 0 L21X1 +022X2 +L十 A2nXn 0 (1) M M M MMM M MM m22+L+AmXn =0 1 012 21 2 L 则称矩阵A= d2n 为方程组1)的系数矩阵。 M MM M L
设齐次线性方程组为 则称矩阵 11 12 1 21 22 2 1 2 n n m m mn a a a a a a A a a a = L L M M M M L 为方程组(1)的系数矩阵。 11 1 12 2 1 21 1 22 2 2 1 1 2 2 0 0 (1) 0 n n n n m m mn n a x a x a x a x a x a x a x a x a x + + + = + + + = + + + = L L M M M M M M M M M L
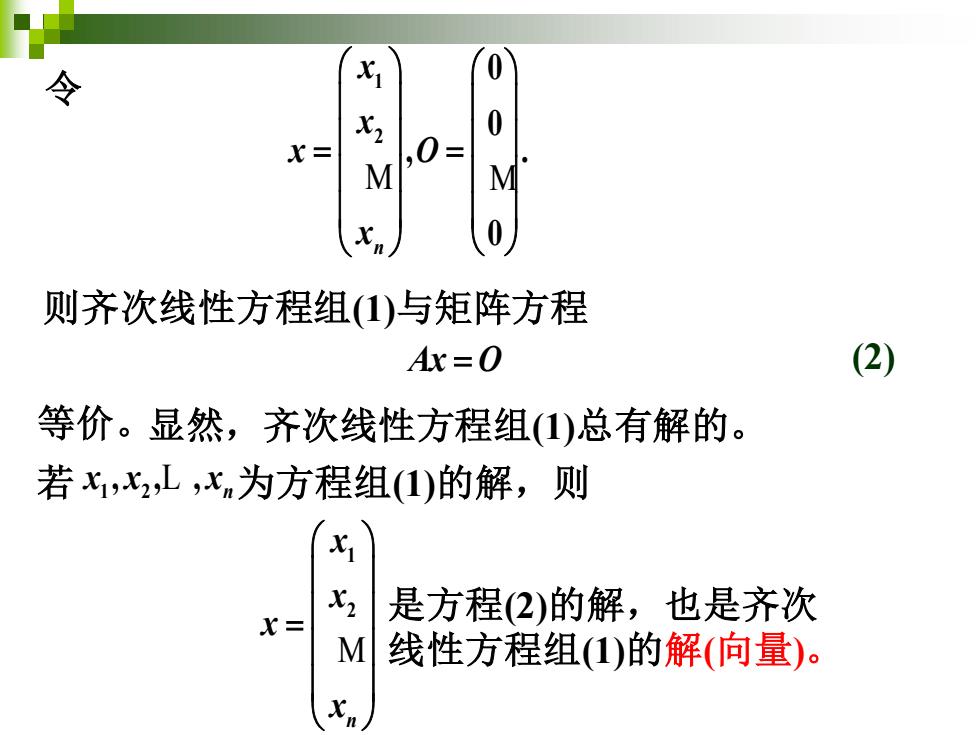
1 0 0 X= ,0= M 则齐次线性方程组()与矩阵方程 Ax=0 (2) 等价。显然,齐次线性方程组(1)总有解的。 若x,心2L,xn为方程组(1)的解,则 七 X2 是方程(2)的解,也是齐次 x= M 线性方程组(1)的解(向量)
令 1 2 0 0 , . 0 n x x x O x = = M M 则齐次线性方程组(1)与矩阵方程 显然,齐次线性方程组(1)总有解的。 Ax O= (2) 若 x x x 1 2 , , , L n 为方程组(1)的解,则 是方程(2)的解,也是齐次 线性方程组(1)的解(向量)。 1 2 n x x x x = M 等价
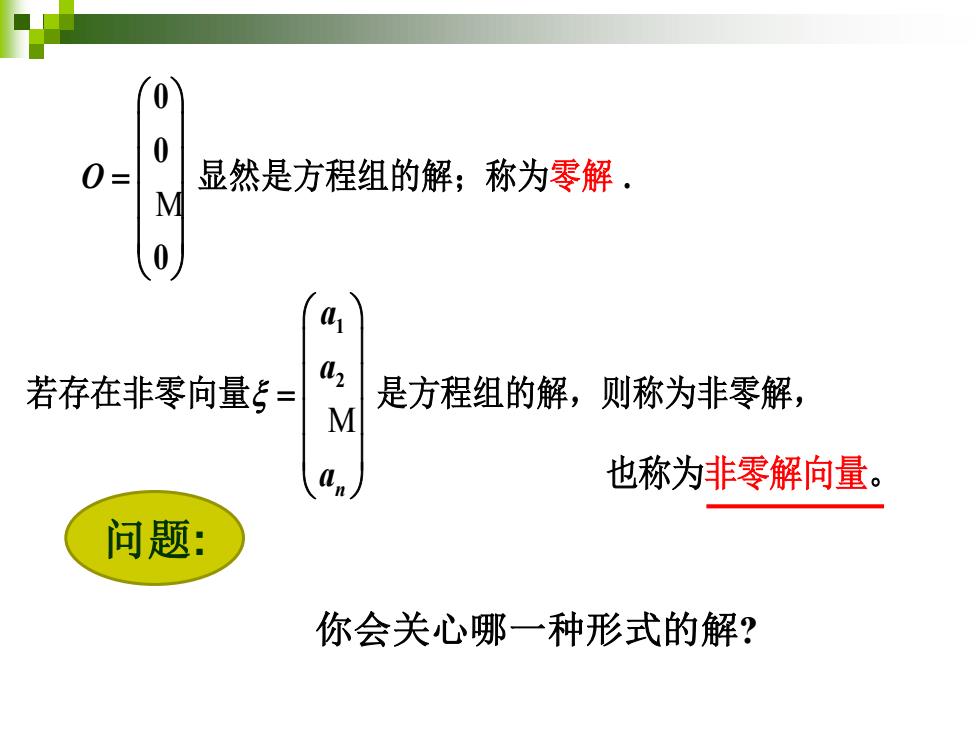
0 0 显然是方程组的解;称为零解. M 0 若存在非零向量5= 02 是方程组的解,则称为非零解, M 也称为非零解向量。 问题: 你会关心哪一种形式的解?
0 0 . 0 O = M 显然是方程组的解;称为零解 1 2 n a a a = M 若存在非零向量 是方程组的解,则称为非零解, 也称为非零解向量。 问题: 你会关心哪一种形式的解?

1.齐次线性方程组(1)有解的条件:总是有解 想一想 齐次线性方程组:R(A)=R(A) 定理1:齐次线性方程组Ax=O有非零解台R(A)<m 定理2:齐次线性方程组Ax=O只有零解台(A)=n 推论:齐次线性方程组Axm七x1=Ox1只有零解, 台R(A)=n即A≠0,即系数矩阵A可逆
1. 齐次线性方程组(1)有解的条件 定理1:齐次线性方程组 Ax O= 有非零解 R A n ( ) 定理2:齐次线性方程组 Ax O= 只有零解 = R A n ( ) 想一想 齐次线性方程组: R A( ) = R A( ) 推论:齐次线性方程组 A x O n n n n 1 1 = 只有零解, = R A n ( ) 即 A 0, 即系数矩阵A可逆。 :总是有解

解向量对加法封闭 2.齐次线性方程组(1)解的性质 性质1: 若51,52是()的解向量, 则x=5+52仍然是(1)的解向量。 设51,52是Ax=O的两个解向量,则 A51=0,A52=0. ∴.A(51+52)=A51+A52=0+0=O
2. 齐次线性方程组(1)解的性质 性质1:若 1 2 , 是(1)的解向量, 则 x = + 1 2 仍然是(1)的解向量。 设 1 2 , 是 Ax O= 的两个解向量,则 1 A O = , 2 A O = . 1 2 + A( ) A A 1 2 = + = + O O = O. 解向量对加法封闭

解向量对数乘封闭 性质2 若5是)的解向量, 则x=k5,k为常数,是()的解向量。 设5是Ax=O的解向量,则 A5=O. .A(k5)=k(A5)=kO=O. 解空间:AK=O的所有解向量的集合,对加法和数乘 都封闭,所以构成一个向量空间,称为这个 齐次线性方程组的解空间
解空间: Ax O= 的所有解向量的集合,对加法和数乘 都封闭,所以构成一个向量空间,称为这个 齐次线性方程组的解空间。 性质2:若 是(1)的解向量, 则 x k k = , 为常数,是(1)的解向量。 设 是 Ax O= 的解向量,则 A O = . A k( ) = k A( ) = kO = O. 解向量对数乘封闭

如何确定一 个向量空间V? 最大无关组 设向量组41,42,L,0m是V的一组基,则 V=xx=k a+hgazt+kmam k,kz,kmER
如何确定一 个向量空间V? 设向量组 a a a 1 2 , , , L m 是V的一组基,则 V x x k a k a k a k k k R = = + + + | , , , 1 1 2 2 1 2 m m m 最大无关组

3.基础解系 设51,52,L,5m,是Ax=0的解,满足 (1)5,52,L,5m-,线性无关; (2)Ax=0的任一解都可以由5,52,L,5m,线性表示。 则称51,52,L,5m,是A=0的一个基础解系。 定理: 设A是m×n矩阵,如果R(A)=r<n, 则齐次线性方程组Ax=O的基础解系存在, 且每个基础解系中含有n一r个解向量
3. 基础解系 设 1 2 , , , n r L − 是 Ax O= 的解,满足 1 2 1 , , , n r ( ) L − 线性无关; (2 )Ax O= 的任一解都可以由 1 2 , , , n r L − 线性表示。 则称 1 2 , , , n r L − 是 Ax O= 的一个基础解系。 定理:设 A 是 m n 矩阵,如果 R A r n ( ) , = 则齐次线性方程组 Ax O= 的基础解系存在, 且每个基础解系中含有 n r − 个解向量