
JIAOTONG UNIVERSITY 1096 Systems Engineering Lecture 7-2 Multi-Objective Optimization Instructor(s) Prof.Jianjun Gao Department of Automation School of Electronic Information and Electrical Engineering 2014 Spring
Systems Engineering Instructor(s) + - 2014 Spring Multi-Objective Optimization Prof. Jianjun Gao Department of Automation School of Electronic Information and Electrical Engineering Lecture 7-2
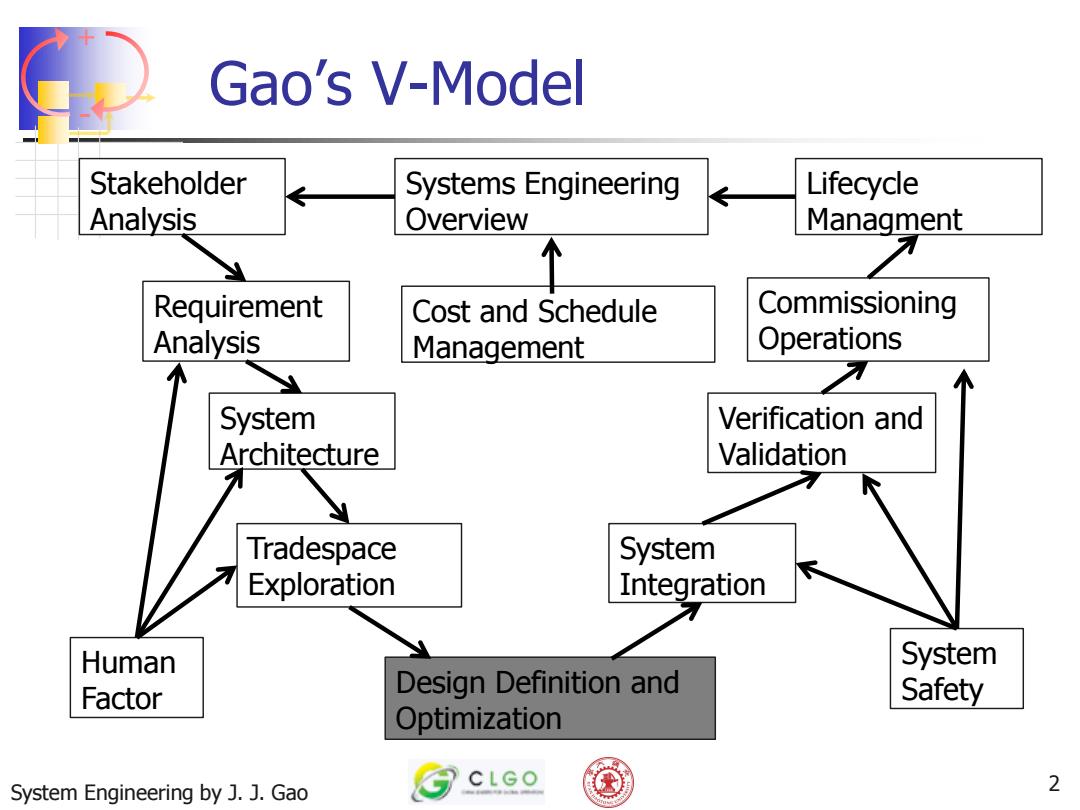
Gao's V-Model Stakeholder Systems Engineering Lifecycle Analysis Overview Managment Requirement Cost and Schedule Commissioning Analysis Management Operations System Verification and Architecture Validation Tradespace System Exploration Integration Human System Factor Design Definition and Safety Optimization CLGO System Engineering by J.J.Gao 2
+ - System Engineering by J. J. Gao 2 Gao’s V-Model Stakeholder Analysis Requirement Analysis System Architecture Tradespace Exploration Design Definition and Optimization System Integration Verification and Validation Commissioning Operations Lifecycle Managment Systems Engineering Overview Cost and Schedule Management Human Factor System Safety

Today's Agenda Convex Optimization(Single Variable) Mini-Tutorial on Convex function ■MOO Formulation MOO:The weighting Method MOO:E-Constraint Method MOO:Goal Programming CLGO System Engineering by J.J.Gao 3
+ - 3 Today’s Agenda System Engineering by J. J. Gao Convex Optimization(Single Variable) Mini-Tutorial on Convex function MOO Formulation MOO: The weighting Method MOO:𝜖-Constraint Method MOO: Goal Programming

Today's Agenda Convex Optimization(Single Objecitve Function) Optimization Problem Classification Multi-objective optimization Goal Programming CLGO System Engineering by J.J.Gao 4
+ - 4 Today’s Agenda System Engineering by J. J. Gao Convex Optimization(Single Objecitve Function) Optimization Problem Classification Multi-objective optimization Goal Programming

Mathematical Optimization (mathematical)optimization problem minimize fo(x) subject to fi(x)<bi,i=1,...,m =(1,...,n):optimization variables ●fo:Rm一R:objective function ●fi:Rn一R,i=1,..,m:constraint functions optimal solution has smallest value of fo among all vectors that satisfy the constraints System Engineering by J.J.Gao CLGO 5
+ - System Engineering by J. J. Gao 5 Mathematical Optimization

Scope of Optimization o Optimal design manufacturing o Inverse Problems:output known,find input. oParameter optimization for optimal performance o System modeling o Planning oOptimal control o Forecasting and prediction o Data mining(classification,clustering,pattern recognition) o Machine learning o Bioinformatics CLGO System Engineering by J.J.Gao 6
+ - System Engineering by J. J. Gao 6 Scope of Optimization

Solving Optimization Problem General Optimization Problem Very difficult to solve Methods involve some compromise,e.g.,very long computational time,or not always finding the solution ■ Exceptions:Certain problem classes Least-Squares problem Linear programming problem Convex Optimizitioin problem CLGO System Engineering by J.J.Gao 7
+ - General Optimization Problem Very difficult to solve Methods involve some compromise, e.g., very long computational time, or not always finding the solution Exceptions: Certain problem classes Least-Squares problem Linear programming problem Convex Optimizitioin problem System Engineering by J. J. Gao 7 Solving Optimization Problem

Least Squares minimize 6()=‖Ax-bl3=∑1(ax-b)2. Here ARx (with k>n),af are the rows of A,and the vector 2 R"is the optimization variable. analytical solution:*=(ATA)-1ATb The basis of regression analysis,optimal design,many parameter estimation and data fitting methods. Reliable and efficient algorithms and software Computational time proportional to n2:(A E R*x") System Engineering by J.J.Gao CLGO 8
+ - System Engineering by J. J. Gao 8 Least Squares • The basis of regression analysis, optimal design, many parameter estimation and data fitting methods. • Reliable and efficient algorithms and software • Computational time proportional to

Linear Programming minimize cTa subject to afa s bi,i=1,...,m. Here the vectors c,a1,...,am E R"and scalars b1,...,bm E R are problem pa- rameters that specify the objective and constraint functions. It Has many applications.... no analytical formula for solution reliable and efficient algorithms and software computation time proportional to n2m if m =n;less with structure ●a mature technology CLGO System Engineering by J.J.Gao 9
+ - System Engineering by J. J. Gao 9 Linear Programming It Has many applications…

Convex Optimization solving convex optimization problems no analytical solution reliable and efficient algorithms computation time (roughly)proportional to max{n3,n2m,F},where F is cost of evaluating fi's and their first and second derivatives ●almost a technology using convex optimization often difficult to recognize many tricks for transforming problems into convex form surprisingly many problems can be solved via convex optimization CLGO System Engineering by J.J.Gao 10
+ - System Engineering by J. J. Gao 10 Convex Optimization