
第二章 物质的状态 m2.1气体 ■2.2液体 ■2.3固体
第二章 物质的状态 ◼ 2.3 固体 ◼ 2.2 液体 ◼ 2.1 气体

2.1 气体 ■理想气体 ■气体分子运动 ■实际气体 无机化学
无机化学 2.1 气体 ◼ 理想气体 ◼ 气体分子运动 ◼ 实际气体

2.1.1理想气体 分子不占体积,可看成几何质点,分子 间无吸引力,分子与器壁之间发生的碰 撞不造成动能的损失 无机化学
无机化学 2.1.1 理想气体 分子不占体积,可看成几何质点,分子 间无吸引力,分子与器壁之间发生的碰 撞不造成动能的损失
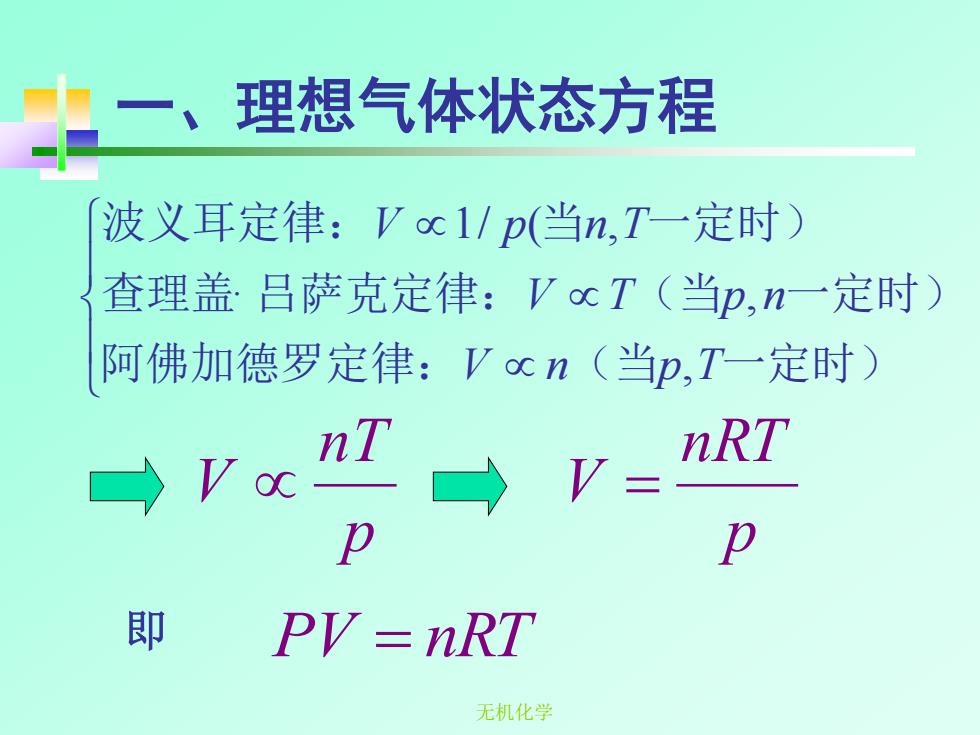
理想气体状态方程 波义耳定律:Voc1/p(当n,T一定时) 查理盖吕萨克定律:VocT(当p,n一定时) 阿佛加德罗定律:Vocn(当p,T一定时) nT nRT p p 即 PV=nRT 无机化学
无机化学 一、理想气体状态方程 即 阿佛加德罗定律: (当 一定时) 查理盖 吕萨克定律: (当 一定时) 波义耳定律: 当 一定时) V n p T V T p n V p n T , · , 1/ ( , p nT V p nRT V = PV = nRT

混合气体分压定律 当T一定时,在V体积内,设混合气体有种, 若各组分气体均为理想气体,则 P点V=n总RT=(n1+n2+.+n)RT n RT+n2 RT+.n;RT PiV+P2V+.+PV =(P1+p2+.+P)V P总=pi=P1+P2+.+P 无机化学
无机化学 二、混合气体分压定律 当T一定时,在V体积内,设混合气体有i种, 若各组分气体均为理想气体,则 P总V=n总RT=(n1+n2+.+ni )RT = n1 RT+ n2 RT+.niRT = P1V+P2V+.+PiV =(P1+p2+.+Pi )V P总= Σpi=P1+p2+.+Pi

由于PV=nRT;P总V=n总RT Pi → n=xi n总 → P=x,P总
由于 PiV= niRT; P总V= n总RT i i x n n P Pi = = 总 总 Pi = xi P总

口三、气体扩散定律 英国物理学家格拉罕姆(Graham) 指出:同温同压 下,气体的扩散速度与共密度的平方根成正比 即 4 B 或 uB A PM 由于p= A M B RT MA 无机化学
无机化学 三、气体扩散定律 英国物理学家格拉罕姆(Graham)指出:同温同压 下,气体的扩散速度与共密度的平方根成正比 i ui 1 A B B A u u 或 = RT PM = 即 由于 A B B A M M u u =

气体扩散定律的获得 无机化学
无机化学 气体扩散定律的获得

2.1.2 气体分子运动 设容器内有N个 质量为m的气体 分子。 一个分子沿X轴运 动碰撞A壁,由于 A 碰撞时无能量损 失, X 大小不变。 心L子
无机化学 2.1.2 气体分子运动 A z y x 设容器内有N个 质量为m的气体 分子。 一个分子沿X轴运 动碰撞A壁,由于 碰撞时无能量损 失, 大小不变。 2 u

每次碰撞,分子动量改变值为 -mN7-mV匠=-2m2 分子每秒碰撞A壁次数为V/I 该分子每秒钟动量总改变值为-2m(N)21 而该分子施于A壁的压力为 2mN元)211 容器内有N个分子,各面器壁共受力为 2NmN)211
每次碰撞,分子动量改变值为 2 2 2 − m u − −m u = −2m u 分子每秒碰撞A壁次数为 u / l 2 该分子每秒钟动量总改变值为 2m( u ) /l 2 2 − 而该分子施于A壁的压力为 2m( u ) /l 2 2 容器内有N个分子,各面器壁共受力为 2Nm( u ) /l 2 2