
§3 溶胶的动力性质 ·Brown运动 •胶粒的扩散 ·沉降平衡 ·高度分布定律
§3 溶胶的动力性质 • Brown 运动 • 胶粒的扩散 • 沉降平衡 • 高度分布定律

Brown运动(Brownian motion) 1827年植物学家布朗(Brown)用显微镜 观察到悬浮在液面上的花粉粉未不断地作不规 则的运动。 后来又发现许多其它物质如煤、 化石、 金属等的粉未也都有类以的现象。人们称微 粒的这种运动为布朗运动
Brown运动 (Brownian motion) 1827 年植物学家布朗(Brown)用显微镜 观察到悬浮在液面上的花粉粉末不断地作不规 则的运动。 后来又发现许多其它物质如煤、化石、 金属等的粉末也都有类似的现象。人们称微 粒的这种运动为布朗运动
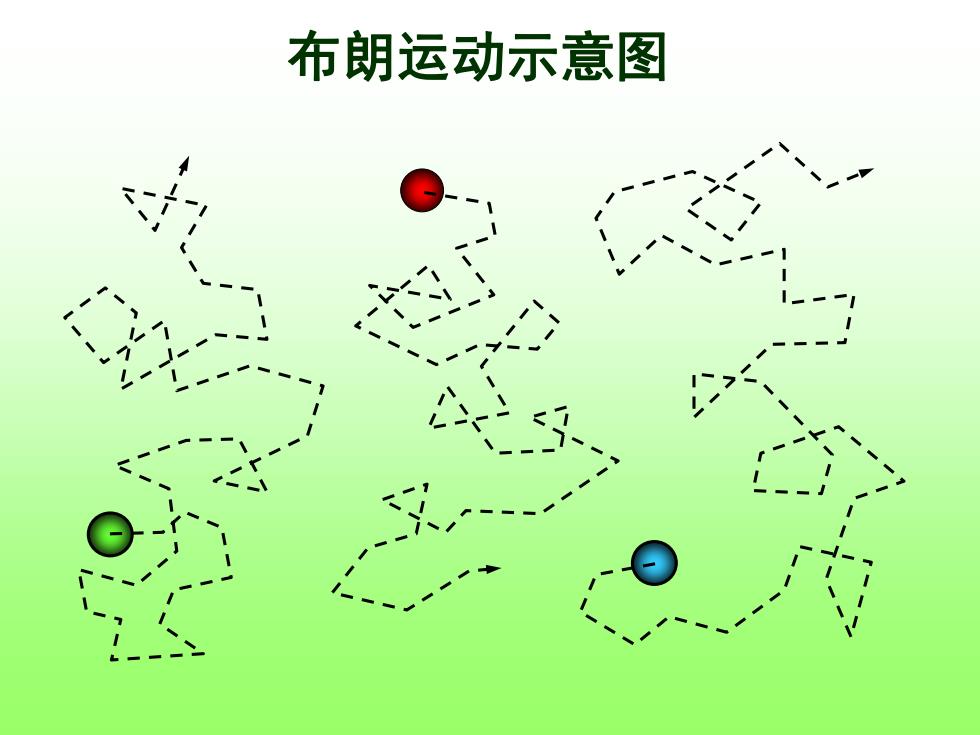
布朗运动示意图
布朗运动示意图

Brown运s动Brownian motion) 1903年发明了超显微镜,为研究布朗运动 提供了物质条件。 用超显微镜可以观察到溶胶粒子不断地作 不规则“之”字形的运动,从而能够测出在一 定时间内粒子的平均位移。 通过大量观察,得出结论:粒子越小,布 朗运动越激烈。其运动激烈的程度不随时间而 改变,但随温度的升高而增加
Brown运动(Brownian motion) 1903年发明了超显微镜,为研究布朗运动 提供了物质条件。 用超显微镜可以观察到溶胶粒子不断地作 不规则“之”字形的运动,从而能够测出在一 定时间内粒子的平均位移。 通过大量观察,得出结论:粒子越小,布 朗运动越激烈。其运动激烈的程度不随时间而 改变,但随温度的升高而增加

Brown运动的本质 1905年和1906年爱因斯坦(Einstein)和斯莫鲁 霍夫斯基(Smoluchowski)分别阐述了Brown运动的 本质。 认为Brownj运动是分散介质分子以不同大小和不同 方向的力对胶体粒子不断撞击而产生的,由于受到 的力不平衡,所以连续以不同方向、不同速度作不 规则运动。随着粒子增大,撞击的次数增多,而作 用力抵消的可能性亦大。 当半径大于5m,Brown:运动消失
Brown运动的本质 1905年和1906年爱因斯坦(Einstein)和斯莫鲁 霍夫斯基(Smoluchowski)分别阐述了Brown运动的 本质。 认为Brown运动是分散介质分子以不同大小和不同 方向的力对胶体粒子不断撞击而产生的,由于受到 的力不平衡,所以连续以不同方向、不同速度作不 规则运动。随着粒子增大,撞击的次数增多,而作 用力抵消的可能性亦大。 当半径大于5 m,Brown运动消失
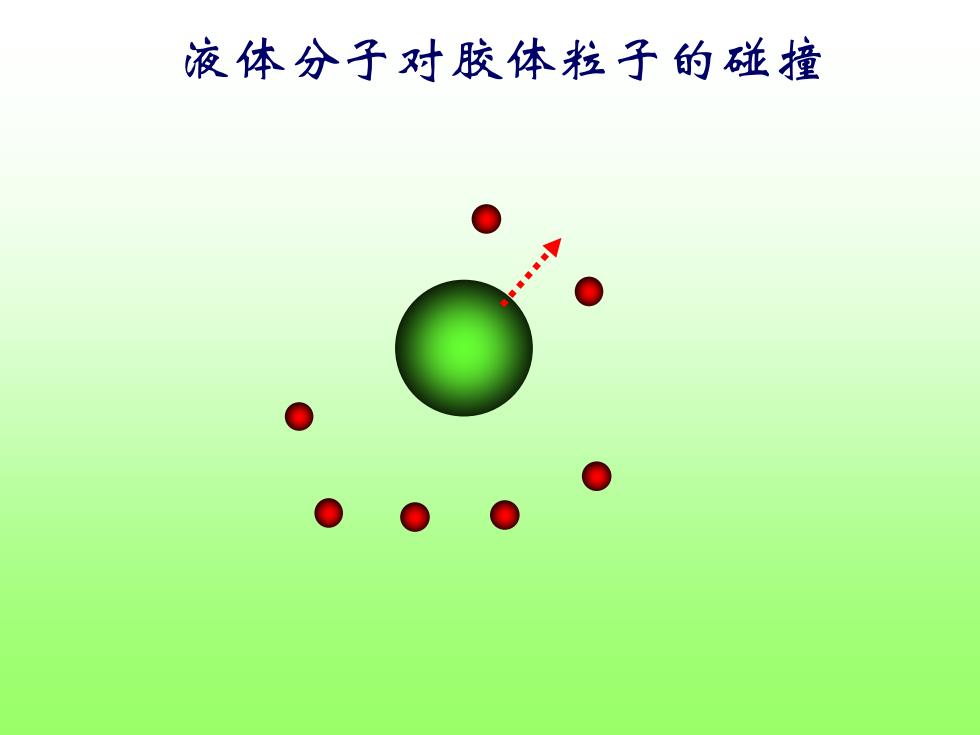
液体分子对胶体粒子的碰撞
液体分子对胶体粒子的碰撞

Brown:运动的本质 Einstein认为,溶胶粒子的Browni运动与分子运动类 似,平均动能为二k。并假设粒子是球形的,运用分子运 动论的一些基本概念和公式,得到Browni运动的公式为: RT 无规则≠无规律 N43π 式中x是在观察时间内粒子沿轴方向的平均位移; 为胶粒的半径;为介质的粘度;N4为阿伏加德罗常数。 这个公式把粒子的位移与粒子的大小、介质粘度、温 度以及观察时间等联系起来,也称爱因斯坦公式
Brown运动的本质 Einstein认为,溶胶粒子的Brown运动与分子运动类 似,平均动能为 。并假设粒子是球形的,运用分子运 动论的一些基本概念和公式,得到Brown运动的公式为: 3 2 kT 式中 x 是在观察时间t内粒子沿x轴方向的平均位移; r为胶粒的半径; 为介质的粘度; NA为阿伏加德罗常数。 3 A RT t x N r = 这个公式把粒子的位移与粒子的大小、介质粘度、温 度以及观察时间等联系起来,也称爱因斯坦公式。 无规则无规律

2、胶粒的扩散 胶粒也有热运动,因此也具有扩散现象。 只是溶胺的浓度较稀,胶粒不稳定,故这种现 象不显著。 由于分子的热运动和胶粒的布朗运动,使 溶胶粒子从高浓度区间向低浓度区间迁移的现 象称为胶粒的扩散作用。 溶胶粒子的扩散现象服从斐克第一定律 (Fick's first law)
2、胶粒的扩散 胶粒也有热运动,因此也具有扩散现象。 只是溶胶的浓度较稀,胶粒不稳定,故这种现 象不显著。 由于分子的热运动和胶粒的布朗运动,使 溶胶粒子从高浓度区间向低浓度区间迁移的现 象称为胶粒的扩散作用。 溶胶粒子的扩散现象服从斐克第一定律 (Fick’s first law)
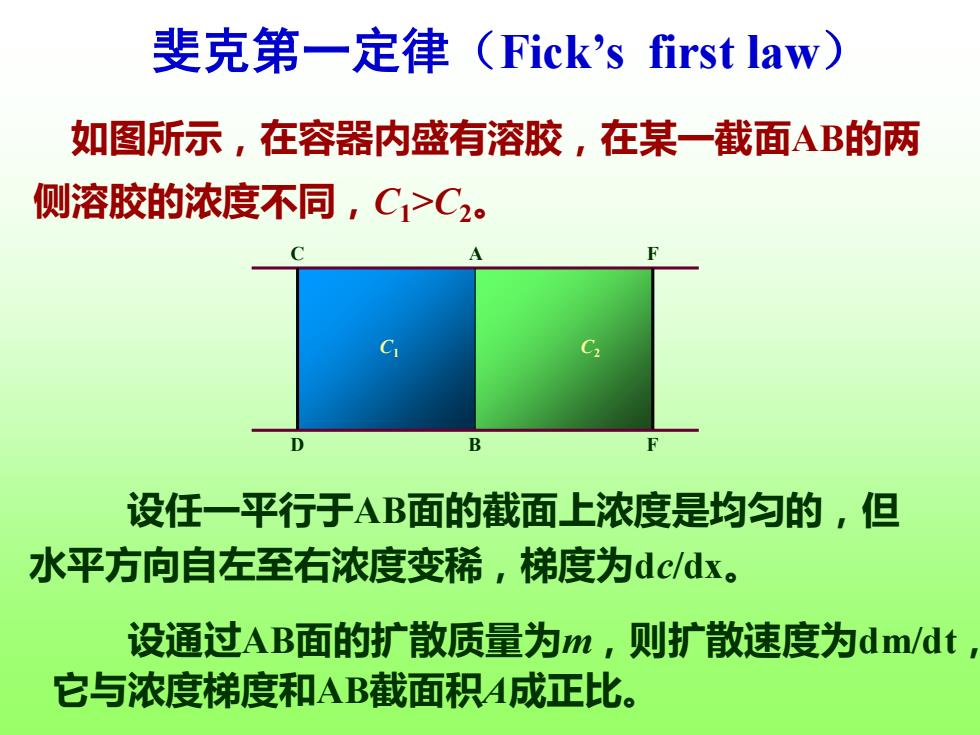
斐克第一定律(Fick's first law) 如图所示,在容器内盛有溶胶,在某一截面AB的两 侧溶胶的浓度不同,C1>C2。 A C D B 设任一平行于AB面的截面上浓度是均匀的,但 水平方向自左至右浓度变稀,梯度为dcdx。 设通过AB面的扩散质量为m,则扩散速度为dm/dt 它与浓度梯度和AB截面积A成正比
设通过AB面的扩散质量为m,则扩散速度为dm/dt, 它与浓度梯度和AB截面积A成正比。 斐克第一定律(Fick’s first law) 设任一平行于AB面的截面上浓度是均匀的,但 水平方向自左至右浓度变稀,梯度为dc/dx。 如图所示,在容器内盛有溶胶,在某一截面AB的两 侧溶胶的浓度不同,C1>C2。 A B C D F F C1 C2

斐克第一定律(Fick's first law) 用公式表示为: dm =-DA dc dt dx 这就是斐克第一定律。 式中D为扩散系数,其物理意义为:单位浓度梯度、 单位时间内通过单位截面积的质量。 式中负号表示扩散发生在浓度降低的方向, dc dm 0。 dx
斐克第一定律(Fick’s first law) 这就是斐克第一定律。 式中D为扩散系数,其物理意义为:单位浓度梯度、 单位时间内通过单位截面积的质量。 式中负号表示扩散发生在浓度降低的方向, 0。 d d c x d d m t d d = - d d m c DA t x 用公式表示为: