
§3强电解质溶液理论简介 平均活度和平均活度系数 离子强度 强电解质溶液的离子互吸理论
§3 强电解质溶液理论简介 平均活度和平均活度系数 离子强度 强电解质溶液的离子互吸理论

强电解质溶液的活度和活度系数 理想溶液组分B化学势的表示式: me UB=B (T)+RT In 非理想溶液组分B化学势的表示式 =)+RT Inam天(+K心 式中agm=Ymm° YBm→1 当溶液很稀,可看作是理想溶液,YB,m→1,则: B
强电解质溶液的活度和活度系数 理想溶液组分B化学势的表示式: B B B ( ) ln o o m T RT m = + 非理想溶液组分B化学势的表示式 B B B B, ( ) ln o m o m T RT m = + B B, ( ) ln o = + T RT a m B B, B, m m o m a m 式中 = 当溶液很稀,可看作是理想溶液,B,m→1,则: B, 1 m → B B,m o m a m

强电解质溶液的活度和活度系数 对强电解质: (1)强电解质几乎完全电离成离子,整体电解质 不复存在,其浓度与活度的简单关系不再适用: (2)与极稀的非电解质溶液可视作理想(稀)溶液, 活度系数近似等于1不同,对极稀的强电解质溶液, 由于离子间的相互作用,使它比非电解质溶液的 情况复杂得多,此时的活度与理想(稀)溶液的活度 仍有一定的偏差
强电解质溶液的活度和活度系数 对强电解质: (1)强电解质几乎完全电离成离子,整体电解质 不复存在,其浓度与活度的简单关系不再适用; (2)与极稀的非电解质溶液可视作理想(稀)溶液, 活度系数近似等于1不同,对极稀的强电解质溶液, 由于离子间的相互作用,使它比非电解质溶液的 情况复杂得多,此时的活度与理想(稀)溶液的活度 仍有一定的偏差

强电解质溶液的活度和活度系数 对任意价型电解质 M.A→y,M++yA 电解质的化学势e=g(T)+RTInaB 正离子的化学势4=,(T)+RTIna 负离子的化学势4=°(T)+RTIna. 电解质的化学势为所有正、负离子的化学势之和,即 B=VL4+VL=(y,+y_°)+RTln(a·a) =g+RTln(a·a') 比较电解质化学势的表示式,有a3=a必
强电解质溶液的活度和活度系数 对任意价型电解质 + + M A M A + z z − − → + − B + = + + − − B B B ( ) ln o = + T RT a + + + ( ) ln ( ) ln o o T RT a T RT a − − − = + = + ( ) ln( ) o o RT a a + − = + + + + − − + − B ln( ) o RT a a + − = + + − 电解质的化学势 正离子的化学势 负离子的化学势 电解质的化学势为所有正、负离子的化学势之和,即 B a a a + − 比较电解质化学势的表示式,有 = + −

平均活度和平均活度系数 正负离子总是成对出现,单个离子的a4,不易直接测出。 定义离子平均活度(mean activity of ions) ader(ar-avw V-V+V 在电解质化学势的表示式中,用离子平均活度分 别替代正、负离子的活度系数,则可用离子平均活度 求出电解质的化学势: uB =vu +vu =v.(u+RTIna.)+v(u+RTIna) =v (u+RTIna.)+v(u+RTIna
正负离子总是成对出现,单个离子的a+(-) ,不易直接测出。 平均活度和平均活度系数 1 + def = a a a ( ) + + − − + − 定义离子平均活度(mean activity of ions) ( ln ) ( ln ) ( ln ) ( ln ) B o o o o RT RT a a R R T T a a + + − − + + − − + + − − − + = + = + + + = + + + 在电解质化学势的表示式中,用离子平均活度分 别替代正、负离子的活度系数,则可用离子平均活度 求出电解质的化学势:

类似的,定义 离子平均活度系数(mean activity coefficient of ions) def( 离子平均质量摩尔浓度(mean molality of ions) m4dcf(mm)% 易推导得到如下结果: =aa心=ag=(0y:%》
类似的,定义 1 def ( ) + − + − 离子平均活度系数(mean activity coefficient of ions) 1 def m m m ( ) + − + − 离子平均质量摩尔浓度(mean molality of ions) o m a m = ( ) o m m = B a a a a + − + − = = 易推导得到如下结果:

例:写出CuS04,K2SO4与A2S04)3离子平均浓度与 电解质浓度的关系 CuSO mce =m,mso=m,V.=v =1,v=V,+v=2 m:=(m·m)=m NaSO,:myo =2m,msor=m,v,=2,v.=1,v=V+v=3 m=(mmt)=[(2m'm]=4.m 4,(S04)3:mo=2m,mo2=3m,V,=2,.=3,v=+业.=5 %=(mm)=[(2m-(3m)]=108.m
例:写出CuSO4,K2SO4与Al2 (SO4 )3离子平均浓度与 电解质浓度的关系 ( ) 2 2 4 4 + + 1 / : , , 1, 2 Cu SO CuSO m m m m m m m m + − + − + − − − = = = = = + = = = ( ) ( ) 2 4 2 4 + + 1 / 1/3 2 1/3 : 2 , , 2, 1, 3 2 4 Na SO Na SO m m m m m m m m m m + − + − + − − − = = = = = + = = = = ( ) ( ) ( ) ( ) 2 4 2 4 + + 3 1 / 1/5 2 3 1/5 : 2 , 3 , 2, 3, 5 2 3 108 Na SO Al SO m m m m m m m m m m + − + − + − − − = = = = = + = = = =

计算m=1.20 mol kg1的MgCL2水溶液在298K时的电解质活 度已知Y=0.630. 解:先求平均浓度与电解质浓度的关系 mus=m,mcr =2m,V.=1,v=2,v=v,+v=3 m=(m)=[m-(2m)2]=43.m a±=y±·m4/m°=0.630×43×1.20=1.20 aB=a=1.203=1.73
解:先求平均浓度与电解质浓度的关系 ( ) ( ) 2 + + 1 / 1/3 2 1/3 1/3 3 , 2 , 1, 2, 3 2 4 / 0.630 4 1.20 1.20 1.20 1.73 Mg Cl o B m m m m m m m m m m a m m a a + − + − + − − − = = = = = + = = = = = = = = = = 计算 m=1.20 mol kg-1的MgCl2水溶液在298K时的电解质活 度已知 0.630 . =
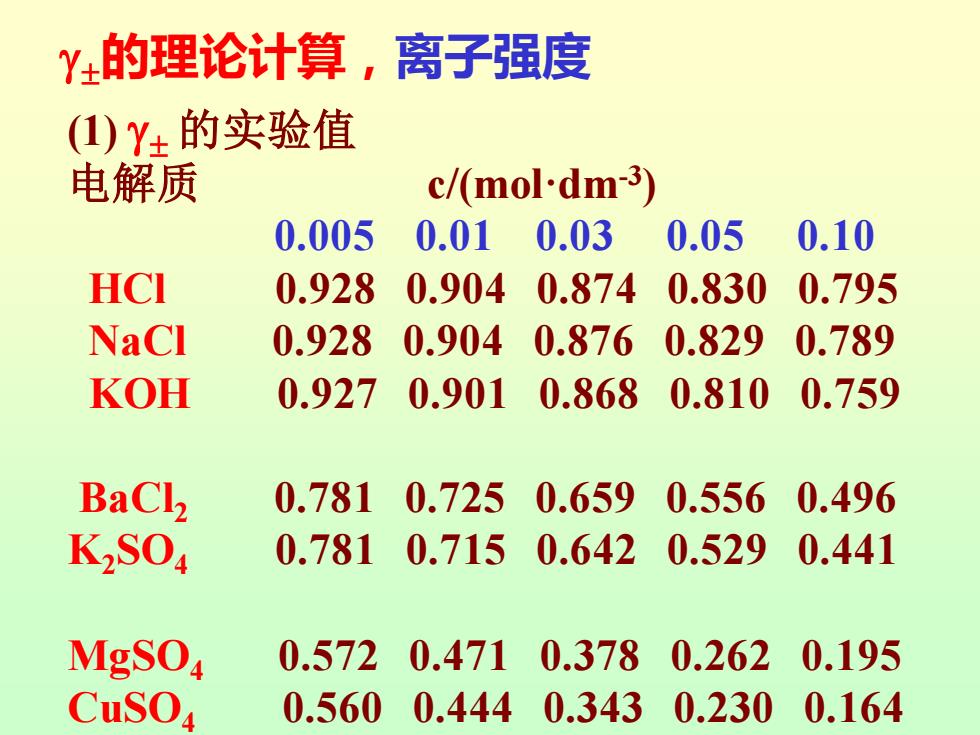
Y±的理论计算,离子强度 (1)Y±的实验值 电解质 c/(mol-dm-3) 0.005 0.01 0.03 0.05 0.10 HCI 0.928 0.9040.874 0.830 0.795 NaCl 0.928 0.904 0.876 0.829 0.789 KOH 0.927 0.9010.8680.810 0.759 BaCl2 0.7810.725 0.6590.556 0.496 K2S04 0.7810.7150.6420.5290.441 MgSO 0.572 0.4710.378 0.262 0.195 CuSO 0.5600.444 0.3430.2300.164
(1) 的实验值 电解质 c/(mol·dm-3 ) 0.005 0.01 0.03 0.05 0.10 HCl 0.928 0.904 0.874 0.830 0.795 NaCl 0.928 0.904 0.876 0.829 0.789 KOH 0.927 0.901 0.868 0.810 0.759 BaCl2 0.781 0.725 0.659 0.556 0.496 K2SO4 0.781 0.715 0.642 0.529 0.441 MgSO4 0.572 0.471 0.378 0.262 0.195 CuSO4 0.560 0.444 0.343 0.230 0.164 的理论计算,离子强度

离子强度 从实验结果看出,影响离子平均活度系数的主 要因素是电解质的总浓度和离子的价数,而价数的 影响更显著。 据此Lewis和Randall提出了离子强度(ionic strength)的概念。溶液的离子强度定义为离子浓 度与其价数的平方乘积总和的一半,写作 1=2∑mz 式中是溶液中离子的真实质量摩尔浓度,如果是 弱电解质则应由其相应的电离度求得;z是离子的价 数。离子强度的量纲与m相同
离子强度 2 i i i 1 2 I m z = 式中mi是溶液中i离子的真实质量摩尔浓度,如果是 弱电解质则应由其相应的电离度求得;zi是离子的价 数。离子强度I的量纲与m相同。 从实验结果看出,影响离子平均活度系数的主 要因素是电解质的总浓度和离子的价数,而价数的 影响更显著。 据此Lewis和Randall提出了离子强度(ionic strength)的概念。溶液的离子强度I定义为离子浓 度与其价数的平方乘积总和的一半,写作 I