
传递现象 (Transport Phenomenon 扩散(Diffusion) 一一物质传递 C1 c2 热传导(Thermal Conduction) 一一热量传递 T2 粘滞性(Viscosity) 一一动量传递
传递现象 (Transport Phenomenon) 扩散(Diffusion) --物质传递 热传导(Thermal Conduction) --热量传递 粘滞性(Viscosity) --动量传递
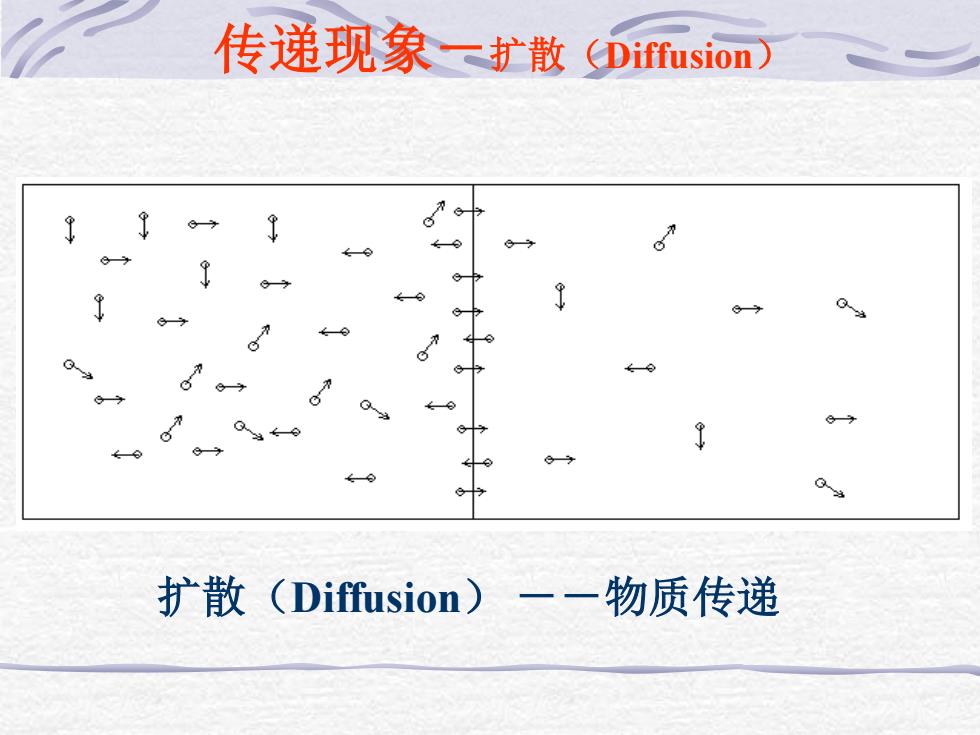
传递现象一扩散(Diffusion) ← 扩散(Diffusion)一一物质传递
传递现象-扩散(Diffusion) 扩散(Diffusion) --物质传递
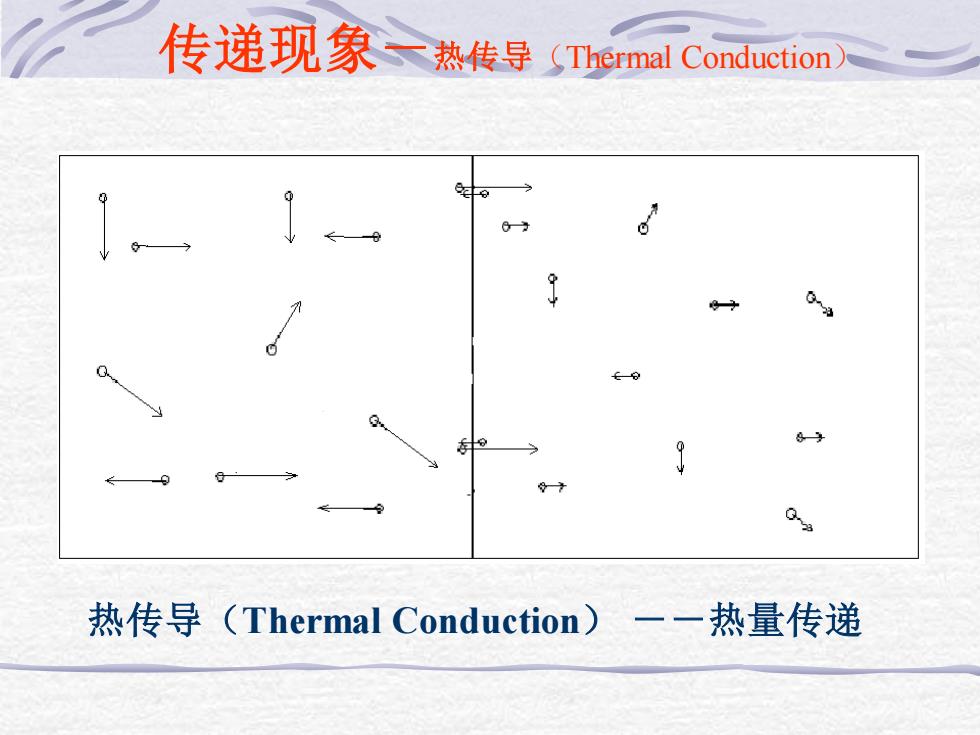
传递现象三热传导 (Thermal Conduction fo 热传导(Thermal Conduction)一一热量传递
传递现象-热传导(Thermal Conduction) 热传导(Thermal Conduction) --热量传递
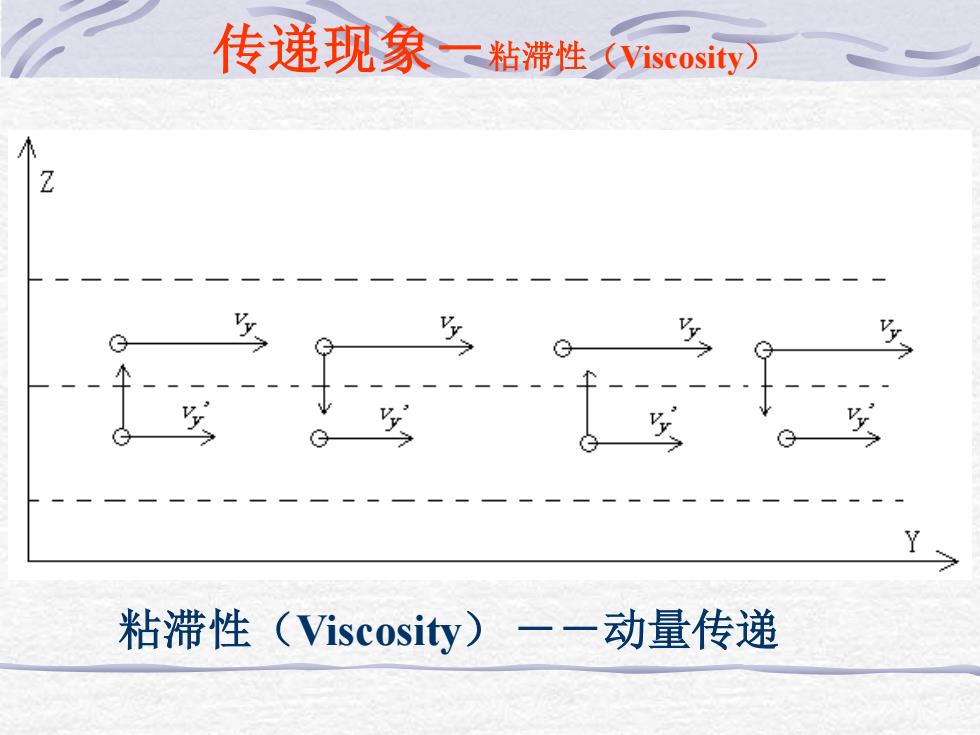
传递现象二粘滞性(Viscosity 粘滞性(Viscosity)一一动量传递
粘滞性(Viscosity) --动量传递 传递现象-粘滞性(Viscosity)

传递现象 (Transport Phenomenon) 总结: 1.从微观成因看,物质传递、热量传递和动量 传递都是由于分子的无规则热运动引起的, 是大量分子热运动的统计平均行为。为与因 流体整体运动引起的传递相区分,我们称上 述三种传递现象为分子传递现象
传递现象 (Transport Phenomenon) 总结: 1. 从微观成因看,物质传递、热量传递和动量 传递都是由于分子的无规则热运动引起的, 是大量分子热运动的统计平均行为。为与因 流体整体运动引起的传递相区分,我们称上 述三种传递现象为分子传递现象

传递现象 (Transport Phenomenon) 2.三种传递现象具有类似的唯象规律 以“通量”或“流”表示传递的速率,其量纲为 [物质的量 [热量」·[面积]-1.时间]1 [动量】 引起传递的宏观原因为“梯度”或称之为“力”, 其量纲为 【浓度】 [ 温度】·长度]1 [速度」
传递现象 (Transport Phenomenon) 2. 三种传递现象具有类似的唯象规律 以“通量”或“流”表示传递的速率,其量纲为 [物质的量] [ 热 量 ] [面积]-1 [时间]-1 [ 动 量 ] 引起传递的宏观原因为“梯度”或称之为“力”, 其量纲为 [ 浓 度 ] [ 温 度 ] [长度]-1 [ 速 度 ]

传递现象 (Transport Phenomenon) 通量与梯度之间存在着函数关系,这一关系是传递现 象动力学的基本关系式。 J=f(X) 在梯度不大的情况下,三种传递现象的通量与梯度 之间均为正比关系。 J=k·X
传递现象 (Transport Phenomenon) 通量与梯度之间存在着函数关系,这一关系是传递现 象动力学的基本关系式。 J f X = ( ) 在梯度不大的情况下,三种传递现象的通量与梯度 之间均为正比关系。 J k X =

费克定律(Fick's Law) 一、费克定律(Fick'sLaw) 1o-Dad dcB dz j为物质通量,即单位时间通过单位面积的物质B的数量, 量纲为mol·m2.s1 DBA为扩散系数,完整的说是B在A一B二元体系中的扩散系数 量纲为m2.s1 负号表明扩散方向与梯度方向相反
费克定律(Fick’s Law) 一、费克定律(Fick’s Law) B Bz BA dc j D dz = − jBz为物质通量,即单位时间通过单位面积的物质B的数量, 量纲为 mol m-2 s -1 DBA为扩散系数,完整的说是B在A-B二元体系中的扩散系数 量纲为 m2 s -1 负号表明扩散方向与梯度方向相反

傅立叶定律(Fourier'sLaw) 二、傅立叶定律(Fourier'sLaw) dT 92=-. dz q为热通量,即单位时间通过单位面积的热量, 量纲为J·m2·sl 几为导热系数或称热导率,量纲为J·K1·ml·sl
傅立叶定律( Fourier’s Law ) 二、傅立叶定律(Fourier’s Law) z dT q dz = − qz为热通量,即单位时间通过单位面积的热量, 量纲为 J m-2 s -1 为导热系数或称热导率,量纲为 J K-1 m-1 s -1

牛顿定律(Newton'SLaW) 三、牛顿定律(Newton'sLaw dv. =-7 y dz P为动量通量,即单位时间沿着方向通过单位平面的动量(y 方向),量纲为kg·ml.s2也可表示为Nm2 动量通量即为各层流体间的内摩擦力,称之为剪切应力,。 牛顿定律也可表示为 y=± dvy dz n为粘度或称动力粘度,量纲为N·m2.s或Pa·s 过去常用泊(poise)或厘泊(cp),Icp=1X103Pa·s
牛顿定律(Newton’s Law) 三、牛顿定律(Newton’s Law) y zy dv P dz = − Pzy为动量通量,即单位时间沿着z方向通过单位平面的动量(y 方向),量纲为kg m-1 s -2 也可表示为 N m-2 为粘度或称动力粘度,量纲为N m-2 s 或 Pa s 过去常用泊(poise )或厘泊(cp),1 cp =1×10-3 Pa s 动量通量即为各层流体间的内摩擦力,称之为剪切应力,zy 牛顿定律也可表示为 y zy dv dz =