
量子统计法 Boltzmann分布律
量子统计法 Boltzmann分布律

§4.量子统计法 自然界的微观粒子分为两大类: 玻色子(Bose particle): 不遵守保利不相容原理; 费米子(Fermi particle):遵守保利不相容原理, 一、Bose-Einstein统计: Bose子:一个量子态可容纳多个粒子 宏观体系的热力学平衡衡态拥有数目极其巨大 的微观运动状态。这些微观运动状态存在 于各种不同的分布中。 分布:在满足体系宏观条件(如U、V、T等) 的前提下,粒子在各能级上的分配方式
§4. 量子统计法 自然界的微观粒子分为两大类: 玻色子(Bose particle): 不遵守保利不相容原理; 费米子(Fermi particle): 遵守保利不相容原理. 一 、Bose-Einstein统计: Bose子:一个量子态可容纳多个粒子. 宏观体系的热力学平衡态拥有数目极其巨大 的微观运动状态。这些微观运动状态存在 于各种不同的分布中。 分布:在满足体系宏观条件(如U、V、T等) 的前提下,粒子在各能级上的分配方式

·设体系含N个玻色子,其在能级上的一种分布 是:(N,} 能级: ∈0∈1,∈i. 粒子数: No2 N12.,Ni. 条件: ∑iN∈:=E; ∑N=N W:分布{N:)具有的微观运动状态数目. ·首先求某一能级的不同微观状态数(即配容数): 设:能级的能量: 能级的简并度: 能级的粒子数: N
• 设体系含N个玻色子, 其在能级上的一种分布 是:﹛Ni﹜ 能级: ∈0 , ∈1 ,. , ∈i. 粒子数: N0 , N1 , . , Ni. 条件: ∑i Ni∈i = E; ∑i Ni = N W:分布﹛Ni﹜具有的微观运动状态数目. • 首先求某一能级的不同微观状态数(即配容数): 设: 能级的能量: ∈i 能级的简并度: gi 能级的粒子数: Ni
此状态数的求算是一排列组合问题: 共有g+N个无素,如图排列,方框代表量子态, 圆球表示微观粒子,方框后面的小球均处于此 方框所代表的量子态: 000▣000 g1种选择 (gi+Ni一1)!种选择 能级的配容数为g(g:+N;一1)!
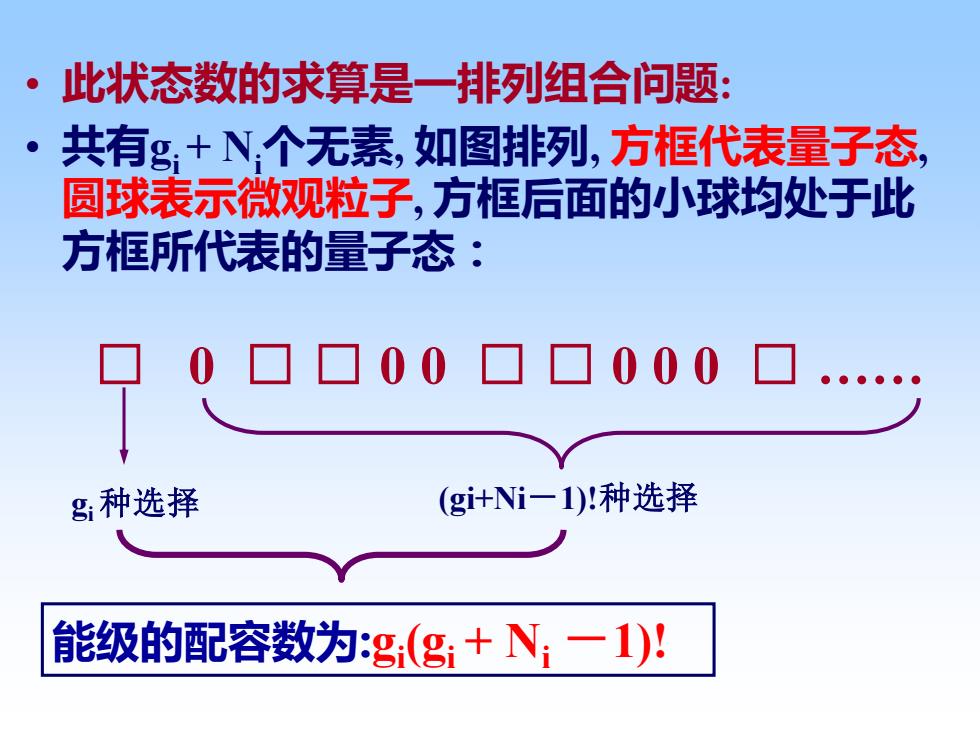
• 此状态数的求算是一排列组合问题: • 共有gi + Ni个无素, 如图排列, 方框代表量子态, 圆球表示微观粒子, 方框后面的小球均处于此 方框所代表的量子态: □ 0 □ □ 0 0 □ □ 0 0 0 □ . gi 种选择 能级的配容数为:gi (gi + Ni -1)! (gi+Ni-1)!种选择

量子态和粒子位置的交换不会产生新的态,故应对粒子 的全同性和量子态的位置无关性进行修正: W:=gg1+N;-1)!/(g)N)9 =g(g+N;-1)1/g(g:-1)N) =(g+N:-1)!/N)(g-1)9 分布(N,}拥有的量子态数为: W=ΠW,=ΠH(g+N:-1)/N(g-1)(I 体系拥有的量子态数为各种分布量子态数之和: -EW =Π(g+N-1)1/N,(g-1)] (2) EN=N N;∈=E
量子态和粒子位置的交换不会产生新的态, 故应对粒子 的全同性和量子态的位置无关性进行修正: Wi = gi (gi + Ni-1)! /(gi )!(Ni )! = gi (gi+ Ni-1)! / gi (gi-1)!(Ni )! = (gi + Ni-1)! / (Ni )!(gi-1)! 分布﹛Ni﹜拥有的量子态数为: W = iWi = i [(gi+Ni-1)! / Ni !(gi -1)!] (1) 体系拥有的量子态数为各种分布量子态数之和: Ω= ΣW =[i (gi+Ni -1)! / Ni !(gi -1)!] (2) ΣNi=N ΣNi∈i=E

在各分布中,必存在一种分布拥有的微观状态数最多,此分 布出现的几率最大,称为景可几分布.可以证明最可几分布 的粒子在能级上的分布公式: Ni*=g;/(ea+Bei-1) 3) B=1/kT; a由∑:N=N求出。 二、Fermi-Dirac统计 费米子遵守保利不相容原理,每个量子态只能容纳一个粒子. 设有如下分布: N ∈0···∈i· N0···N·· 满足: ∑N:=N ∑N,∈=E
在各分布中, 必存在一种分布拥有的微观状态数最多, 此分 布出现的几率最大, 称为最可几分布. 可以证明最可几分布 的粒子在能级上的分布公式: Ni * = gi /(eα+β∈i-1) (3) =1/kT; α由Σi Ni=N求出。 二、Fermi-Dirac统计 费米子遵守保利不相容原理,每个量子态只能容纳一个粒子. 设有如下分布: {Ni } ∈0﹒﹒﹒∈i﹒﹒﹒ N0 ﹒﹒﹒ Ni﹒﹒﹒ 满足: ΣiNi = N ΣiNi∈i = E

首先求能级的配容数W: W:=Cei=gNg-N识 分布N}拥有的状态数W为: W=ΠIg!N(g-N) (4) 体系拥有的微观状态数是各种分布之和: 2=W=ΠIg!N(g·N)I(5) 费米子的最可几分布由下式表示: N,=g;/(eatB∈i+1) (6) B=1/kT;a由N,=N可求出
首先求能级i的配容数Wi : Wi = Cgi Ni = gi ! /Ni !(gi-Ni )! 分布{Ni } 拥有的状态数W为: W = i [gi ! /Ni !(gi-Ni )!] (4) 体系拥有的微观状态数是各种分布之和: Ω=ΣW=[i [gi ! /Ni !(gi-Ni )!]] (5) 费米子的最可几分布由下式表示: Ni = gi /(eα+β∈i +1) (6) β=1/kT; α由Ni = N可求出

三、Boltzmann统计: 当g;>N:时:Bose-Einstein:统计 Fermi-Dirac统计 趋于同一极限 能级的量子态数: g>Ng>1.N+g-1≈g W:=(g:+N:-1)N(g一1)! =(g+N:-1)(g+N-2).g(g-1)1/Ng-1)1 =gg.g/Ng =gi Ni/N! (7) 分布N}的量子态数等于能级量子态数的乘积: W=Πi(g:i/N) (8) 体系拥有的种微观运动状态数为: EW (EN-N; N∈=E) (9)
三、Boltzmann统计: 当gi>> Ni时:Bose-Einstein统计 Fermi-Dirac 统计 趋于同一极限 能级的量子态数: ∵gi>>Ni,gi >>1 ∴Ni+ gi-1≈gi Wi = (gi + Ni-1)!/Ni !(gi-1)! = (gi + Ni-1)(gi + Ni-2).gi ·(gi -1)! / Ni !(gi -1)! = gi ·gi. gi / Ni ! = gi Ni / Ni ! (7) 分布{Ni } 的量子态数等于能级量子态数的乘积: W =∏i (gi Ni / Ni !) (8) 体系拥有的种微观运动状态数为: Ω= ΣW (ΣNi=N; ΣNii=E) (9)

求最可几分布: W=Π:(gNi/N) InW=>i(N,Ing;-N,InN;+N) (10) 令: f=InW=>(N;Ing;-N InN;+N)(11) y1=∑iN-N=0 (12) y2=∑iN∈:-E=0 (13) 拉格朗日条件极值: Of/ON;=Ing;-InN-N:/N;+1 =In(g;/N) 0y1/N:=1 50 0y2/N;=∈i (1
求最可几分布: W =∏i (gi Ni / Ni !) lnW=∑i (Ni lngi-Ni lnNi + Ni ) (10) 令: f =lnW=∑i (Ni lngi-Ni lnNi+ Ni ) (11) y1 = ∑i Ni-Ni = 0 (12) y2 = ∑i Ni∈i-E = 0 (13) 拉格朗日条件极值: ∂f/∂Ni=lngi-lnNi-Ni /Ni+1 =ln(gi /Ni ) (14) ∂y1 /∂Ni = 1 (15) ∂y2 /∂Ni = ∈i (16)

由拉格朗日条件极值求算法,将(15)式乘以常数o,(16) 式乘以常数(B),与(14)式相加,并令其为零: . lngN:+a-B∈=0 lng/N:=-+B∈i lnN/g:=u-B∈i N/g=eu-B∈i ∴.N=g:eu-BEi =g;'ea-∈ikT (17) o,B是待定常数.可由限定条件求出
由拉格朗日条件极值求算法, 将(15)式乘以常数, (16) 式乘以常数(-), 与(14)式相加, 并令其为零: ∴ lngi /Ni +α-β∈i= 0 lngi /Ni = -α+β∈i lnNi /gi =α-β∈i Ni /gi = e α-β∈i ∴ Ni * = gi·eα-β∈i = gi·eα-∈i/kT (17) , 是待定常数. 可由限定条件求出