
物 理 化 学 第二章例题
物 理 化 学 第 二 章 例 题
·例1.一理想气体体系由A点经绝热可逆过程到达C点,若体系从相同始点经 不可逆绝热过程达到具有相同未态体积的D点或具有相同未态压力的D'点, 请判断D或D’点在绝热曲线的哪一边? 解:体系由A点经绝热可逆膨胀沿 红线到达C点. 若经等温可逆膨胀将沿蓝线到B点或B'点. 若体系经不可逆绝热膨胀达到相同末态 体积的D点,D应在BC之间. 在相同的绝热条件下,可逆过程作最大功, 故绝热可逆过程体系温度下降幅度最大, B 其余绝热不可逆过程做功较少,降温幅度 较小,故达相同末态体积时,终点D必在C 等温线 点之上 P2 D 但绝热膨胀过程,多少需对外做功,体系 的温度多少有所下降,故D点不可能高于 等温过程的B点所以D点必在BC之间. 同理,绝热不可逆膨胀到具有相同末态 压力的D点,D点必在BC之间
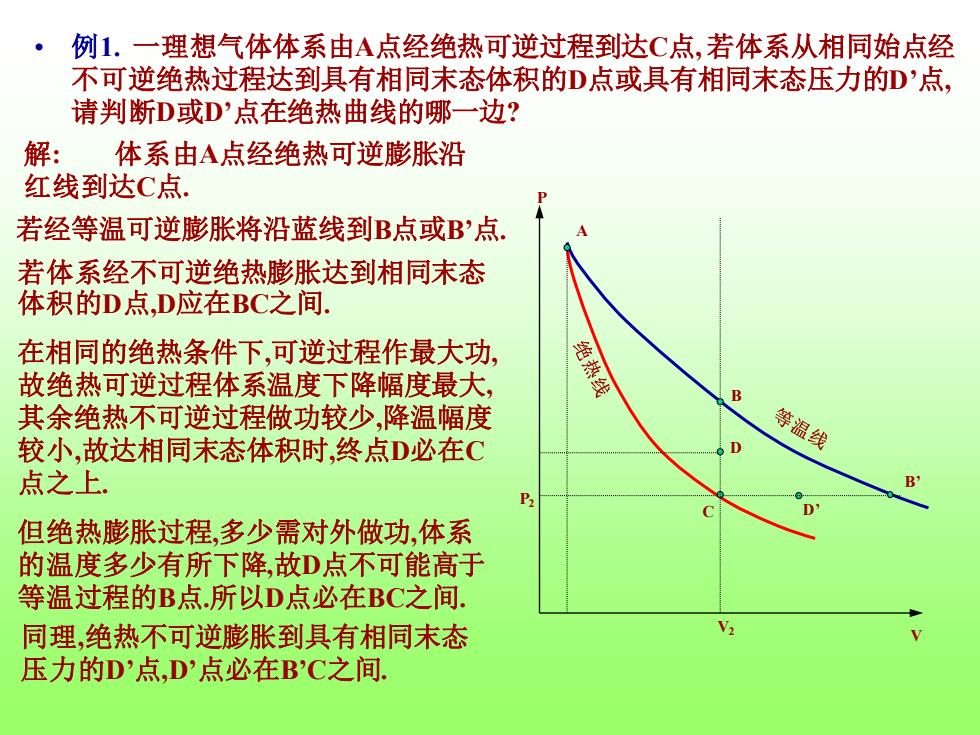
• 例1. 一理想气体体系由A点经绝热可逆过程到达C点, 若体系从相同始点经 不可逆绝热过程达到具有相同末态体积的D点或具有相同末态压力的D’点, 请判断D或D’点在绝热曲线的哪一边? P V D’ P2 B’ A C V2 B D 解: 体系由A点经绝热可逆膨胀沿 红线到达C点. 若经等温可逆膨胀将沿蓝线到B点或B’点. 若体系经不可逆绝热膨胀达到相同末态 体积的D点,D应在BC之间. 在相同的绝热条件下,可逆过程作最大功, 故绝热可逆过程体系温度下降幅度最大, 其余绝热不可逆过程做功较少,降温幅度 较小,故达相同末态体积时,终点D必在C 点之上. 但绝热膨胀过程,多少需对外做功,体系 的温度多少有所下降,故D点不可能高于 等温过程的B点.所以D点必在BC之间. 同理,绝热不可逆膨胀到具有相同末态 压力的D’点,D’点必在B’C之间

。 例2.300K下,1摩尔单原子分子理想气体由10升经如下过程膨胀到20升. ()等温可逆膨胀;2)向真空膨胀;(3)等温恒外压(末态压力)膨胀.求上述 各过程的Q,W,△U,△H,△S,△F,和△G? ·解:(1)理想气体等温过程:△U=0△H=0 Q=W=nRT1n(V,V)=8.314:300ln(20/10)=1729J ΔS=nRIn(V2/V)=8.314ln2=5.763J/K ● △F=△(G-pV=△G-△(pV=△G (pV)m=nRT=常数 AG=nRTIn(V/V2)=-1729 J (2) ·过程(2)与过程()具有相同的始末态,故状态函数的改变值相 △U=0△H=0△S=5.763J/K △F=△G=-1729J ,外压为零 O=W=0 3),·过程3)与过程(①具有相同的始末态,故状态函数的改变值相 △U=0△H=0△S=5.763J/K△F=△G=-1729J Q-W=p外dV=p2(V2V) p1V1p2V2=RTP2=RT/V2=8.314300/0.02=124710Pa W=124710(0.02-0.01)=1247J 0=1247J
• 例2. 300K下,1摩尔单原子分子理想气体由10升经如下过程膨胀到20升. (1) 等温可逆膨胀; (2) 向真空膨胀; (3) 等温恒外压(末态压力)膨胀. 求上述 各过程的Q,W,U,H,S,F,和G? • 解: (1) 理想气体等温过程: U=0 H=0 • Q=W=nRTln(V2 /V1 )=8.314·300·ln(20/10)=1729 J • S=nRln(V2 /V1 )=8.314·ln2=5.763 J/K • F=(G-pV)= G-(pV)=G (pV)T=nRT=常数 • G=nRTln(V1 /V2 )=-1729 J • (2) ∵ 过程(2)与过程(1)具有相同的始末态,故状态函数的改变值相 • U=0 H=0 S=5.763J/K F=G=-1729J • ∵ 外压为零 ∴ Q=W=0 • (3) ∵ 过程(3)与过程(1)具有相同的始末态,故状态函数的改变值相 • U=0 H=0 S=5.763J/K F=G=-1729J • Q=W=∫p外dV=p2 (V2 -V1 ) • p1V1=p2V2=RT p2=RT/V2=8.314·300/0.02=124710 Pa • W=124710(0.02-0.01)=1247 J • Q=1247 J

。 例3.设某物体A的温度为T,热容为C,另有一无穷大冷源温度为T,有一可 逆热机在此物体与冷源间循环运行,热机从物体A吸热作功.试求,当物体的 温度降为T时,热机所作的功,以及物体传给冷源的热量? 。 解:设热机在物体与冷源之间可逆地工作,每次从A吸收热量δQ1,对外作功 δW,并传递给冷源δQ2的热量.每循环一次,A的温度会降低dT,如此循环不已, 直至物体A的温度降至冷源的温度T为止、 δQ=-CdT (.dT<0,又吸热为正) 令物体A的温度为T,T是变化的. n=8W/8Q=(T-To)/T=1-To/T δW=mδQ=-CdT(1-TW/T)F-CdT+CTodlnT W=TrT0[-CdT+CTodlnT]=-C(To-T)+CToln(To/T1) W=C(T-To)-CToln(T/To) Q=-JCdT=C(T-To) Q2=W-Q1=-CToln(T/To) m=W/Qi=IC(Ti-To)-CToln(T/To)l/C(T-To)=1-Toln(T /To)/(T-To) 。 绝热作的功为: C[(TI-To)-Toln(T/To)]; ·传递给冷源的热量为: -CToln(T/To); ·热机的总效率为: 1-[Toln(T/To)/(T-To]
• 例3. 设某物体A的温度为T1 ,热容为C,另有一无穷大冷源温度为T0 . 有一可 逆热机在此物体与冷源间循环运行,热机从物体A吸热作功. 试求,当物体的 温度降为T0时,热机所作的功,以及物体传给冷源的热量? • 解: 设热机在物体与冷源之间可逆地工作,每次从A吸收热量Q1 ,对外作功 W,并传递给冷源Q2的热量. 每循环一次,A的温度会降低dT,如此循环不已, 直至物体A的温度降至冷源的温度T0为止. • Q1=-CdT (∵ dT<0, 又吸热为正) • 令物体A的温度为T,T是变化的. • = W/Q1=(T-T0 )/T=1-T0 /T • W=Q1=-CdT(1-T0 /T)=-CdT+CT0dlnT • W=∫T1 T0[-CdT+CT0dlnT]=-C(T0 -T1 )+CT0 ln(T0 /T1 ) • W=C(T1 -T0 )-CT0 ln(T1 /T0 ) • Q1=-∫CdT=C(T1 -T0 ) Q2= W-Q1 =-CT0 ln(T1 /T0 ) • 总=W/Q1=[C(T1 -T0 )-CT0 ln(T1 /T0 )]/C(T1 -T0 )=1-T0 ln(T1 /T0 )/(T1 -T0 ) • 绝热作的功为: C[(T1 -T0 )-T0 ln(T1 /T0 )]; • 传递给冷源的热量为: -CT0 ln(T1 /T0 ); • 热机的总效率为: 1-[T0 ln(T1 /T0 )/(T1 -T0 )]

。 例4.下式为一气体定律的形式:pfV)=RT fV)是V的任意 连续函数,试证明:凡服从此方程的气体都有:(U/V)1=0? ·解:有公式: (aU/o)=T(p/oT)y-p (1) 由题给条件: ● p=RT/f(V) (ap/aT)v=R/f(V) (2) ·将2)式代入(1)式: (oU/av)=TR/f(V)-p=p-p=0 证毕
• 例4.下式为一气体定律的形式: pf(V)=RT f(V)是V的任意 连续函数,试证明: 凡服从此方程的气体都有:(U/V)T=0? • 解: 有公式: • (U/V)T=T(p/T)V-p (1) • 由题给条件: • p=RT/f(V) • (p/T)V=R/f(V) (2) • 将(2)式代入(1)式: • (U/V)T=TR/f(V) -p=p-p=0 • 证毕
·例5.400K的恒温槽传4000J的热量给环境(300K,求△S? ·解:△S=△S体+△S环 △S体=QR/T体=-4000/400=-10J/K △S环=-Q/T环=4000/300=13.33J/K ● △S=△S体+AS环=3.33J/K>0为不可逆过程. 此题应设计一可逆途径求算,可逆途径可设计为图: 400K国 400K-dI 300K+dT 300K
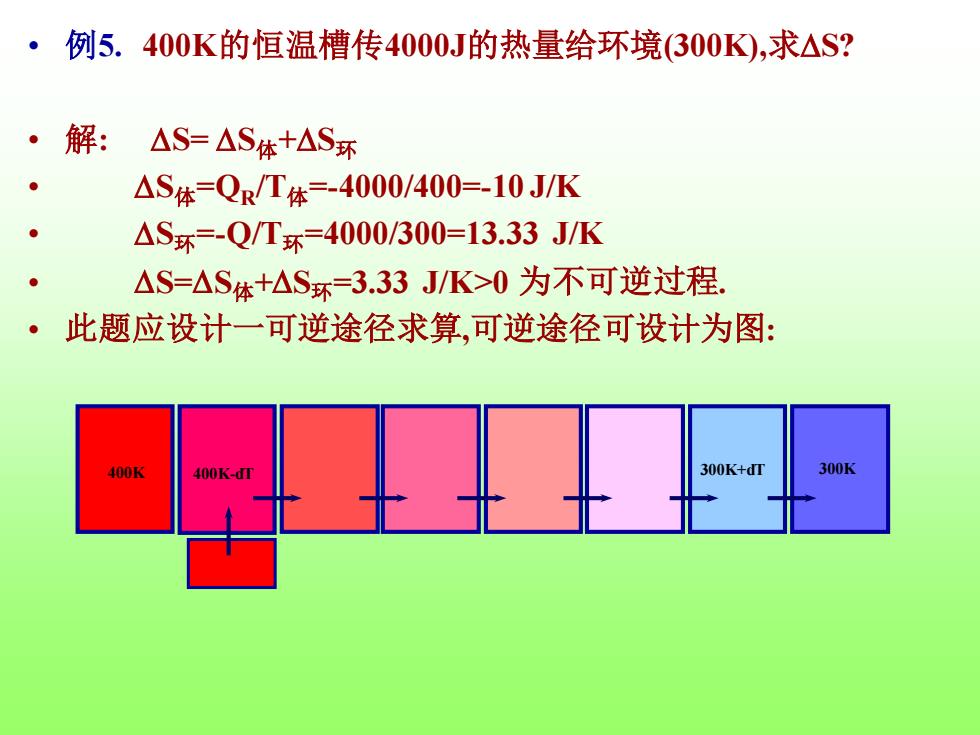
• 例5. 400K的恒温槽传4000J的热量给环境(300K),求S? • 解: S= S体+S环 • S体=QR/T体=-4000/400=-10 J/K • S环=-Q/T环=4000/300=13.33 J/K • S=S体+S环=3.33 J/K>0 为不可逆过程. • 此题应设计一可逆途径求算,可逆途径可设计为图: 400K 400K 300K+dT -dT 300K
400K 4000J,可逆热传导 1000J 3000J 300K 磨擦生热
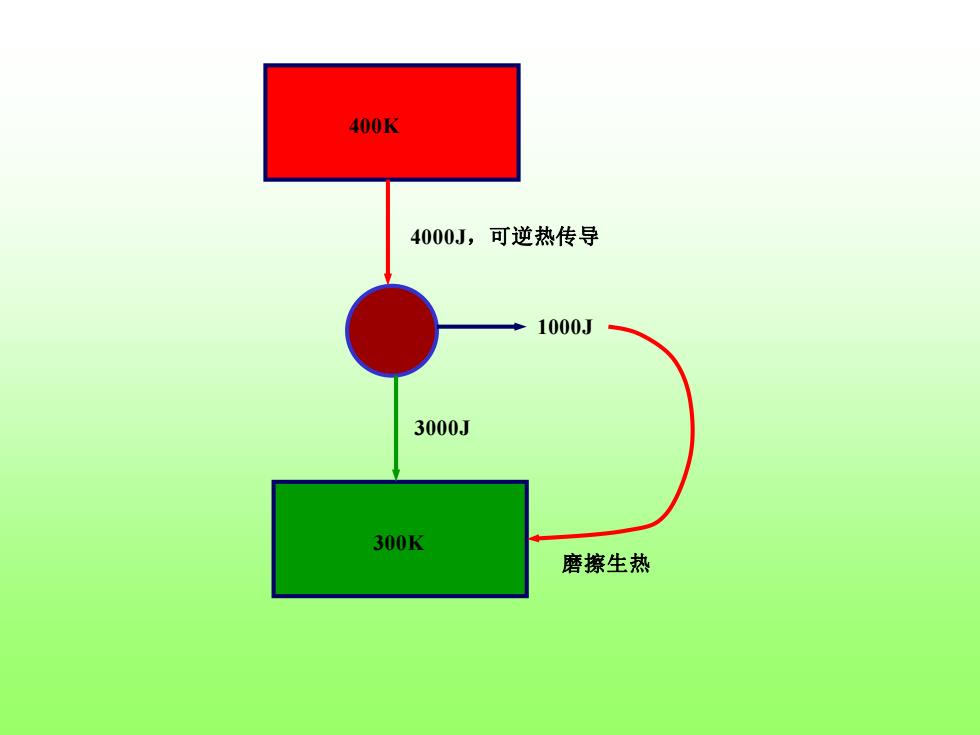
4000J,可逆热传导 3000J 1000J 磨擦生热 300K 400K

·例6.02的气态方程为:pV(1-Bp)=nRTB=-0.00094,求在 273K下,将0.5mol02从10个大气压降至1个大气压的△G? 。解:dT=0 △G=Vdp V=nRT/p(1-βp) △GnRT/p(1-βp)dp=nRT[1/p(l-Bp)ldp ● =nRT[1/p+β/(1-βpldp=nRT[dp/ptp/1-pp)dpl ● AG=nRT[In(p2/p)-In(1-Bp2)/(1-Bp1)] =0.5·8.314273[ln1/10-ln(1-βp2)/1-βp1)l =-2604J 此过程的△G=-2604J
• 例6. O2的气态方程为: pV(1-p)=nRT =-0.00094, 求在 273K下,将0.5mol O2从10个大气压降至1个大气压的G? • 解: dT=0 G=∫Vdp • V=nRT/p(1-p) • G=∫nRT/p(1-p)dp=nRT∫[1/p(1-p)]dp • =nRT∫[1/p+/(1-p)]dp=nRT[∫dp/p+∫/(1-p)dp] • G=nRT[ln(p2 /p1 )-ln(1-p2 )/(1-p1 )] • =0.5·8.314·273·[ln1/10-ln(1-p2 )/(1-p1 )] • =-2604 J • 此过程的G=-2604J

·例7.设大气的温度均匀为T,空气分子量为M,求大气压力与 高度h的关系? 解:令1摩尔空气从h处可逆地降到海平面(h=O0). ● 令在h处大气压力为p,海平面的大气压力为p: ● dT=0,体系为理想气体,理想气体等温膨胀过程的熵变为: △S体=Rln(P1/p2)=Rln(plpo) 在下降过程中,体系的重力势能全部变为热能传递给周围环境: ● △S环=-Q/T=mgh/T(环境吸热为正) 因为此过程是一可逆过程,故有: △S总=△S体+△S环=nRln(p/po)+mgh/T=0 In(p/po)=-mgh/nRT=-Mgh/RT ● p/po=exp[-Mgh/RT] p片Po'e-Mgb/RT此即为Boltzmanni高度分布律
• 例7. 设大气的温度均匀为T,空气分子量为M,求大气压力p与 高度h的关系? • 解: 令1摩尔空气从h处可逆地降到海平面(h0=0). • 令在h处大气压力为p, 海平面的大气压力为p0 . • • ∵ dT=0, 体系为理想气体, 理想气体等温膨胀过程的熵变为: • S体=Rln(p1 /p2 )=Rln(p/p0 ) • 在下降过程中,体系的重力势能全部变为热能传递给周围环境: • S环=-Q/T=mgh/T (环境吸热为正) • 因为此过程是一可逆过程,故有: • S总=S体+S环=nRln(p/p0 )+mgh/T=0 • ln(p/p0 )=-mgh/nRT=-Mgh/RT • p/p0=exp[-Mgh/RT] • p=p0·e-Mgh/RT 此即为Boltzmann高度分布律
例8. 一均匀长杆一端的温度为T1,另一端的温度为T2,求 杆的温度达到平衡后,此过程的△S,并证明△S>0? 解:如图:纵坐标为温度T,横坐标为杆的长度x.设T2>T1,在初始时刻,杆的 温度呈线性分布,故杆上任意处的初始温度为: T初=T+(T2T)L0x (1) d小 达到热平衡后,杆上处处的温度相同,均为: T末=(T1+T2)/2 求AS: T, 因为杆的初始温度是处处不相同的,而最终 温度又是处处相同的,故杆上每一点的温度 变化都不相同,故每一小段的熵变都不相同. T2-T1 (T2-TI)x/Lo 在计算整个杆的总熵变时,须对每一小段杆 长求其熵变,然后对整个杆长进行积分,其 C 积分结果才是长杆的总熵变
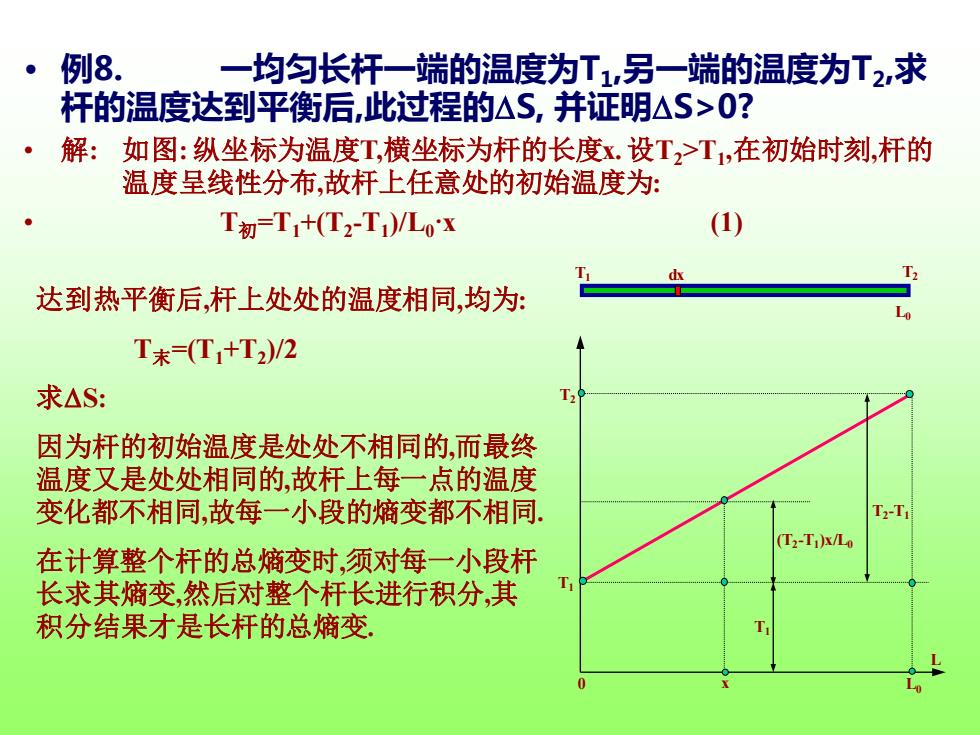
• 例8. 一均匀长杆一端的温度为T1 ,另一端的温度为T2 ,求 杆的温度达到平衡后,此过程的S, 并证明S>0? • 解: 如图: 纵坐标为温度T,横坐标为杆的长度x. 设T2>T1 ,在初始时刻,杆的 温度呈线性分布,故杆上任意处的初始温度为: • T初=T1+(T2 -T1 )/L0·x (1) T1 T2 T2 T1 L0 dx 0 x L L0 T1 T2 -T1 (T2 -T1 )x/L0 达到热平衡后,杆上处处的温度相同,均为: T末=(T1+T2 )/2 求S: 因为杆的初始温度是处处不相同的,而最终 温度又是处处相同的,故杆上每一点的温度 变化都不相同,故每一小段的熵变都不相同. 在计算整个杆的总熵变时,须对每一小段杆 长求其熵变,然后对整个杆长进行积分,其 积分结果才是长杆的总熵变