
热化学
热 化 学

第八节 热化学 热化学(hermochemistry): o 热化学是一门比较古老的学科,主 要任务是测定物质的热力学量。但 是20世纪以来热化学有很大发展,热 化学的应用领域从测定物资的热数 据扩张到化学动力学、生命科学、 农学、医学、药学等领域
第八节 热化学 • 热化学(thermochemistry): • 热化学是一门比较古老的学科,主 要任务是测定物质的热力学量。但 是20世纪以来热化学有很大发展, 热 化学的应用领域从测定物资的热数 据扩张到化学动力学、生命科学、 农学、医学、药学等领域

热化学方程式 ·热化学方程式是表示化学反应始末态之间关系的方 程,它不考虑反应实际上能否进行到底,只表示反应 前后物质的量的反应热效应之间的关系, 。 热化学反应方程式须注明参加反应物质的状态,温度, 压力和反应进行的各种条件等, ·例:石墨与氧反应生成二氧化碳的热化学方程式为: C(石墨,1p)+02(g,lp (298K,1pC02(g1p △Hm(298K)=-393.5kJ.mo1
• 一 热化学方程式 • 热化学方程式是表示化学反应始末态之间关系的方 程, 它不考虑反应实际上能否进行到底, 只表示反应 前后物质的量的反应热效应之间的关系. • 热化学反应方程式须注明参加反应物质的状态, 温度, 压力和反应进行的各种条件等. • 例: 石墨与氧反应生成二氧化碳的热化学方程式为: C +O2 CO2 rHm(298K)=-393.5 kJ.mol-1 (石墨,1p0 ) (g,1p0 ) (g,1p0 ) (298K, 1p0 )

二 Hess定律(Hess'sLaW) ·1840年,盖斯从大量实脸数据中总结出著名的Hss定律. ·Hss定律:化学反应的热效应只与反应的始态和末态有关,与 反应的具体途径无关.也称热效应总值一定定律. ·盖斯定律的使用不是无条件的,只有满足一定条件才能使用. 其条件为:需规定反应进行的环境条件. ·等容反应: Q=△U ·等压反应: Qp△H ·上式将本来是过程量的热效应与体系的状态函数△U或△H联 系起来,而后者是与途径无关的,故在规定了反应的进行条件 (等容或等压)时,反应的过程量Q也可能具有某种状态函数的 性质. ·注意:应用盖斯定律时,反应不能有有用功,知电功等
二 Hess定律(Hess’s Law) • 1840年, 盖斯从大量实验数据中总结出著名的Hess定律. • Hess定律: 化学反应的热效应只与反应的始态和末态有关, 与 反应的具体途径无关. 也称热效应总值一定定律. • 盖斯定律的使用不是无条件的, 只有满足一定条件才能使用. 其条件为: 需规定反应进行的环境条件. • 等容反应: QV =rU • 等压反应: Qp =rH • 上式将本来是过程量的热效应与体系的状态函数rU或rH联 系起来, 而后者是与途径无关的, 故在规定了反应的进行条件 (等容或等压)时, 反应的过程量Q也可能具有某种状态函数的 性质. • 注意: 应用盖斯定律时, 反应不能有有用功, 如电功等

·用盖斯定律可以求算许多难以直接测定 的化学反应的热效应. ·例1.求下列化学反应的热效应,即反应的△H? 2C(石墨)+3H2(g,1p) 298K→ C2H6(g,1p) 已知如下反应在298K下的热效应: ·(1)C(石墨)+02(g,1p)→C02(g,1p) △H=-393.15kJ.mo1 ·(2)H2(g,1p)+0.502(g,1p)→H200) △H=-286.0kJ.mo1 ·(3)CzH6g,1pt3.502(g,1p)→C02(g,1p)+3H200 △H=-1560.0kJ.mo1
• 用盖斯定律可以求算许多难以直接测定 的化学反应的热效应. • 例1. 求下列化学反应的热效应,即反应的H? • 2C(石墨)+3H2 (g,1p0 ) C2H6 (g,1p0 ) • 已知如下反应在298K下的热效应: • (1) C(石墨)+O2 (g,1p0 ) →CO2 (g,1p0 ) H=﹣393.15 kJ.mol-1 • (2) H2 (g,1p0 )+0.5O2 (g,1p0 ) →H2O(l) H=﹣286.0 kJ.mol-1 • (3) C2H6 (g,1p0 )+3.5O2 (g,1p0 ) → CO2 (g,1p0 ) +3H2O(l) H=﹣1560.0 kJ.mol-1 298K

·解:题给反应可以由已知条件中所列的三个反应组 合得到,反应的总热效应便可由此三个反应的热效 应求出 。 将)×2+(2)×3一3)即得题给的反应,故有: △H=△H1×2+△H2×3-△H3 ● =2×(-393.15)+3×(-286)-(-1560) ● =一85kJ.mo1 ·实际上,由石墨和氢气直接化合生成乙烷是非常 因难的,用量热的手段直接测定此反应的热效应 几乎是不可能的,但是,用热化学方法,利用盖 斯定律,可以由其它较容易获得的反应热效应求 出
• 解: 题给反应可以由已知条件中所列的三个反应组 合得到, 反应的总热效应便可由此三个反应的热效 应求出. • 将(1)×2+(2)×3-(3)即得题给的反应,故有: • rH=rH1×2+ rH2×3- rH3 • =2×(-393.15)+3×(-286)-(-1560) • =-85kJ.mol-1 • 实际上,由石墨和氢气直接化合生成乙烷是非常 困难的,用量热的手段直接测定此反应的热效应 几乎是不可能的,但是,用热化学方法,利用盖 斯定律,可以由其它较容易获得的反应热效应求 出

三 反应热效应的计算 ·1.生成焓(enthalpy of formation): ·1p下,由最稳定的单质化合生成1p下的1mol 纯化合物的反应焓变,称为此物质的标准摩尔 生成焓.记为: △Hm0 ·处于标准状态的稳定单质的生成焓等于零: △Hm(稳定单质)=0 。标准状态:温度为T,压力为1p
三 反应热效应的计算 • 1. 生成焓(enthalpy of formation): • 1p0下, 由最稳定的单质化合生成1p0下的1mol 纯化合物的反应焓变, 称为此物质的标准摩尔 生成焓. 记为: • fHm 0 • 处于标准状态的稳定单质的生成焓等于零: • fHm 0 (稳定单质)=0 • 标准状态: 温度为T, 压力为1p0

·如: ·0.5H2(g,1pt0.5Cl2(g,1p) 298K.HCl(g,1p) 测得:△Hn0=-92.31kJ.mo1 ,因为此反应即为HC的生成反应,所以,此 反应的焓变即为HC的生成焓,因反应在标准 条件下进行,故所得反应焓即为标准摩尔生 成焓。 A Hm(HCI,g,298K)=-92.31 kJ.mol-1
• 如: • 0.5H2 (g,1p0 )+ 0.5Cl2 (g,1p0 ) HCl(g,1p0 ) • 测得: rHm 0=-92.31kJ.mol-1 • 因为此反应即为HCl的生成反应,所以,此 反应的焓变即为HCl的生成焓,因反应在标准 条件下进行,故所得反应焓即为标准摩尔生 成焓。 fHm 0 (HCl,g,298K)=-92.31 kJ.mol-1 298K
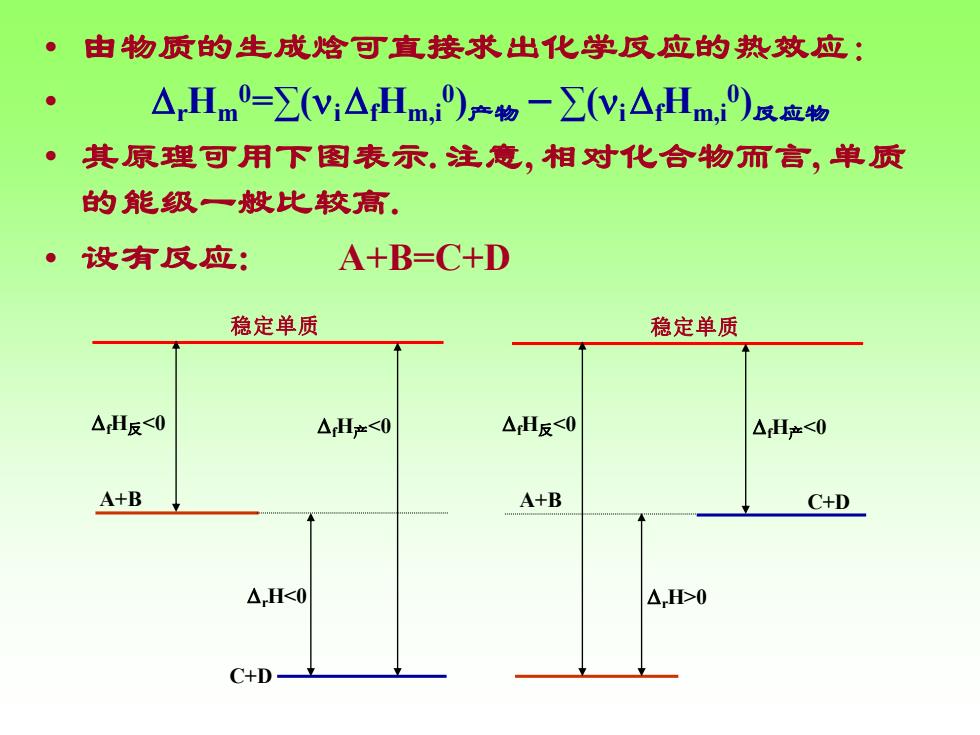
。由物质的生成焓可直接求出化学反应的热效应: △Hm0=∑(yi△Hm,)产物一∑(y:△Hm)a应物 ·其原理可用下图表示.注意,相对化合物而言,单质 的能级一般比较高. 设有反应: A+B=C+D 稳定单质 稳定单质 △H反<0 △H产<0 △H反<0 △H产<0 A+B A+B C+D △H<0 △H0 C+D-
• 由物质的生成焓可直接求出化学反应的热效应: • rHm 0=∑(i fHm,i 0 )产物-∑(i fHm,i 0 )反应物 • 其原理可用下图表示. 注意, 相对化合物而言, 单质 的能级一般比较高. • 设有反应: A+B=C+D 稳定单质 A+B C+D fH反0

·2.燃烧焓(combustion enthalpy): ·1moI纯化合物在1p下完全燃烧所放出的热量,称为 该化合物的燃烧焓,记为: △,Hm0 燃烧焓一般适用于有机化合物,规定燃烧后的产物是: ● C→C02(气态) H→H,0(液态) S-→S02(气态) N→N2(气态) ● C→HCI (aq) Br→HBr(aq) ·若燃烧后的产物不是上述产物,在计算物质的燃烧焓 时,需对测定结果进行校正.如有机化合物燃烧后,C 不一定完全燃烧,可能由未燃烧的碳黑,N也可能生成 NO,等,在进行物质的燃烧焓测定时,对这些误差必须 进行校正
• 2. 燃烧焓(combustion enthalpy): • 1mol纯化合物在1p0下完全燃烧所放出的热量, 称为 该化合物的燃烧焓, 记为: • cHm 0 • 燃烧焓一般适用于有机化合物, 规定燃烧后的产物是: • C→CO2 (气态) H→H2O (液态) • S→SO2 (气态) N→N2 (气态) • Cl→HCl (aq) Br→HBr (aq) • 若燃烧后的产物不是上述产物, 在计算物质的燃烧焓 时, 需对测定 结果进行校正. 如有机化合物燃烧后, C 不一定完全燃烧,可能由未燃烧的碳黑, N也可能生成 NO2等, 在进行物质的燃烧焓测定时,对这些误差必须 进行校正