
热力学第一定律 习题辅导
热力学第一定律 习题辅导

·体积功的主要计算公式: W=-Jp外dV 功的通用计算公式 ·1.理想气体等温可逆过程: W=jw-兴'wRT
• 体积功的主要计算公式: W=-p外dV 功的通用计算公式 • 1. 理想气体等温可逆过程: 2 1 V 1 V 2 nRT V W pdV dV nRTln V V = − = − =

2.等外压过程: W=-∫PdV=-p外∫dV=-P外(V,-V) 理想气体外压恒等于体系末态压力的 等温过程: W=-p2(V2-V)=-nRT,+p2 nRT=nRT(Pz-1) 3.自由膨胀过程: P外=0, 有:W=0
3. 自由膨胀过程: p外=0, 有: W=0 2. 等外压过程: W p dV p dV p (V V ) = − = − = − − 外 外 外 2 1 理想气体外压恒等于体系末态压力的 等温过程: 1 2 2 2 1 2 2 1 1 nRT p W p (V V ) nRT p nRT( 1) p p = − − = − + = −
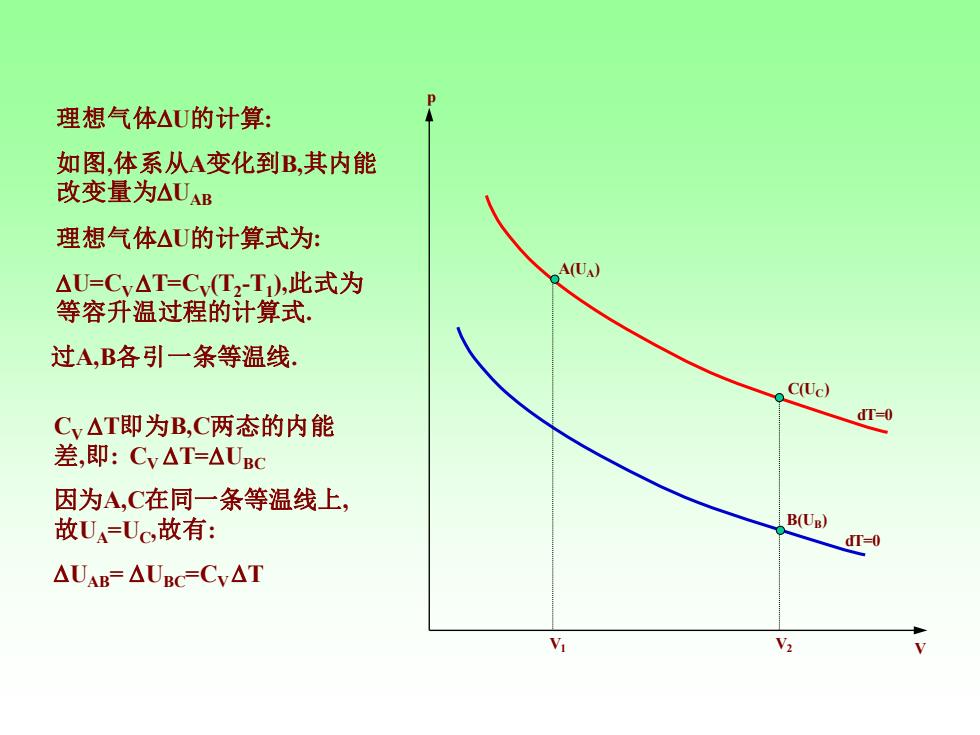
理想气体△U的计算: 如图,体系从A变化到B,其内能 改变量为△UAB 理想气体△U的计算式为: △U=Cy△T=Cv(T2-T),此式为 A(UA) 等容升温过程的计算式: 过A,B各引一条等温线, C(Uc) Cy△T即为B,C两态的内能 dT-0 差,即:Cy△T=△UBC 因为A,C在同一条等温线上, 故U=Uc,故有: B(Ug) dT=0 △UAB=△UBC=Cv△T
p V dT=0 dT=0 C(U C) V 1 V2 A(UA) B(UB) 理想气体 U的计算 : 如图 ,体系从 A变化到B,其内能 改变量为 UAB 理想气体 U的计算式为 : U=CV T=C V(T 2 - T 1 ),此式为 等容升温过程的计算式. 过A,B各引一条等温线. CV T即为B,C两态的内能 差,即: CV T=UBC 因为A,C在同一条等温线上 , 故 U A=U C ,故有 : UAB= UBC=CV T
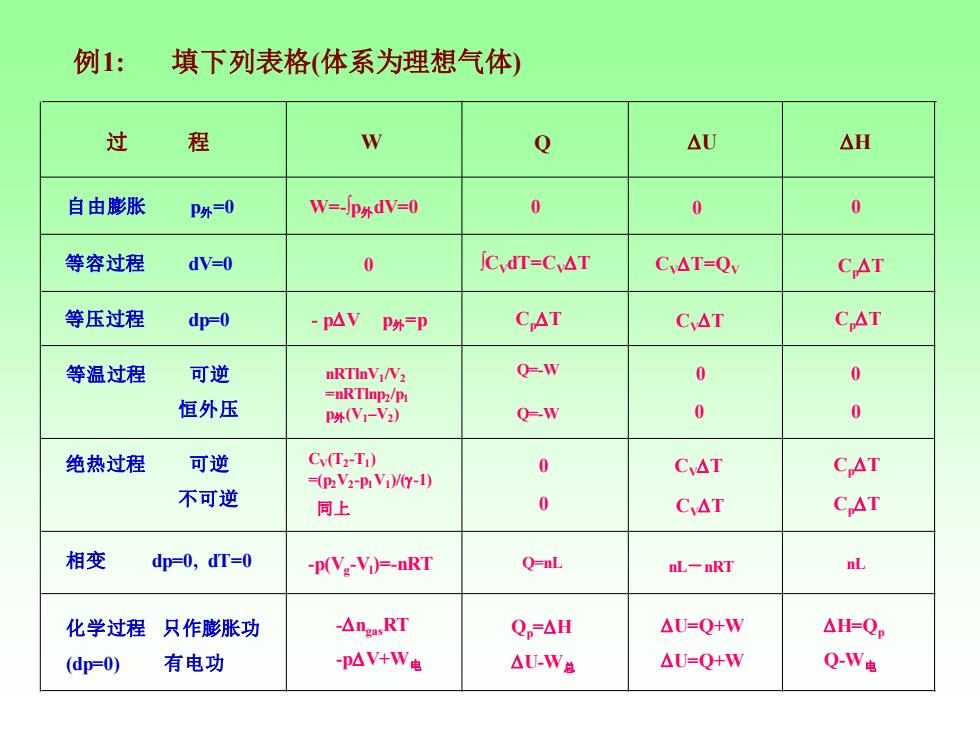
例1: 填下列表格(体系为理想气体) 过 程 Q △U △H 自由膨胀 P外=0 W=-p外dV=0 0 0 0 等容过程 dV=0 0 jCdT=Cv△T CyAT=Qv CAT 等压过程 dp=0 -pAV P外=P CAT CAT CAT 等温过程 可逆 nRTInVNV2 Q-W 0 0 恒外压 =nRTInp2/p P(N1-V2) Q-W 0 0 绝热过程 可逆 Cy(Tz-T1) 0 CyAT =(pz V2-Pr Vi)(Y-1) CAT 不可逆 同上 0 CAT CAT 相变 dp=0,dT=0 -p(V:-Vi)=-nRT Q=nL nL-nRT nL 化学过程只作膨胀功 -△ngasRT Qp=AH △U-Q+W △H=Qp (dp=0) 有电功 -pAV+W电 △U-W总 △U=Q+W QW电
例1: 填下列表格(体系为理想气体) 过 程 W Q U H 自由膨胀 p外=0 等容过程 dV=0 等压过程 dp=0 等温过程 可逆 恒外压 绝热过程 可逆 不可逆 相变 dp=0, dT=0 化学过程 只作膨胀功 (dp=0) 有电功 nRTlnV1 /V2 =nRTlnp2 /p1 p外(V1–V2 ) W=-∫p外dV=0 0 0 0 0 0 0 0 0 0 0 ∫CVdT=CVT CVT=QV CpT - pV p外=p CpT CVT CpT Q=-W Q=-W CV(T2 -T1 ) =(p2V2 -p1V1 )/(-1) 同上 CVT CVT CpT CpT -p(Vg -Vl )=-nRT Q=nL nL-nRT nL -ngasRT -pV+W电 Qp=H U-W总 U=Q+W U=Q+W H=Qp Q-W电
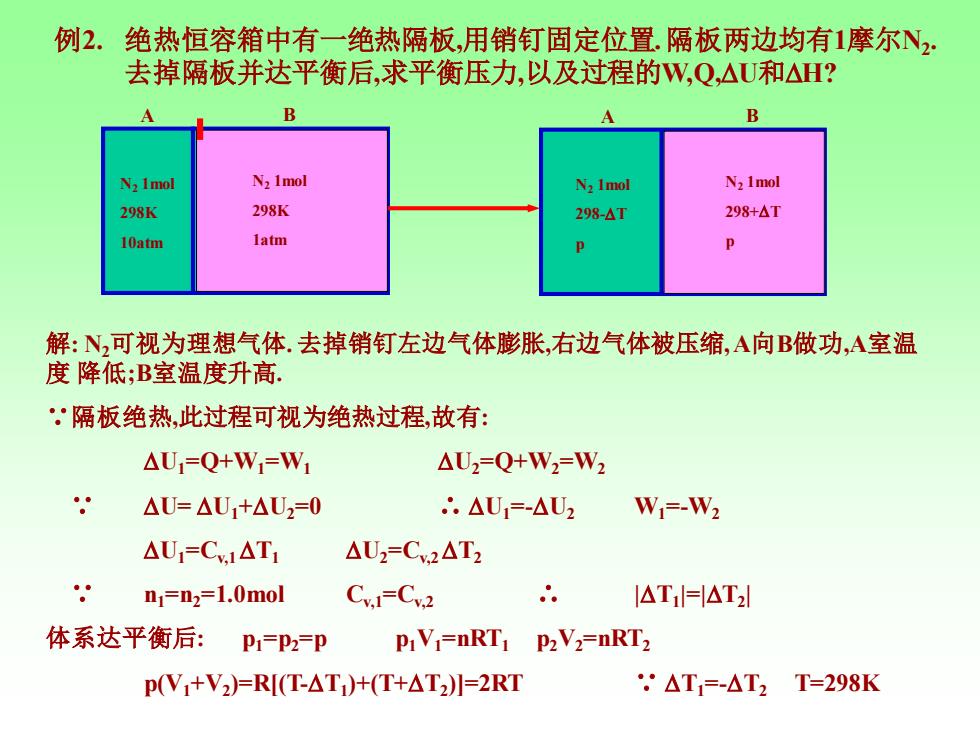
例2.绝热恒容箱中有一绝热隔板,用销钉固定位置.隔板两边均有1摩尔N2, 去掉隔板并达平衡后,求平衡压力,以及过程的W,Q,△U和△H? B N2 Imol N2 1mol N2 Imol N2 1mol 298K 298K 298-△1 298+△T 10atm latm 解:N2可视为理想气体.去掉销钉左边气体膨胀,右边气体被压缩,A向B做功,A室温 度降低;B室温度升高. 隔板绝热,此过程可视为绝热过程,故有: △U1=Q+W=W △U2=Q+W2=W2 △U=△U1+△U2=0 .△U1=-△U2 W=-W2 △U1=C,1△T1 △U2=C2△T2 nj=n2=1.0mol CyI=Cv2 I△T=AT2 体系达平衡后: PI=P2=P PiVi=nRT1 P2V2=nRT2 pV+V2=R[(T-△T)H(T+△T2=2RT .△T=-△T2T=298K
例2. 绝热恒容箱中有一绝热隔板,用销钉固定位置. 隔板两边均有1摩尔N2 . 去掉隔板并达平衡后,求平衡压力,以及过程的W,Q,U和H? 解: N2可视为理想气体. 去掉销钉左边气体膨胀,右边气体被压缩, A向B做功,A室温 度 降低;B室温度升高. ∵隔板绝热,此过程可视为绝热过程,故有: U1=Q+W1=W1 U2=Q+W2=W2 ∵ U= U1+U2=0 ∴ U1=-U2 W1=-W2 U1=Cv,1 T1 U2=Cv,2 T2 ∵ n1=n2=1.0mol Cv,1=Cv,2 ∴ |T1 |=|T2 | 体系达平衡后: p1=p2=p p1V1=nRT1 p2V2=nRT2 p(V1+V2 )=R[(T-T1 )+(T+T2 )]=2RT ∵ T1=-T2 T=298K N2 1mol 298K 10atm N2 1mol 298K 1atm A B N2 1mol 298-T p N2 1mol 298+T p A B

pV=2RT (V+V2=V) 始态:p1V'=RTV'=RTp';p2'V2=RTV2'=RTp2 V'+V2'=RT/p1'+RTp2'=RT1/p1'+1/p2')=V p=2RT/V =2RT/IRT(1/p1'+1/p2')] =2/(1/p1'+1/p2) =2/1/10+1)=1.82atm 整个体系为一孤立体系,故有: △U=0 △H=0 Q=0 此体系最终的压力为一定值,但是体系的最终温度为一不定值, 其具体数值取决于膨胀过程的可逆程度
pV=2RT (V1+V2=V) 始态: p1 ’V1 ’=RT V1 ’=RT/p1 ’; p2 ’V2 ’=RT V2 ’=RT/p2 ’ V1 ’+V2 ’=RT/p1 ’+RT/p2 ’=RT(1/p1 ’+1/p2 ’)=V p=2RT/V =2RT/[RT(1/p1 ’+1/p2 ’)] =2/(1/p1 ’+1/p2 ’) =2/(1/10+1)=1.82 atm 整个体系为一孤立体系,故有: U=0 H=0 Q=0 此体系最终的压力为一定值,但是体系的最终温度为一不定值, 其具体数值取决于膨胀过程的可逆程度
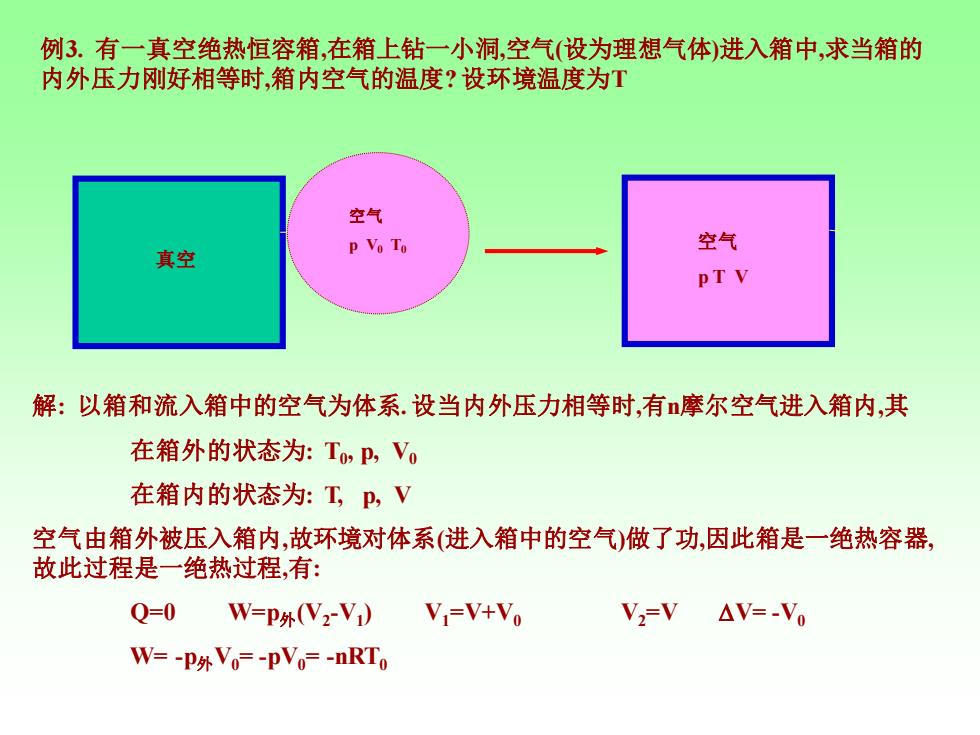
例3.有一真空绝热恒容箱,在箱上钻一小洞,空气(设为理想气体)进入箱中,求当箱的 内外压力刚好相等时,箱内空气的温度?设环境温度为T 空气 P Vo To 空气 真空 PTV 解:以箱和流入箱中的空气为体系.设当内外压力相等时,有摩尔空气进入箱内,其 在箱外的状态为:TP,Vo 在箱内的状态为:工,P,V 空气由箱外被压入箱内,故环境对体系(进入箱中的空气)做了功,因此箱是一绝热容器, 故此过程是一绝热过程,有: Q=0 W=P外(V2V) V =V+Vo V2=V△V=-Vo W=-P外Vo=-pVo=-nRTo
例3. 有一真空绝热恒容箱,在箱上钻一小洞,空气(设为理想气体)进入箱中,求当箱的 内外压力刚好相等时,箱内空气的温度? 设环境温度为T 真空 空气 p V0 T0 空气 p T V 解: 以箱和流入箱中的空气为体系. 设当内外压力相等时,有n摩尔空气进入箱内,其 在箱外的状态为: T0 , p, V0 在箱内的状态为: T, p, V 空气由箱外被压入箱内,故环境对体系(进入箱中的空气)做了功,因此箱是一绝热容器, 故此过程是一绝热过程,有: Q=0 W=p外(V2 -V1 ) V1=V+V0 V2=V V= -V0 W= -p外V0= -pV0= -nRT0

·因为此过程为一绝热过程,故有: △U=-W=nRTo=Cv(T-To) nRTo/Cy=T-To ● T=To+nRTo/Cy=To(1+nR/Cy) ● T=To(1+(Cp-Cy)/Cy) Cp-Cy=nR T=To(1+Y-1)=YTo ·箱中空气的温度为T=YT ·如:To=298K ● 体系为单原子分子理想气体,Y=53 ● T=5/3×298=497K
• 因为此过程为一绝热过程,故有: • U=-W=nRT0=CV(T-T0 ) • nRT0 /CV=T-T0 • T=T0+nRT0 /CV=T0 (1+nR/CV) • T=T0 (1+(Cp -CV)/CV) ∵ Cp -CV=nR • T=T0 (1+-1)=T0 • 箱中空气的温度为T=T0 . • 如: T0=298K • 体系为单原子分子理想气体, =5/3 • T=5/3×298=497K

·例4.对一种单原子分子理想气体沿某一可逆途径加热,其热容 C=R,求此路径的性质? 。解:设有1摩尔理想气体,Cv=3/2R ● δQ=dU-δW=CvdT+pdV=CvdT+RT/VdV δQ/dT=Cv+(RTW)dV/dT 'δQ/dT=C=R(题给条件) Cv+RT/V(dV/dT)=R=3/2R+RT/V(dV/dT) ● -1/2R=RT/V(dV/dT)-1/2=TdlnV/dT -1/2dT/T=-1/2dInT=dlnV 积分: ● dIn V=-1/2dInT ● In V=-1/2InT+K' InV+InT12=K' ● In(VTIR)=K' VTIR=K 。 当气体沿VT2=常数的路径加热时,此路径的热容C=R
• 例4.对一种单原子分子理想气体沿某一可逆途径加热, 其热容 C=R,求此路径的性质? • 解: 设有1摩尔理想气体, CV=3/2R • Q=dU-W=CVdT+pdV=CVdT+RT/VdV • Q/dT=CV+(RT/V)dV/dT • ∵ Q/dT=C=R (题给条件) • ∴ CV+RT/V(dV/dT)=R=3/2R+RT/V(dV/dT) • -1/2R=RT/V(dV/dT) -1/2=TdlnV/dT • -1/2dT/T=-1/2dlnT=dlnV • 积分: • ∫dlnV=-1/2∫dlnT • lnV=-1/2lnT+K’ lnV+lnT1/2=K’ • ln(VT1/2)=K’ • VT1/2=K • 当气体沿VT1/2=常数的路径加热时, 此路径的热容C=R