
双液系相图
双液系相图

两组分相图 ·两组分体系的相律可表达为: K=2;Φ=2 f=4一Φ (10 f=0, Φmax=4,最多四相共存. ·Φ=,fmax3,需三维图象才能完整描绘体系状态 ·二元体系的相图常常固定某因素不变(如温度或压 力),用二维平面相图表示体系状态的变化情况. ·二元体系的相图常为: T一x图;p一x图
两组分相图 • 两组分体系的相律可表达为: • K=2; =2 • f=4- (1) • f=0, max=4, 最多四相共存. • =, fmax=3, 需三维图象才能完整描绘体系状态. • 二元体系的相图常常固定某因素不变(如温度或压 力),用二维平面相图表示体系状态的变化情况. • 二元体系的相图常为: • T-x图; p-x图

第三节 双液条相图 liqiud-liqiud phase diagram ·物质一般具有气一液一固三种形态,相 图中也应该反映物质气相、液相、固相 间的关条和相互的变化。 ·双液条相图描述的是两组分体条气、液 相态与浓度、温度和压力之间的关系。 ·故双液系相图只是两组分相图中的一部 分,描述了温度较高区域的相变化
第三节 双液系相图 liqiud-liqiud phase diagram • 物质一般具有气-液-固三种形态,相 图中也应该反映物质气相、液相、固相 间的关系和相互的变化。 • 双液系相图描述的是两组分体系气、液 相态与浓度、温度和压力之间的关系。 • 故双液系相图只是两组分相图中的一部 分,描述了温度较高区域的相变化

一。 phase diagram of ideal solution: ·理想溶液各组分在全部浓度范围内均遵守拉 乌尔定律,只要掌握了A,B的饱和蒸汽压数据, 其相图可以计算出来 p一x图: PA=PAXA PB=PBXB=PB·(1-XA) ● P=PA+PB =PAXA+PB"(1-XA) 。体系的总压为: P=PB+(PA一PB)XA (2)
一 . phase diagram of ideal solution: • 理想溶液各组分在全部浓度范围内均遵守拉 乌尔定律,只要掌握了A,B的饱和蒸汽压数据, 其相图可以计算出来. • p-x图: • pA= pA * xA • pB= pB * xB= pB * (1-xA) • p = pA+ pB • = pA * xA + pB * (1-xA) • 体系的总压为: • p = pB *+(pA *-pB * )xA (2)
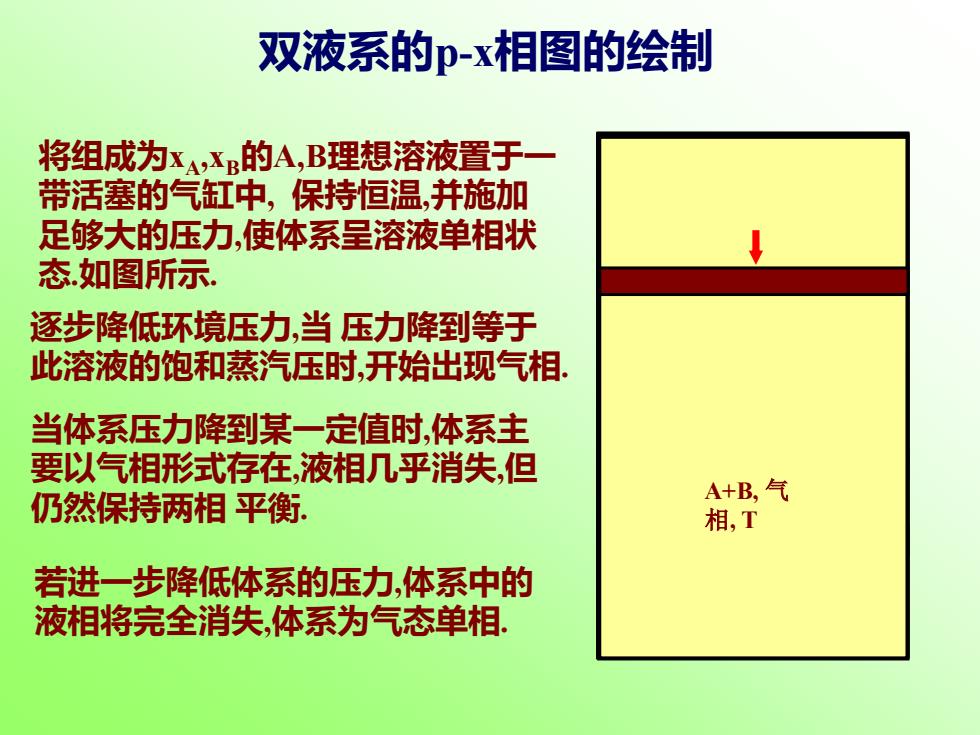
双液系的p-x相图的绘制 将组成为XA,XB的A,B理想溶液置于一 带活塞的气缸中,保持恒温,并施加 足够大的压力,使体系呈溶液单相状 态如图所示. 逐步降低环境压力,当压力降到等于 此溶液的饱和蒸汽压时,开始出现气相. 当体系压力降到某一定值时,体系主 要以气相形式存在,液相几乎消失,但 仍然保持两相平衡. A+B,气 相,T 若进一步降低体系的压力,体系中的 液相将完全消失,体系为气态单相
A+B, 溶液, T 开始出现气相, 体系达气液两相 平衡. A+B, 溶液, T A+B, 气相, T A+B, 溶液, T A+B, 气相, T A+B, 溶液, T A+B, 气相, T A+B, 气 相, T 将组成为xA,xB的A,B理想溶液置于一 带活塞的气缸中, 保持恒温,并施加 足够大的压力,使体系呈溶液单相状 态.如图所示. 逐步降低环境压力,当 压力降到等于 此溶液的饱和蒸汽压时,开始出现气相. 当体系压力降到某一定值时,体系主 要以气相形式存在,液相几乎消失,但 仍然保持两相 平衡. 若进一步降低体系的压力,体系中的 液相将完全消失,体系为气态单相. 双液系的p-x相图的绘制
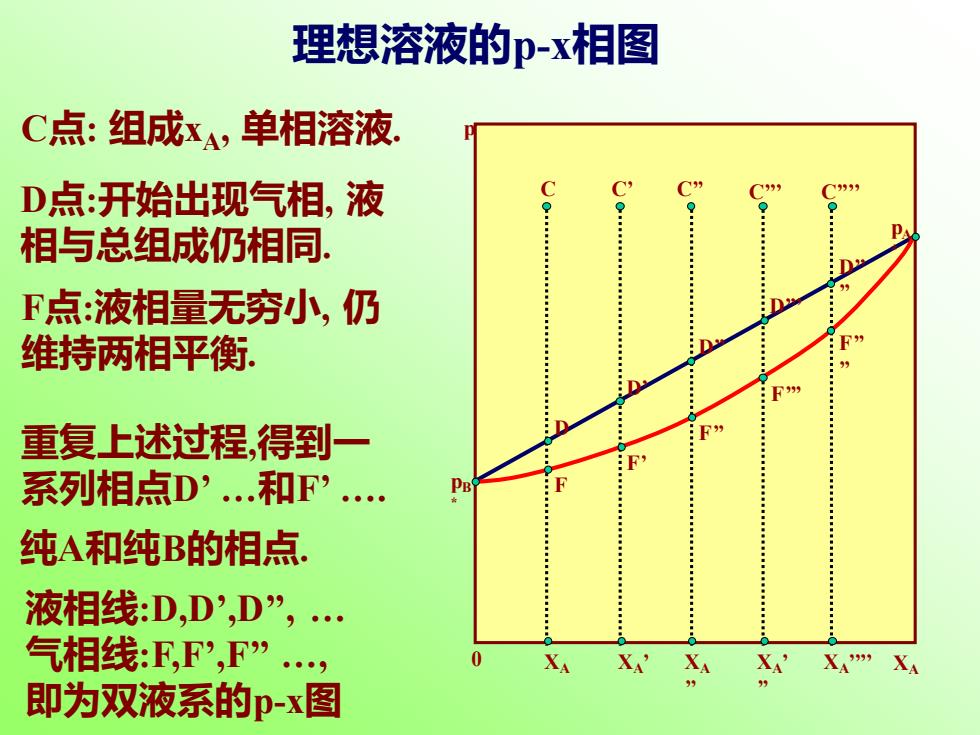
理想溶液的p-x相图 C点:组成x4,单相溶液. D点:开始出现气相,液 相与总组成仍相同. F点:液相量无穷小,仍 维持两相平衡. 重复上述过程,得到一 系列相点D’.和F?. 纯A和纯B的相点. 液相线D,D,D”, 气相线:E,F?,F” XA 即为双液系的p-x图
XA 0 p pB * pA * D F C XA D’ F’ C’ XA ’ D’’ F’’ C’’ XA ’’ C’’’ D’’’ F’’’ XA ’ ’’ C’’’’ D’’ ’’ F’’ ’’ XA ’’’’ 理想溶液的p-x相图 C点: 组成xA, 单相溶液. D点:开始出现气相, 液 相与总组成仍相同. F点:液相量无穷小, 仍 维持两相平衡. 重复上述过程,得到一 系列相点D’ .和F’ . 纯A和纯B的相点. 液相线:D,D’,D’’, . 气相线:F,F’,F’’ ., 即为双液系的p-x图
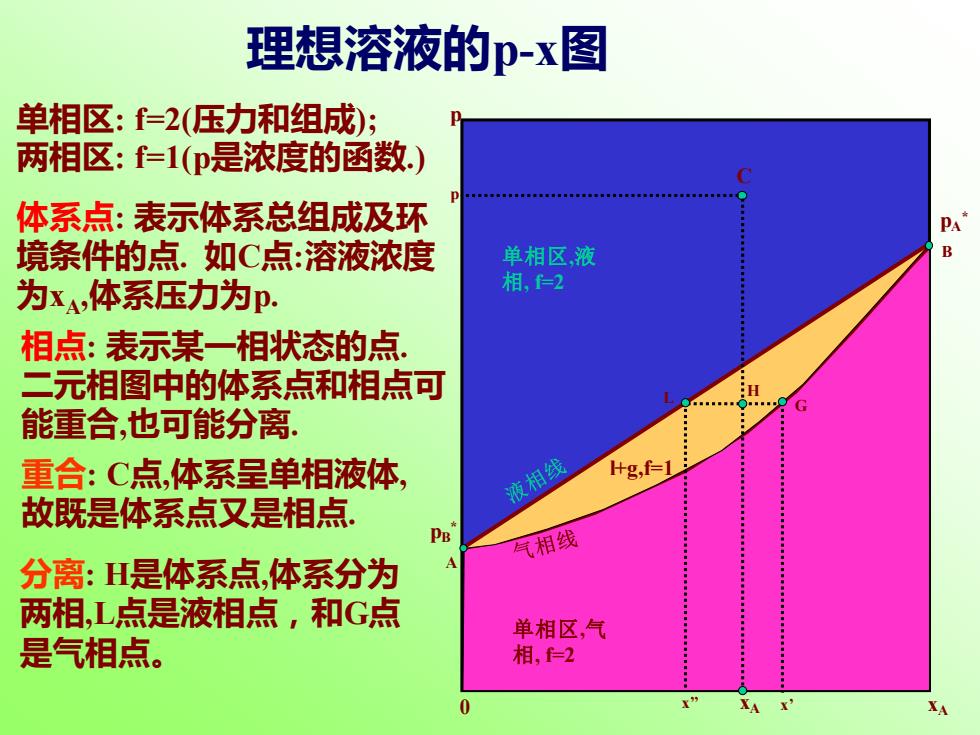
理想溶液的p-x图 单相区:f=2(压力和组成); 两相区:f=1(p是浓度的函数) 体系点:表示体系总组成及环 境条件的点.如C点:溶液浓度 单相区,液 为xA,体系压力为P. 相,2 相点:表示某一相状态的点! 二元相图中的体系点和相点可 能重合,也可能分离.。 重合:C点,体系呈单相液体, 液相线 +g,f=1 故既是体系点又是相点 气相线 分离:H是体系点,体系分为 两相,L点是液相点,和G点 单相区,气 是气相点。 相,=2 XA
0 xA p 单相区 , 气 相, f=2 单相区 , 液 相, f=2 理想溶液的 p - x 图 单相区: f=2(压力和组成); 两相区: f=1(p是浓度的函数.) 体系点: 表示体系总组成及环 境条件的点. 如 C 点 :溶液浓度 为 x A ,体系压力为p. l+g,f=1 p A * p B *A B CxA p 相点: 表示某一相状态的点. 二元相图中的体系点和相点可 能重合 ,也可能分离. 重合: C 点 ,体系呈单相液体, 故既是体系点又是相点 . 分离: H是体系点 ,体系分为 两相,L点是液相点,和 G 点 是气相点。 x’’ x’ G L H
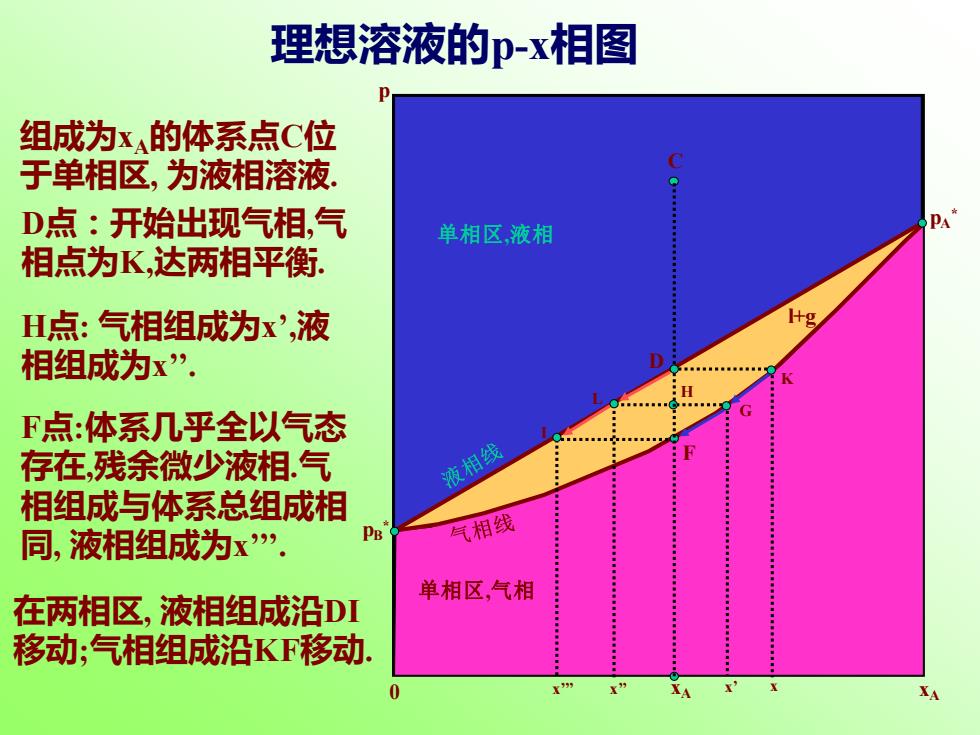
理想溶液的p-x相图 组成为x的体系点C位 于单相区,为液相溶液, D点:开始出现气相,气 单相区,液相 相点为K,达两相平衡. H点:气相组成为x',液 Hg 相组成为x”. H F点:体系几乎全以气态 存在,残余微少液相气 液相线 相组成与体系总组成相 同,液相组成为x”. PB 气相线 单相区,气相 在两相区,液相组成沿DI 移动;气相组成沿KF移动
0 xA p 单相区,液相 单相区,气相 l+g pB * pA * C xA H L G x’’ x’ F I x’’’ x D K 理想溶液的p-x相图 组成为xA的体系点C位 于单相区, 为液相溶液. D点:开始出现气相,气 相点为K,达两相平衡. H点: 气相组成为x’,液 相组成为x’’. F点:体系几乎全以气态 存在,残余微少液相.气 相组成与体系总组成相 同, 液相组成为x’’’. 在两相区, 液相组成沿DI 移动;气相组成沿KF移动
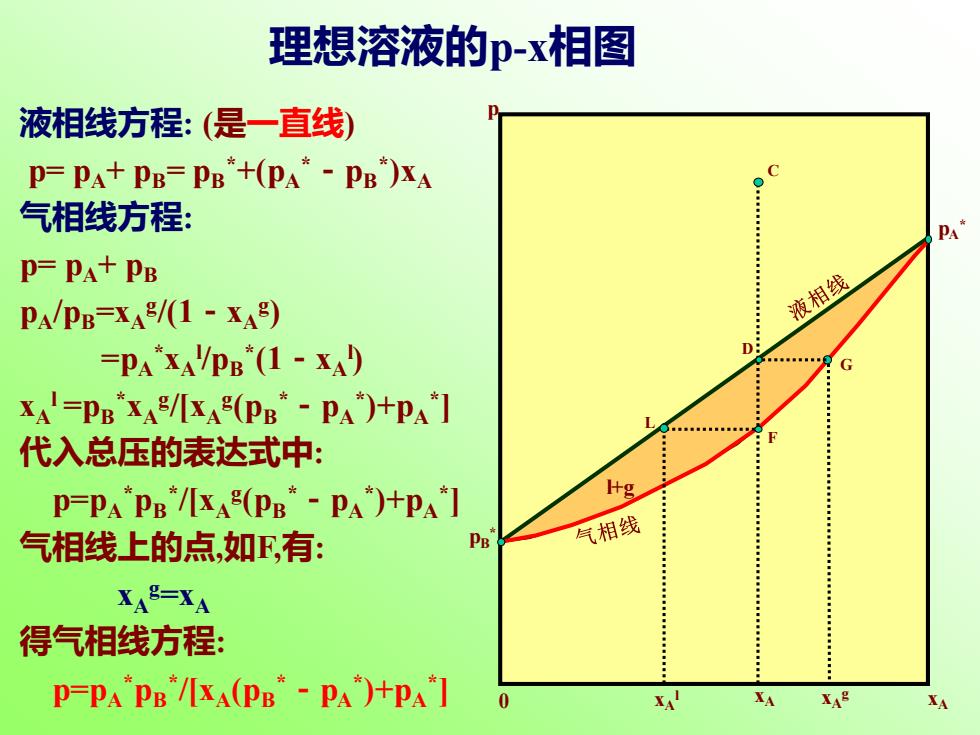
理想溶液的p-x相图 液相线方程:(是一直线) P=PA+PB=PB+(PA"-PB)xA 气相线方程: PA* P=PA+PB PA/PB=XA/(1-XA) 液相线 =PA'XA!PE(1-XA) 0 G XA=PBXA/XA(PB*-P⅓)+P⅓] 代入总压的表达式中: P=PA'PB"/[XA(PB"-PA)+PA"I 气相线上的点如F,有: 气相线 XAS-XA 得气相线方程: : P=PA PB/[XA(PB-PA)+PA"I XA XAS XA
液相线方程: (是一直线) p= pA+ pB= pB *+(pA *-pB * )xA 气相线方程: p= pA+ pB pA/pB=xA g /(1-xA g ) =pA * xA l /pB * (1-xA l ) xA l =pB * xA g /[xA g (pB *-pA * )+pA * ] 代入总压的表达式中: p=pA * pB * /[xA g (pB *-pA * )+pA * ] 气相线上的点,如F,有: xA g=xA 得气相线方程: p=pA * pB * /[xA(pB *-pA * )+pA * ] pB * pA * 0 xA p l+g xA g xA l G L xA C D F 理想溶液的p-x相图
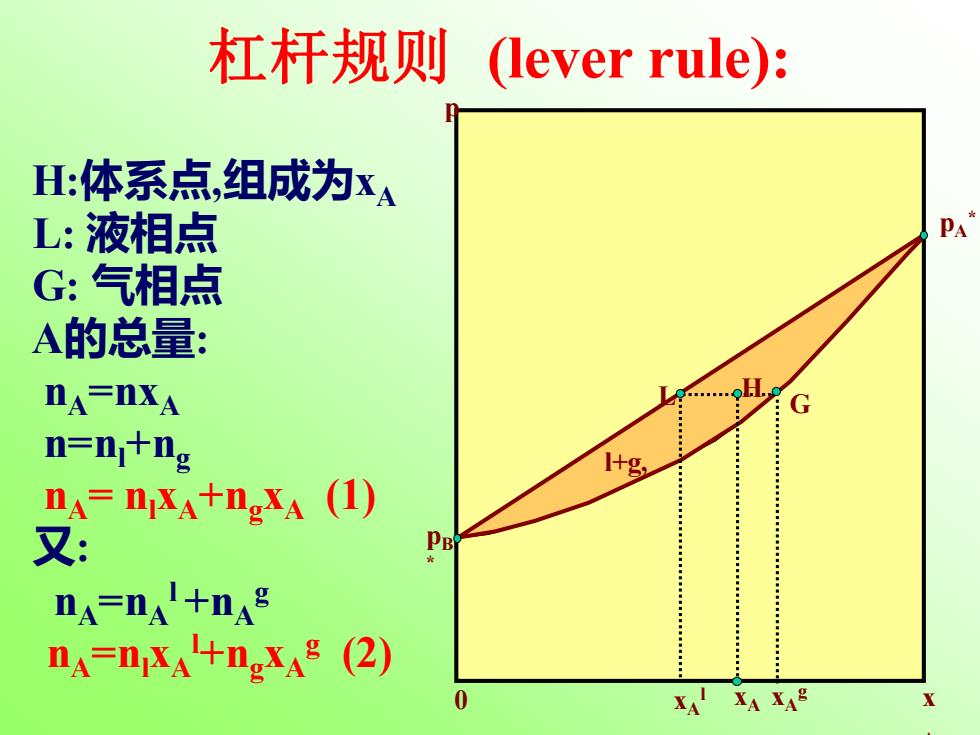
杠杆规则 (lever rule): H:体系点,组成为xA L:液相点 PA" G:气相点 A的总量: DA=DXA .且 G n=n+ng 1+g nA=nxA+ngxA (1) 又 DA=0A+0A A=nXA+nXA(2) XA XAE
pB * pA * x A 0 p l+g, L G H xA xA l xA g 杠杆规则 (lever rule): H:体系点,组成为xA L: 液相点 G: 气相点 A的总量: nA=nxA n=nl+ng nA= nlxA+ngxA (1) 又: nA=nA l +nA g nA=nlxA l+ngxA g (2)