
实际气体 节流过程
实际气体 节流过程

第七节 实际气体、节流过程 ,一、物质的状态方程(state equation) 任何纯物质的状态均可用状态方程来表示,所谓状 态方程是联系体系p-V-T三者之间关系的方程式。 ·最常见的状态方程是理想气体状态方程: pV=nRT 。 实际气体因分子之间的作用势能不能忽视,故不遵守 理想气体状态方程。对于实际气体人们从大量的实验 数据总结出几百种状态方程
第七节 实际气体、节流过程 • 一、物质的状态方程(state equation) • 任何纯物质的状态均可用状态方程来表示,所谓状 态方程是联系体系p-V-T三者之间关系的方程式。 • 最常见的状态方程是理想气体状态方程: • pV=nRT • 实际气体因分子之间的作用势能不能忽视,故不遵守 理想气体状态方程。对于实际气体人们从大量的实验 数据总结出几百种状态方程

·最著名、最常用的非理想气体的状态方程式是范 氏方程,即van der Waals equation: (p+a/Vm2)(Vm-b)=RT ·式中的a,b均为取决于物质本身性质的常数. ·aNm2:表标分子间的作用力所产生的压力,称为 内压力 b: 是对体系体积的修正,理论上,统计热力学 可以证明,b的数值等于分子体积的4倍
• 最著名、最常用的非理想气体的状态方程式是范 氏方程,即van der Waals equation: • (p+a/Vm 2 )(Vm-b)=RT • 式中的a,b均为取决于物质本身性质的常数. • a/Vm 2:表示分子间的作用力所产生的压力, 称为 内压力; • b: 是对体系体积的修正,理论上,统计热力学 可以证明, b的数值等于分子体积的4倍

·常用的状态方程还有: ·维里方程:(与热容的维里方程式相似) pV=A+B/V+C/V2+. 。贝赛罗方程: p=RT/(V-b)-a/(TV2) 、贝蒂方程: ● V=(a+B)(1-8)-A/RT 。式中: a=RT/p B=Bo(1-b/a) E=c/aT3 A=A(1-a/o)
• 常用的状态方程还有: • 维里方程: (与热容的维里方程式相似) • pVm=A+B/Vm+C/Vm 2+. • 贝赛罗方程: • p=RT/(Vm-b) -a/(TVm 2 ) • 贝蒂方程: • V=(+)(1﹣) -A/RT • 式中: • =RT/p =B0 (1﹣b/a) • =c/aT3 A=A0 (1﹣a/ )

二.节流过程 1843年Joule曾进行过气体自由膨张的实验, 并由此得出理想气体的U与体积V无关的结论. 但当时的实验是不精确的. ·1852年,Joule-Thomsoni设计了新的装置重新 测定气体的体积发生变化时,其温度随之变化 的情况.焦耳与汤姆逊设计了一种节流装置. ·这个过程可视为绝热过程.可设体系在左边是 体积为V1,经节流膨胀后,压力降为p2,体积变 为V2
二. 节流过程 • 1843年Joule曾进行过气体自由膨胀的实验, 并由此得出理想气体的U与体积V无关的结论. 但当时的实验是不精确的. • 1852年, Joule-Thomson设计了新的装置重新 测定气体的体积发生变化时, 其温度随之变化 的情况. 焦耳与汤姆逊设计了一种节流装置. • 这个过程可视为绝热过程. 可设体系在左边是 体积为V1, 经节流膨胀后, 压力降为p2, 体积变 为V2
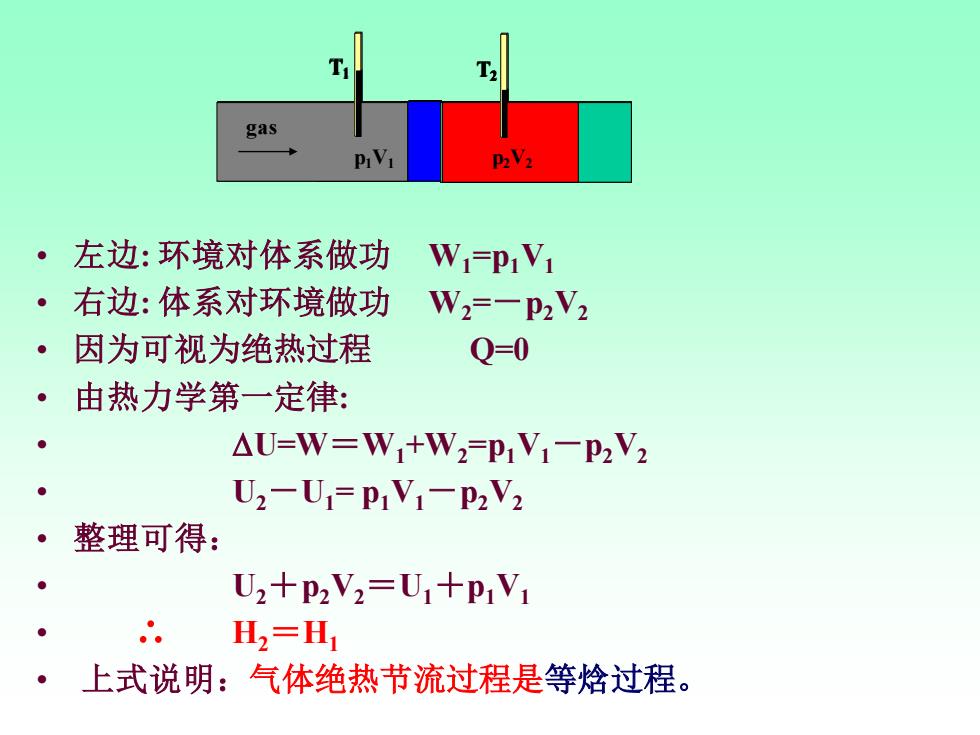
gas 。左边:环境对体系做功 W-P1V1 ·右边:体系对环境做功 W2=-P2V2 ·因为可视为绝热过程 Q=0 ·由热力学第一定律: △U=W=W+W2-pV1-P2V2 U2-U=PiV1-P2V2 整理可得: ● U2+P2V2=U1+p1V1 H,=H 上式说明:气体绝热节流过程是等焓过程
• 左边: 环境对体系做功 W1=p1V1 • 右边: 体系对环境做功 W2=-p2V2 • 因为可视为绝热过程 Q=0 • 由热力学第一定律: • U=W=W1+W2=p1V1-p2V2 • U2-U1= p1V1-p2V2 • 整理可得: • U2+p2V2=U1+p1V1 • ∴ H2=H1 • 上式说明:气体绝热节流过程是等焓过程。 gas p1V1 T1 T2 gas p1V1 T1 T2 p2V2 gas p1V1 T1 T2 p2V2 gas p1V1 T1 T2 p2V2

·气体经J一T等焓节流后,温度会发生变化: 令: -(T/op)H ·:J-T系数 4≤0 dp0 气体节流后温度升高; ● >0 dp<0 dT<0 气体节流后温度降低; ● 4=0 气体节流后温度不变 ·大多数气体的u在常温下大于零,故节流后温度 降低
• 气体经J-T等焓节流后,温度会发生变化: • 令: =(T/p)H • : J-T系数 • 0 气体节流后温度升高; • >0 dp<0 dT<0 气体节流后温度降低; • =0 气体节流后温度不变. • 大多数气体的在常温下大于零, 故节流后温度 降低

。利用J-T效应,可以使液化. ·氢气曾被认为是不可液化的气体,因为在常温下,氢 气经节流膨胀后,温度不但不降低,反而升高.这是因 为氢气的J-T系数在常温下小于零的缘故.当将氢气温 度降至195K以下时,氢气的u才变为正值,在此温度之 下,对氢气进行节流膨胀,氢气才会液化. ·气体的J-T系数是温度的函数.在某一特定温度值下, 气体的J-T系数等于零:μ=0,此时所对应的温度称为: 转化温度(inversion temperature) ·气体在转化温度下进行节流膨胀,气温不会发生变化
• 利用J-T效应, 可以使液化. • 氢气曾被认为是不可液化的气体, 因为在常温下, 氢 气经节流膨胀后, 温度不但不降低, 反而升高. 这是因 为氢气的J-T系数在常温下小于零的缘故.当将氢气温 度降至195K以下时, 氢气的才变为正值, 在此温度之 下,对氢气进行节流膨胀, 氢气才会液化. • 气体的J-T系数是温度的函数. 在某一特定温度值下, 气体的J-T系数等于零: =0,此时所对应的温度称为: • 转化温度(inversion temperature) • 气体在转化温度下进行节流膨胀, 气温不会发生变化

·对J-T系数μ的分析: ·J-T节流膨胀是一等焓过程,dH=0,故: dH=H/T)dT+H/p)Tdp=0 ● (H/T)d如y-(H/p)p (dH=0) 整理: ● u=(aT/op)=-(oH/op)/(oH/OT)p ● =-1/Cpl((U+pV)/op]T (oH/aT)=C =-1/Cpl(oU/op)T+((pV)/op]T
• 对J-T系数的分析: • J-T节流膨胀是一等焓过程, dH=0, 故: • dH=(H/T)pdT+ (H/p)Tdp=0 • (H/T)pdT=- (H/p)Tdp (dH=0) • 整理: • =(T/p)H= - (H/p)T / (H/T)p • =-1/Cp [((U+pV)/p]T ∵(H/T)p=Cp • = -1/Cp [(U/p)T+((pV)/p]T

。A.理想气体: (oU/p)=0 ((pv)/oplT-0 =-1/Cpl(oU/op)T+((pV)/op]T=0 ·理想气体:=0, 节流膨胀后温度不变
• A. 理想气体: • (U/p)T=0 ((pV)/p]T=0 • = -1/Cp [(U/p)T+((pV)/p]T =0 • 理想气体: =0, 节流膨胀后温度不变