
三组分相图
三组分相图

第六节 三组分相图 。三组分体系的相律为: f=3-Φ+2=5-Φ (1) ·要完全地描述三元体系,需要4个独立变量, 要用4维空间才能完全描述,这在现实世界 是无法做到的 f=0, Φmax-5, ·三元体条最多可以有5相共存
第六节 三组分相图 • 三组分体系的相律为: • f = 3-+2 = 5- (1) • 要完全地描述三元体系,需要4个独立变量, 要用4维空间才能完全描述,这在现实世界 是无法做到的. • f=0, max=5, • 三元体系最多可以有5相共存

·一般的三元相图,固定体系的温度和压 力,考察体系组成变化时,相图变化情况。 。此时,体系最大自由度=2,用平面图就 可描绘相的变化. ·对于疑聚体系,压力的影响很小,一般可 忽略不计. ·但温度的影响是相当大的.为了表示温度 对三元体系相图的影响,可用投影的方法, 绘制不同温度下体系的相图.也可借助于 3维动画的技术,绘制三维立体相图
• 一般的三元相图, 固定体系的温度和压 力,考察体系组成变化时,相图变化情况. • 此时, 体系最大自由度f=2, 用平面图就 可描绘相的变化. • 对于凝聚体系,压力的影响很小,一般可 忽略不计. • 但温度的影响是相当大的.为了表示温度 对三元体系相图的影响,可用投影的方法, 绘制不同温度下体系的相图.也可借助于 3维动画的技术,绘制三维立体相图
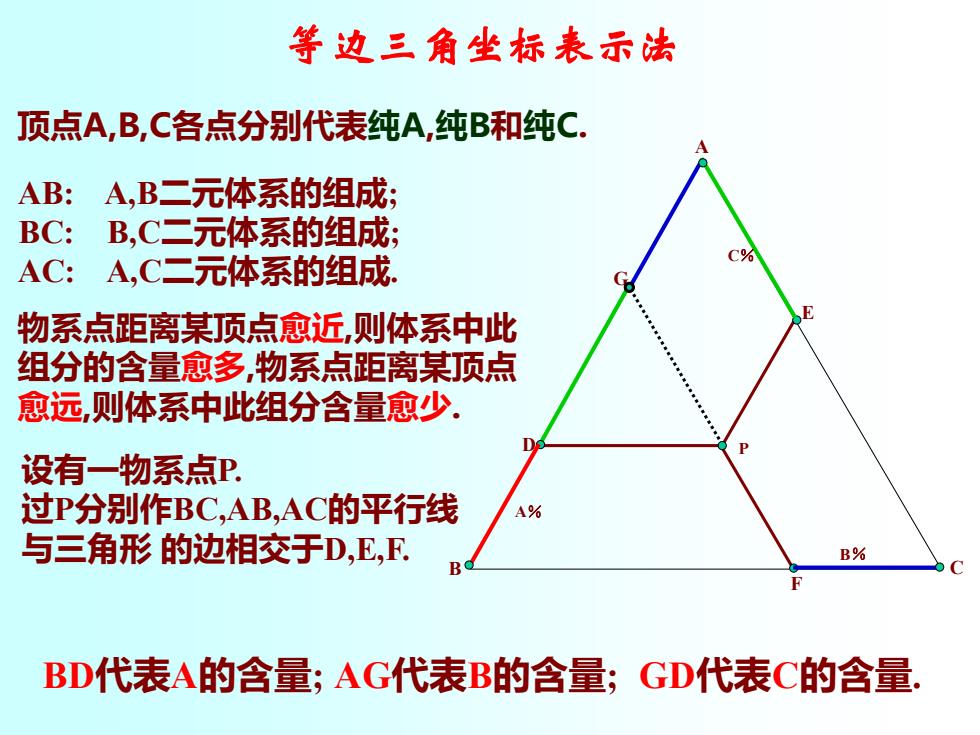
等边三角坐标表示法 顶点A,B,C各点分别代表纯A,纯B和纯C. AB: A,B二元体系的组成; BC: B,C二元体系的组成; AC:A,C二元体系的组成. C% 物系点距离某顶点愈近,则体系中此 组分的含量愈多,物系点距离某顶点 愈远,则体系中此组分含量愈少. 设有一物系点P. 过P分别作BC,AB,AC的平行线 与三角形的边相交于D,E,F. B% BD代表A的含量;AG代表B的含量;GD代表C的含量
等边三角坐标表示法 B C 顶点 A A,B,C各点分别代表纯A,纯B和纯C. AB: A,B二元体系的组成; BC: B,C二元体系的组成; AC: A,C二元体系的组成. 物系点距离某顶点愈近,则体系中此 组分的含量愈多,物系点距离某顶点 愈远,则体系中此组分含量愈少. G F E D P BD代表A的含量; AG代表B的含量; GD代表C的含量. 设有一物系点P. 过P分别作BC,AB,AC的平行线 与三角形 的边相交于D,E,F. B% A% C%
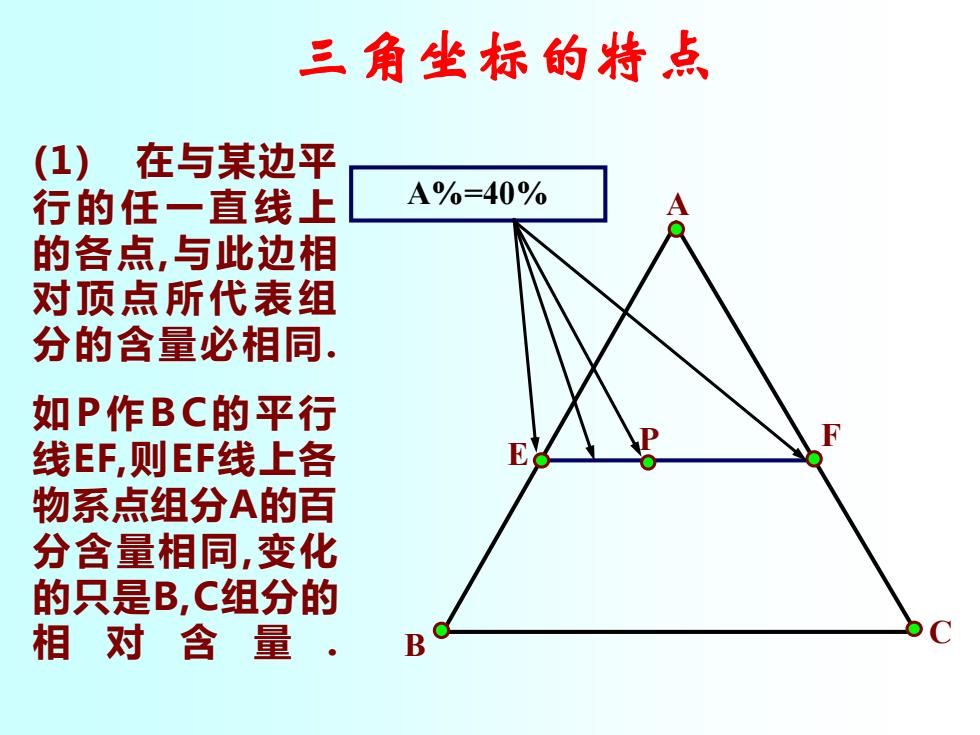
三角坐标的特点 (1)在与某边平 行的任一直线上 A%=40% 的各点,与此边相 对顶点所代表组 分的含量必相同. 如P作BC的平行 线EF,则EF线上各 P 物系点组分A的百 分含量相同,变化 的只是B,C组分的 相对含量 。 B
三角坐标的特点 (1) 在与某边平 行的任 一直 线上 的各点,与此边相 对顶点 所代 表组 分的含量必相同. 如P作B C的平行 线EF,则EF线上各 物系点组分A的百 分含量相同,变化 的只是B,C组分的 相对含量 . C B A P F E A%=40%
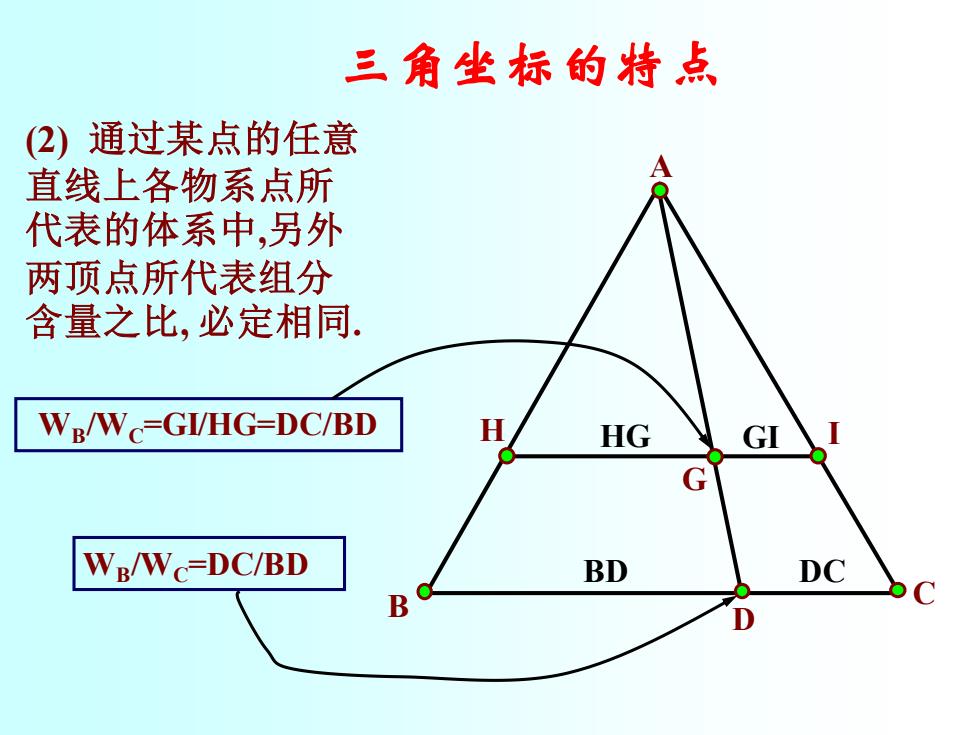
三角坐标的特点 (②)通过某点的任意 直线上各物系点所 代表的体系中,另外 两顶点所代表组分 含量之比,必定相同. WR/Wc=GI/HG=DC/BD H HG GI G Wg/Wc=DC/BD BD DC B D
三角坐标的特点 (2) 通过某点的任意 直线上各物系点所 代表的体系中,另外 两顶点所代表组分 含量之比, 必定相同. D C B A H G I BD DC WB HG GI /WC=GI/HG=DC/BD WB/WC=DC/BD
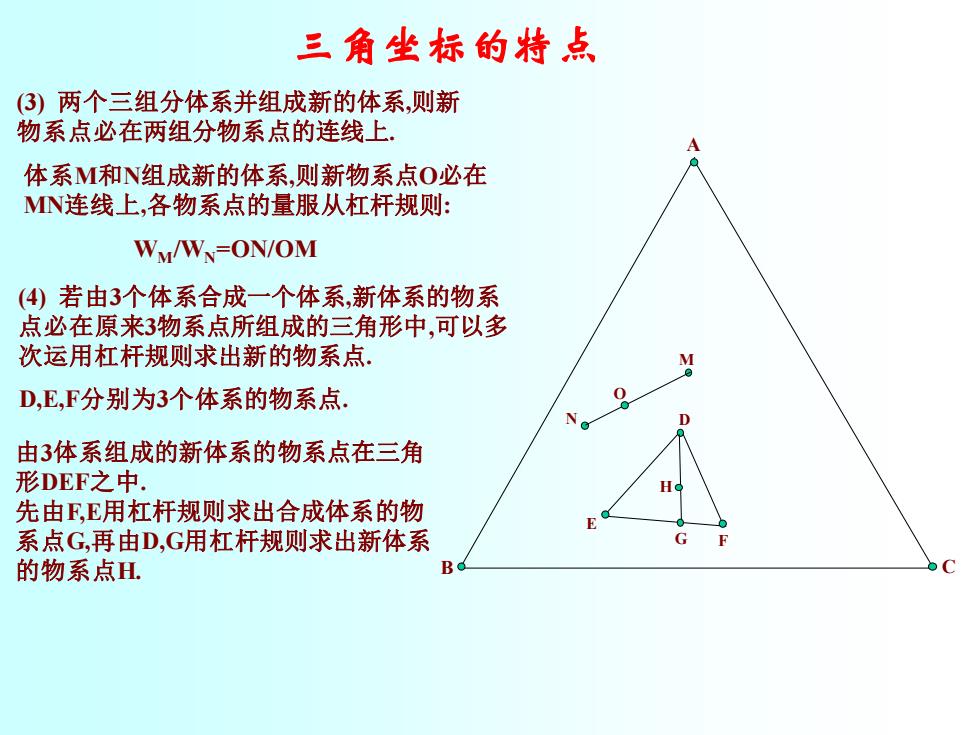
三角坐标的特点 (③)两个三组分体系并组成新的体系,则新 物系点必在两组分物系点的连线上 体系M和N组成新的体系,则新物系点O必在 MN连线上,各物系点的量服从杠杆规则: WM/WN=ON/OM (④)若由3个体系合成一个体系,新体系的物系 点必在原来3物系点所组成的三角形中,可以多 次运用杠杆规则求出新的物系点. D,E,F分别为3个体系的物系点. 。 D 由3体系组成的新体系的物系点在三角 形DEF之中. 先由F,E用杠杆规则求出合成体系的物 系点G,再由D,G用杠杆规则求出新体系 G F 的物系点H
三角坐标的特点 B C A (3) 两个三组分体系并组成新的体系 ,则新 物系点必在两组分物系点的连线上 . 体系 M 和 N组成新的体系 ,则新物系点 O必在 MN连线上 ,各物系点的量服从杠杆规则 : WM/WN=ON/OM M N O (4) 若由 3个体系合成一个体系 ,新体系的物系 点必在原来 3物系点所组成的三角形中 ,可以多 次运用杠杆规则求出新的物系点 . E F DG H D,E,F分别为 3个体系的物系点 . 由 3体系组成的新体系的物系点在三角 形DEF之中 . 先由F,E用杠杆规则求出合成体系的物 系点G,再由D,G用杠杆规则求出新体系 的物系点H
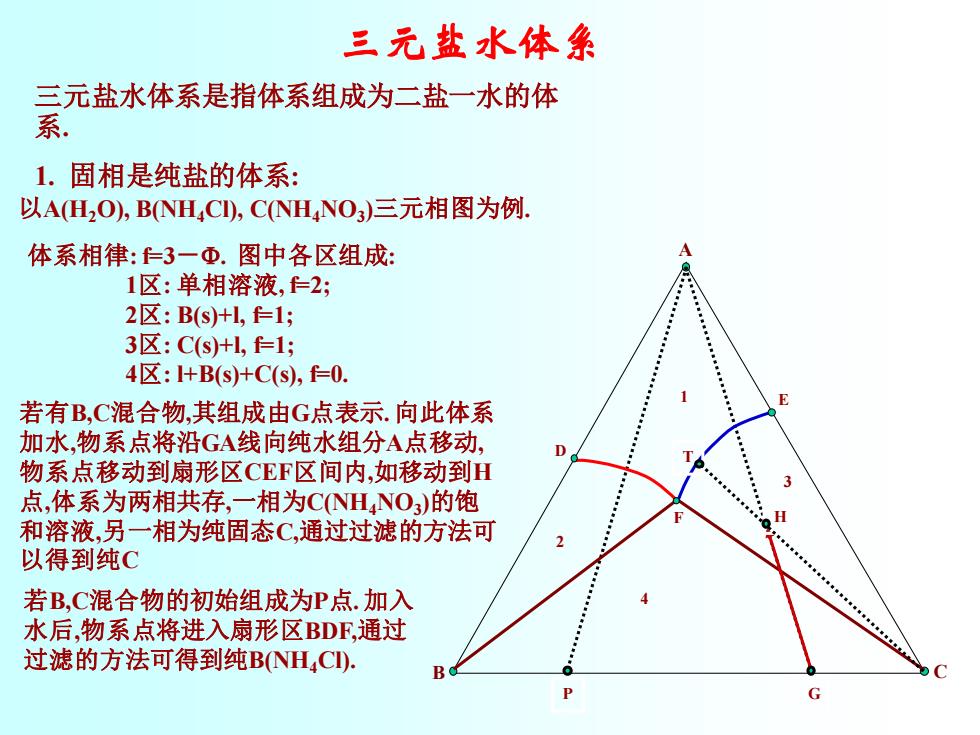
三元盐水体条 三元盐水体系是指体系组成为二盐一水的体 系 1.固相是纯盐的体系: 以A(H2O),BNH,CI),CNH4NO3)三元相图为例. 体系相律:上3一Φ.图中各区组成: 1区:单相溶液,上2; 2区:B(S)tl,=1; 3区:C(s+l,f=1 4区:+B(s)+C(s),f=0. : 1 若有B,C混合物,其组成由G点表示.向此体系 加水,物系点将沿GA线向纯水组分A点移动, 物系点移动到扇形区CEF区间内,如移动到H 点,体系为两相共存,一相为CNH4NO3)的饱 ··! F 和溶液,另一相为纯固态C,通过过滤的方法可 以得到纯C 若B,C混合物的初始组成为P点.加入 水后,物系点将进入扇形区BDF,通过 过滤的方法可得到纯BNHC). D G
三元盐水体系 三元盐水体系是指体系组成为二盐一水的体 系. 1. 固相是纯盐的体系 : 以A(H 2O), B(NH 4Cl), C(NH 4NO 3 )三元相图为例 . 4 3 2 1 体系相律: f=3 - . 图中各区组成: 1 区: 单相溶液, f=2; 2 区: B(s)+l, f=1; 3 区: C(s)+l, f=1; 4 区: l+B(s)+C(s), f=0. B C A P G F E D H T 若有B,C混合物 ,其组成由 G点表示. 向此体系 加水 ,物系点将沿GA线向纯水组分 A点移动, 物系点移动到扇形区CEF区间内 ,如移动到 H 点 ,体系为两相共存 ,一相为C(NH 4NO 3 )的饱 和溶液 ,另一相为纯固态C,通过过滤的方法可 以得到纯 C 若B,C混合物的初始组成为 P 点. 加入 水后 ,物系点将进入扇形区BDF,通过 过滤的方法可得到纯B(NH 4Cl)
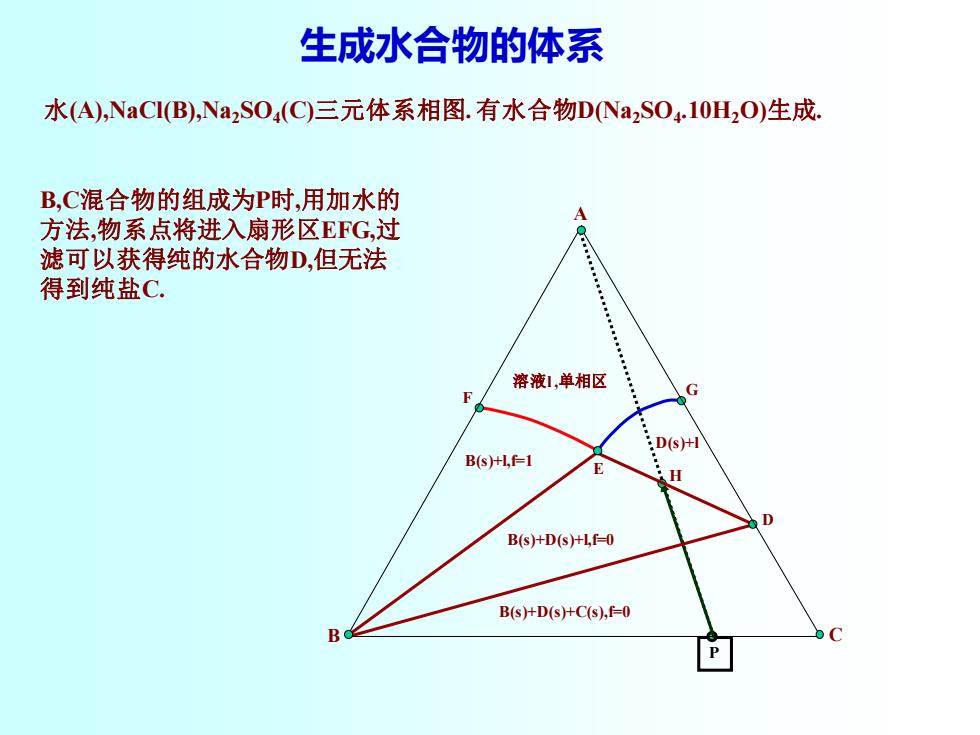
生成水合物的体系 水(A),NaCI(B),Na2S04(C)三元体系相图.有水合物DNa2S0410H2O)生成. B,C混合物的组成为P时,用加水的 A 方法,物系点将进入扇形区EFG,过 滤可以获得纯的水合物D,但无法 得到纯盐C. : : 溶液1,单相区 G D(s十 B(s)+Lf=1 H D B(s)+D(s)+Lf-0 B(s)+D(s)+C(s),f-0
生成水合物的体系 P H G F D E B C A 水(A),NaCl(B),Na2SO4 (C)三元体系相图. 有水合物D(Na2SO4 .10H2O)生成. B,C混合物的组成为P时,用加水的 方法,物系点将进入扇形区EFG,过 滤可以获得纯的水合物D,但无法 得到纯盐C. 溶液l ,单相区 B(s)+l,f=1 D(s)+l B(s)+D(s)+l,f=0 B(s)+D(s)+C(s),f=0
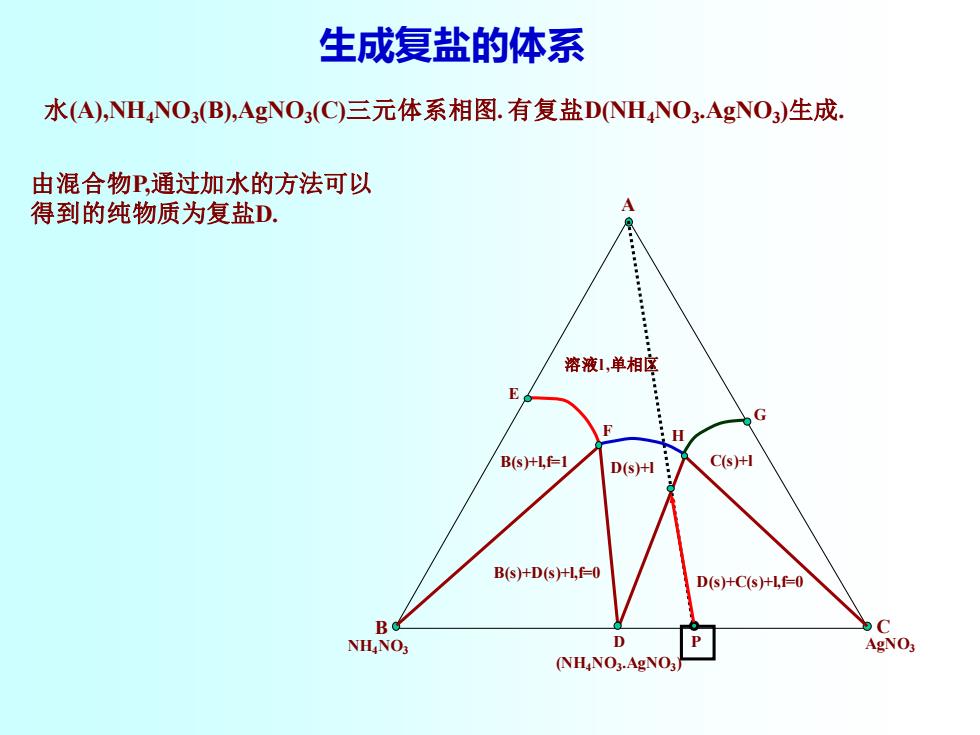
生成复盐的体系 水(A),NHNO3(B),AgNO3(C)三元体系相图.有复盐DNH4NO3AgNO3)生成. 由混合物P,通过加水的方法可以 得到的纯物质为复盐D. A 溶液1,单相客 F H B(s)+l,f=1 D6S)H月 C(s)+I B(s)+D(s)+Lf=0 D(s)+C(s)+Lf-0 B C NHNO3 0 AgNO3 (NHNO3.AgNO3
生成复盐的体系 水(A),NH4NO3 (B),AgNO3 (C)三元体系相图. 有复盐D(NH4NO3 .AgNO3 )生成. B C A NH4NO3 P AgNO3 G F H E D (NH4NO3 .AgNO3 ) 由混合物P,通过加水的方法可以 得到的纯物质为复盐D. 溶液l ,单相区 B(s)+l,f=1 C(s)+l B(s)+D(s)+l,f=0 D(s)+C(s)+l,f=0 D(s)+l