
3.4 分块矩阵
LOGO 3.4 分块矩阵

·分块矩阵的定义 分块矩阵的运算 ·分块思想的应用
• 分块矩阵的定义 • 分块矩阵的运算 • 分块思想的应用

一、 分块矩阵的定义 定义将矩阵A用一些横线和竖线分成许多小矩阵, 每一个小矩阵称为矩阵A的子块,以子块为元素的 矩阵称为分块矩阵】 011 alk 0 0 0 例1 0 D aki akk C11 Clk b11 bis Cs1 Csk bss
一、分块矩阵的定义

一、 分块矩阵的定义 例2矩阵 011 a12 . ain A= a21 a22 a2n : ami am2 amn 按行分块可表示为 A1 A= Am 按列分块可表示为 A=(B1,B2,.,B)
一、分块矩阵的定义

二、分块矩阵的运算 1、分块加法 设A,B是两个同型矩阵,且分块方法一致,得 A11 A12 Aia B11 B12 Bi A= A21 A22 A2a B21 B22 B2a .: ,B Api Ap2 Apa Bpi Bp2 . Bpa 则 A11+B11A12+B12 . A1q+Biq A+B= A21+B21 A22+B22 A2q+B2q Api+Bp1 Ap2 +Bp2 Apa Bpa
二、分块矩阵的运算
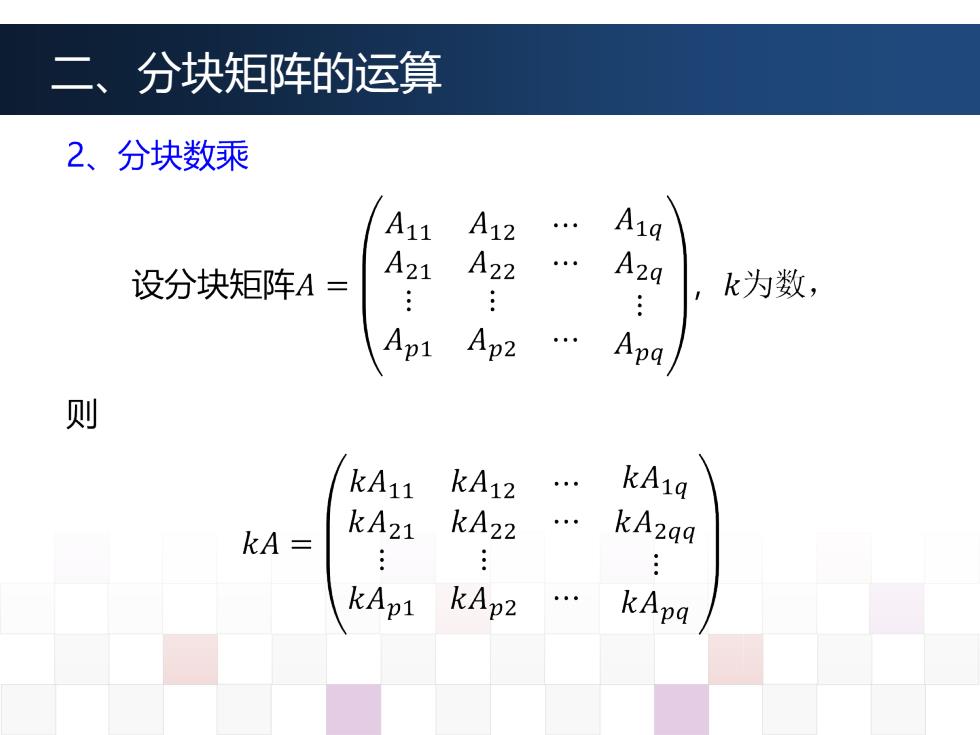
二、分块矩阵的运算 2、分块数乘 A11 A12 . Aia 设分块矩阵A= A21 A22 A2a k为数, Apt Apz Apa 则 kA11 kA12 . kAia kA= kA21 kA22 kAzqa : kApi kAp2 kApa
二、分块矩阵的运算

二、分块矩阵的运算 3、分块乘法 设A=(aik)mxs,B=(bkj)sxn,对A的列的分法与B的行的 分法一致,记为: A11 A12 . A1t B11 B12 Bia A= A21 A22 A2t ,B= B21 B22 B2a Ap1 Ap2 Apt Bt Bt2 Bta 其中Ak是m:×Sk小矩阵,Bkj是sk×n小矩阵
二、分块矩阵的运算

二、分块矩阵的运算 3、分块乘法 于是有 C11 C12 Cia C=AB= C21 C22 C2a Cp1 Cp2 Cpa 其中 Cy AnB+ArBay+AnBuAnBx k=1 (1=1,2,.,pj=1,2,.,q)
二、分块矩阵的运算

二、分块矩阵的运算 例3设 A= 10 1 1 0 2 1 1 求AB
二、分块矩阵的运算

二、分块矩阵的运算 4、分块转置 设 A11 A12 Aia A= A21 A22 A2a Api Ap2 . Apa 则 疆三隔 A21 AT- A32 Ap2 Apa
二、分块矩阵的运算