
试卷代号:1024 座位号☐ 中央广播电视大学2011一2012学年度第二学期“开放本科”期末考试 信号处理原理试题 2012年7月 题 号 二 三 四 五 六 总 分 分 数 得 分 评卷人 一、单项选择题(每小题5分,共25分) 1.偶周期信号的傅立叶级数不可能有( 。 A.余弦项和直流项 B.正弦项 C.直流项 D.余弦项 2.卷积积分f(t+5)*6(t一4)的计算结果是()。 A.f(t+1) B.f(t-1) C.f(t-9) ,D.f(t+9) 3.下列说法不正确的是()。 A)通过三角函数相乘可以使信号的频谱得到搬移 B.非因果信号在时间零点之前不可能有值 C.傅立叶频谱是冲激函数的信号一定是直流信号 D.信号的等效脉宽和等效带宽不能被同时压缩 10z 4.已知X(e)=2-)z-2)其反变换x(m)的第2项x1)=()。 A.0 B.70 C.10 D.1 188
试卷代号 座位号 中央广播电视大学 0 11 2学年度第二学期"开放本科"期未考试 信号处理原理试题 2012 年7 题号 /儿、• 总分 分数 得分|评卷人 一、单项选择题{每小题 5分,共 5分) B.J(t- 1) D. J(t+9) 1.偶周期信号的傅立叶级数不可能有( )。 A. B. 正弦 c. 直流项 • 2. 卷积积 十5) 铃 0 (( 算结果 )。 A. J((+ 1) c. J(t - 9) 3. 'f列说法不正确的是( )。 Aj 相乘 信号 搬移 B.非因果信号在时间零点之前不可能有值 c.傅立叶频谱是冲激函数的信号一定是直流信号 D. 脉宽 等效带宽不能 知Xω=(z 一2) ·其反变换巾)的第 )。 188 A.O c. 10 B.70 D.l

5.Z[(-3)u(n)]=()。 A2十3 B3 C.3 D.:-3 得 分 评卷人 二、判断题(每小题3分,共15分) 6.saoa=14. 7.Sa信号的傅立叶变换是奇函数。 8.时不变系统的响应与激励施加的时刻是没有关系的。 9.信号时移只会对幅度谱有影响。 10.单位阶跃序列的Z变换结果是常数。 得 分 评卷人 三、填空题(每小题4分,共20分)】 11.比较FS和FT可知: 的频率定义域为离散频率, 的频率定义域连 续频率,整个频率轴。 12.FT的变换核是 13.∫e.2tδ(t)dt= 14.序列x(n)为右边序列,其Z变换为X(z),x(n)向右平移1个单位后再求取双边Z变 换,结果是Zx(n-1)]= 15.Z[(-2)nu(n)+6(n)]= 189
5.Z[(-3)nu ( n ) ] = ( )。 A-4τB. →一D. 1 z -z • 3 -.. 得分 l评卷人 二、判断题{每小题 6. [缸 7. Sa 8. 不变 的 响 励施加 9. 10. 位 阶 的Z 变换结果是 得分|评卷人 三、填空题{每小题 > 1 1. 较FS 和FT 续频率,整个频率轴。 12. FT 核是 13. (t 的频率定义域为离散频率, 的频率定义域连 14. 边序 其Z 变换 右平移 个单 求取 换,结果是 15. Z[(-2)n 189

得分 评卷人 四、证明题(10分) 16.证明以下关系成立: [3"nu(n)]= 3 学-) 2 得 分 评卷人 五、计算题(每小题10分,共20分) l7.求信号x(t)=sin2t的傅立叶变换。 18.设一阶离散系统的差分方程为ay(n)一y(n一1)=cx(n),求: (1)该系统的传递函数H(z); (2)输人为6(n)时系统的零状态响应。 得分评卷人 六、作图题(10分) 19.画出离散信号u(n);6(n一1)波形。 190
得分|评卷人 四、证明题 16. 明 以 成立 nu n -z-3 Z 得分|评卷人 五、计算题{每小题 0分,共 0分) 17. =sin2t 18. 阶离 方程 I) =cx( (1)该系统的传递函数 ; (2) 得分 i评卷人 六、作固题 19. I) 190

试卷代号:1024 中央广播电视大学2011一2012学年度第二学期“开放本科”期末考试 信号处理原理 试题答案及评分标准 (供参考) 2012年7月 一、单项选择题(每小题5分,共25分) 1.B 2.A 3.B 4.C 5.A 二、判断题(每小题3分,共15分)】 6.错误 7.错误 8.正确 9.错误 10.错误 三、填空题(每小题4分,共20分) 11.FS FT 12.e-jot 13.0 14.x-1X(z) 15.2z+2 z+2 四、证明题(10分) 16.证明: 根据定义:Y[a"x(n)]= a"x(n)zm n0 =总) (6分) 而X()=[x(n)]=[nu(n)]=(z- 2 所以[3"nu(n)]=X(z/3)= (号-D (4分) 五、计算题(每小题10分,共20分) 17.求信号x(t)=sin2t的傅立叶变换 解:z()=sin2L=e0-en 2 (3分) 因为1+2π6(w) (2分) 191
试卷代号 中央广播电视大学 2 0 11 2012 年度 第 二学期 开放 末考 信号处理原理试题答案及评分标准 (供参考) 2012 年7 一、单项选择题{每小题 1. B 2. A 3. B 二、判断题{每小题 6. 误7. 误8. 三、填空题{每小题 11. FS FT 12. e- 13.0 14. Z-l X(z) 2z+2 15. 四、证明题(1 16. 根据定义 anx(n)z-n 0=0 =ZKn)(?) =X( a =~[x(n)J =~[nu( • • z 所以 = X (?一 1 ) 五、计算题(每小题 2 0 17. t) = sin2t J t ~J 因为 ~27!'0' 4. C 9. 5. A 10. 错误 (6 (4 (3 (2 191
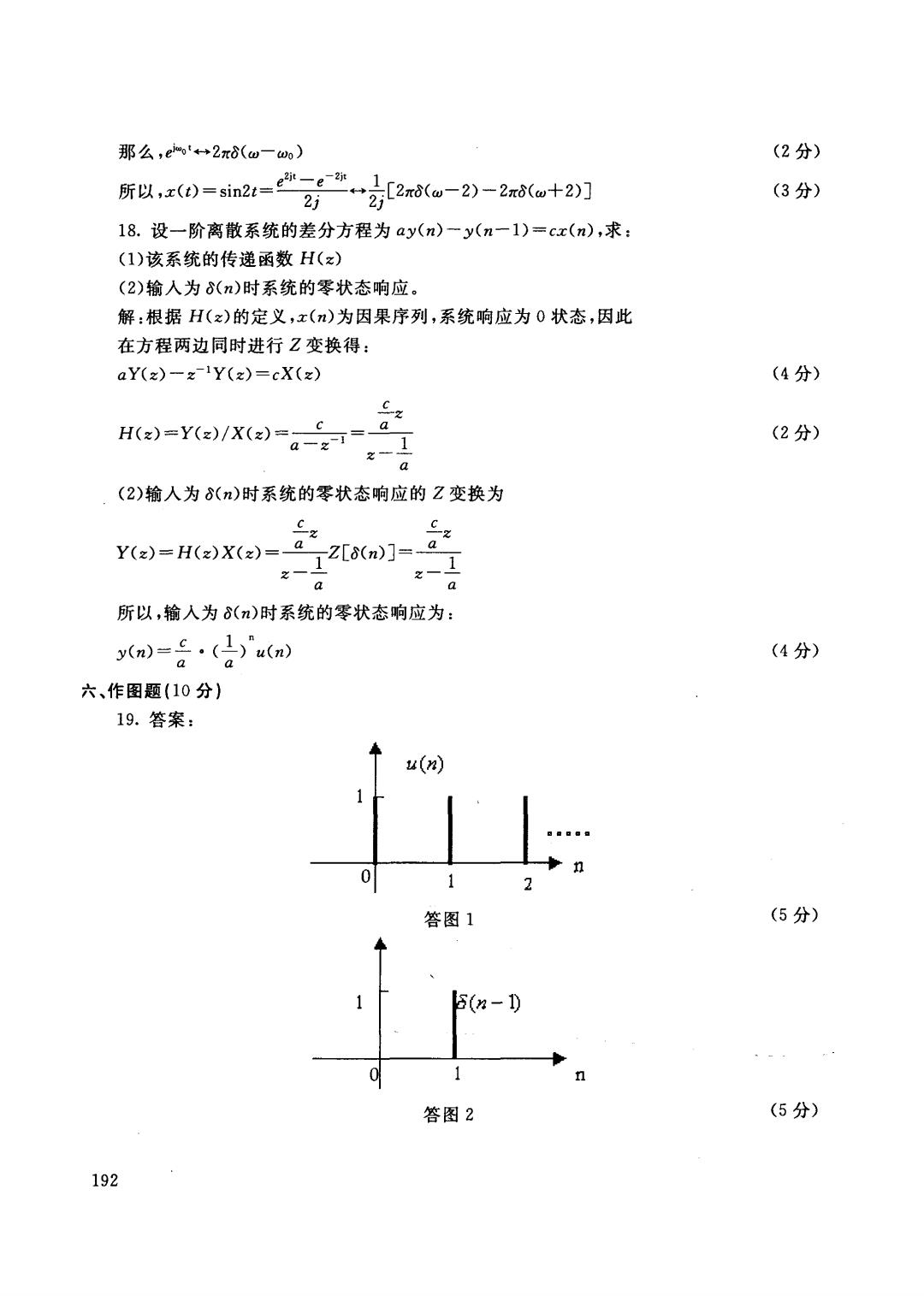
那么,emo'+2π6(w一w) (2分) 所以,x(0=in24=,。n号[2xd(u-2)-2mCo十2] 2+ 21 (3分) 18.设一阶离散系统的差分方程为ay(n)一y(n一l)=cx(n),求: (1)该系统的传递函数H(z) (2)输人为6(n)时系统的零状态响应。 解:根据H(z)的定义,x()为因果序列,系统响应为0状态,因此 在方程两边同时进行Z变换得: aY(z)-z-1Y(z)=cX(z) (4分) H(x)=Y(x)/X()=c (2分) a (2)输人为8(n)时系统的零状态响应的Z变换为 Y(x)=H(z)X(x)=-aZ[8(n)]=-@ 1 2一 7 a 所以,输人为8()时系统的零状态响应为: y(n)=£.(2)”u(m) n (4分) a 六、作图题(10分) 19.答案: u(n) n 答图1 (5分) 5(8-1) 、 1 n 答图2 (5分) 192
那么, ]=-a 1 a a 所以,输人为 )时系统的零状态响应为 u n c-a 1-nun y n (4 六、作图题 19. u n h ' a • a a a n 2 答图 (5 (n-I) t "7L __ n 答图 (5 192