试卷代号:1002 座位■■ 中央广播电视大学2011一2012学年度第二学期“开放本科”期末考试(半开卷) 计算机数学基础(1)试题 2012年7月 题 号 二 三 四 总 分 分 数 得 分 评卷人 一、单项选择题(每小题4分,共20分) 1.下列各语句中是命题的为( ) A.x+5 的哈斯图是(). 图 W
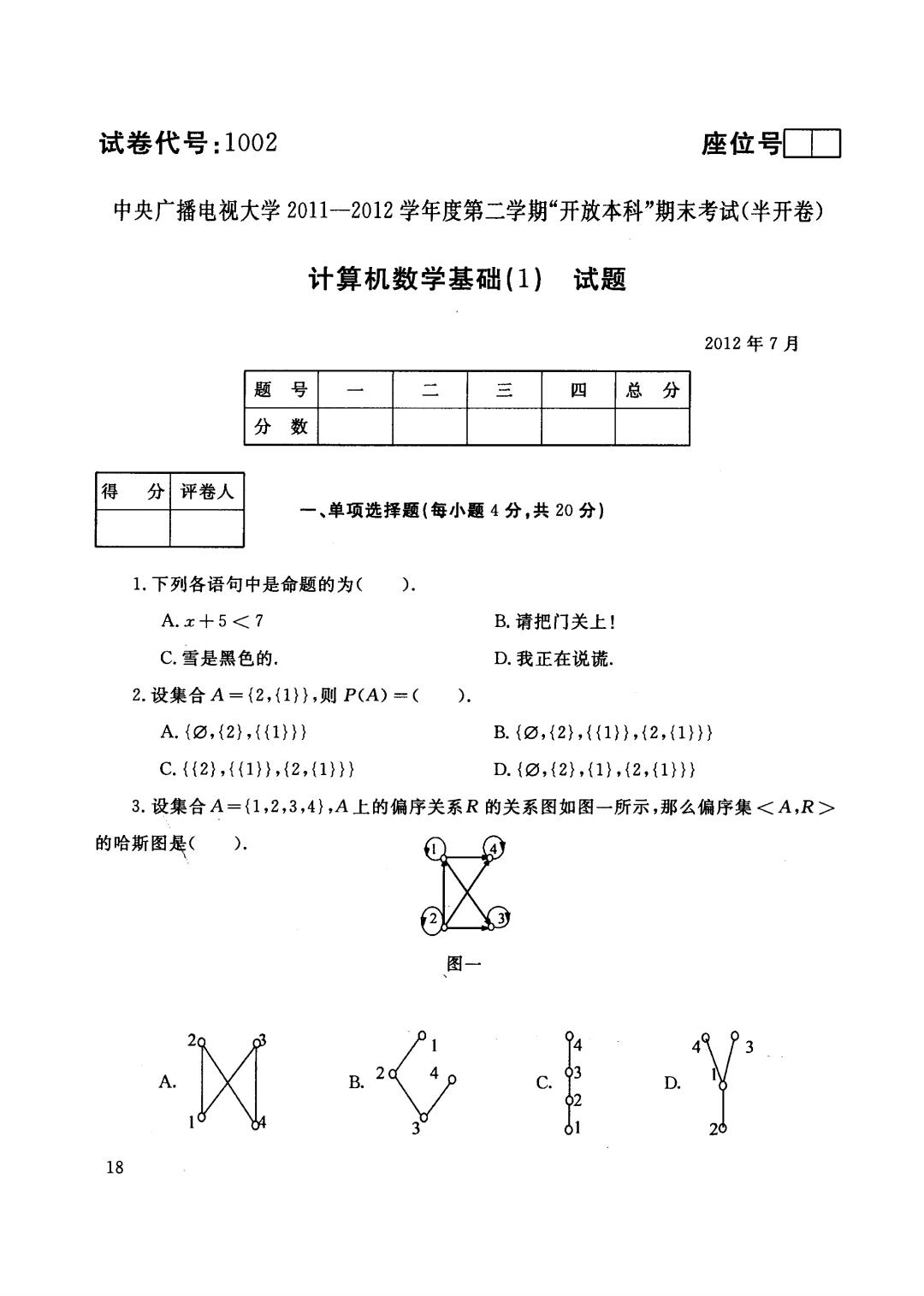
试卷代号 座位号 中央广播电视大学 2012 , 2012 年7 题号 '植-事 J a ‘ A -由... ' 总分 分数 得分|评卷人 -、单项选择题{每小题 1. 下列 ). A.x+5 < 7 B. c. 雪是 D. 2. {2 ,{1}} -( ). A. {0, { 2} , { {I} }} B. {白, }, { { }, 2, c. {{2} , { {1 }}, {2, {1}}} D. {0 , { 2} , {1}, {2 , {1}}} 3. {1 ,2 ,3 ,4} 序集 的哈斯图是( ). 图一 3 2 c. D. 2 A. + 18

4.设图G=,则下列结论成立的是(). A.deg(V)=2E B.deg(V)=E C.deg() D会dego)=lEl 5.无向完全图K4是(). A.哈密顿图 B.欧拉图 C.树 D.非平面图 得分 评卷人 二、填空题(每小题4分,共20分) 6.设P:明天下雨,Q:我去书店.则将命题“如果明天不下雨,我就去书店”符号化 为 7.设个体域D={a,b,c},公式VxF(x)→3yG(y)消去量词化为 8.集合Ac0当且仅当 9,数列{2,3,3,4}不能构成无向简单图的度数列,此命题的真值为 10.设G是连通平面图,v,e,r分别表示G的结点数,边数和面数,则v,e和r满足的关系式 是 得 分 评卷人 三、化简计算题(每小题10分,共50分)】 11.设P是二元谓词符号,给定解释I如下: 个体域D={a,b},P(a,a)=P(a,b)=0,P(b,a)=P(b,b)=1 求3xyP(x,y)在解释I下的真值.(要求写出过程) 12.设集合A={a,b,c,d,e},B={b,d,e},C={a,b,d},求(A-B)⊕(BUC). 13.设集合A={0,1,2,3,4},定义A上的二元关系R为: R={|x,y∈A∧(x=yVx十y∈A)》 试写出二元关系R的集合表达式,并指出R具有的性质. 19
4. = 1 ,y /I. (x = y V x +y eA)} 试写出二元关系R的集合表达式,并指出R具有的性质. 19
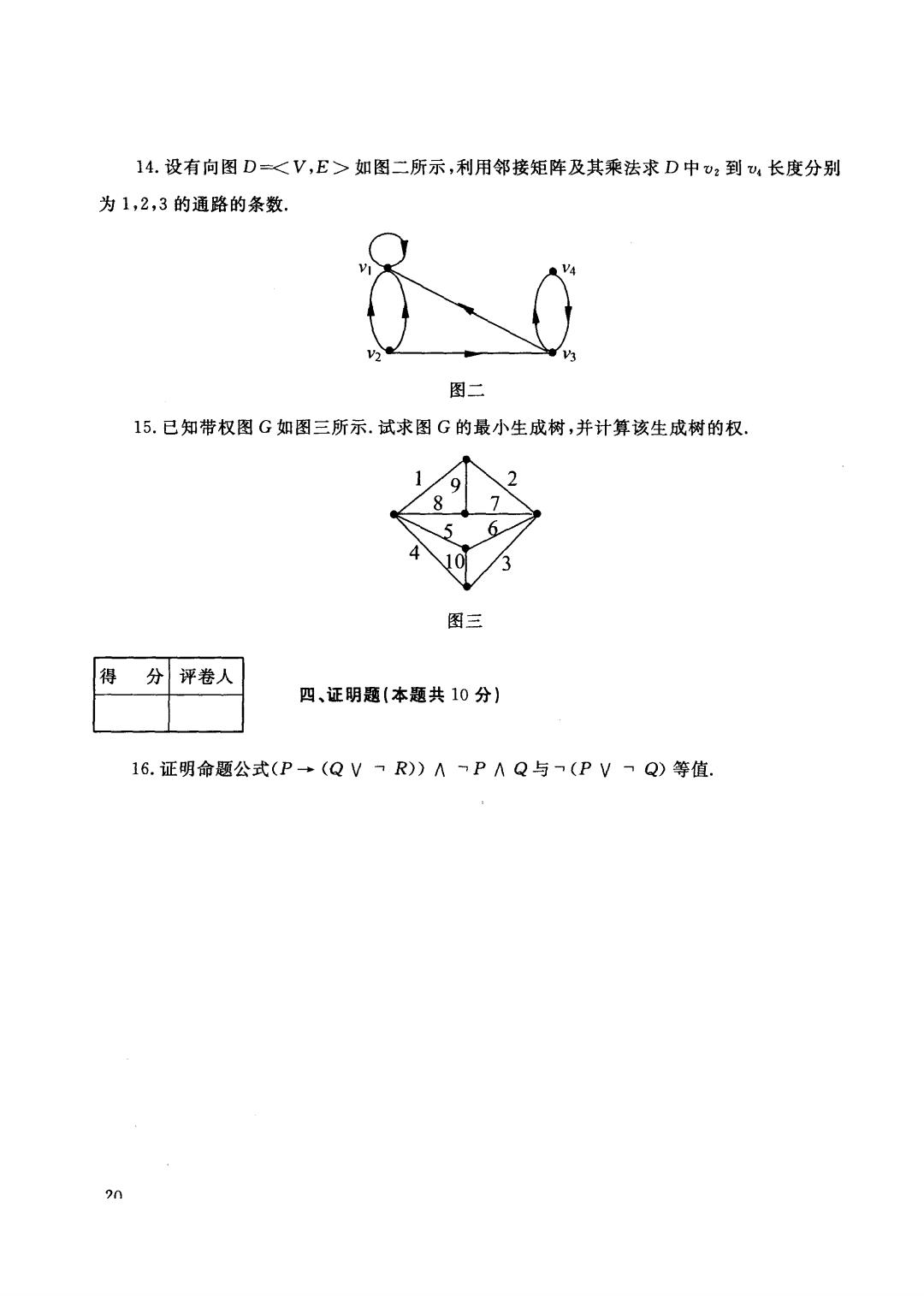
14.设有向图D=如图二所示,利用邻接矩阵及其乘法求D中v2到U4长度分别 为1,2,3的通路的条数 图二 15.已知带权图G如图三所示.试求图G的最小生成树,并计算该生成树的权. 图三 得 分 评卷人 四、证明题(本题共10分) 16.证明命题公式(P(QV一R))ΛP∧Q与(PVQ)等值. 20
14. 二所 长度 3的通路的条数, 图二 15. 图G 三所 图G 8 图三 得分|评卷人 四、证明题{本题共 16. V -, R») 1\ I P A -, (P V -, Q) 等值 ?11

试卷代号:1002 中央广播电视大学2011一2012学年度第二学期“开放本科”期末考试(半开卷) 计算机数学基础(1) 试题答案及评分标准 (供参考) 2012年7月 一、单项选择题(每小题4分,共20分) 1.C 2.B 3.D 4.C 5.A 二、填空题(每小题4分,共20分) 6.P→Q 7.(F(a)∧F(b)AF(c)→(G(a)VG(b)VG(c) 8.A=☑ 9.1 10.v+r-e=2 三、化简计算题(每小题10分,共50分) 11.3x VyP(x,y)VyP(a,y)V VyP(b,y) (4分) (P(a,a)A P(a,6))V(P(b,a)A P(b,b)) (8分) 台(0Λ0)V(1∧1)台1 (10分) 12.(A--B)(BU C)=((a,b,c,d,e)-(b,d,e))((b,d,e)U(a,b,d)) ={a,c}⊕{a,b,d,e》 (4分) =(a,b,c,d,ek-fa) (8分) ={b,c,d,e} (10分) 13.由题设, R=IAU{,,,,,, ,,,,,} (7分) 易知,R具有自反性和对称性。 (10分) 21
试卷代号 0 0 中央广播电视大学 11 2012 年 度第二学期 开放 期 末考 半开 计算机数学基础 )试题答案及评分标准 (供参考) 2012 年7 一、单项选择题{每小题 4分,共 0分) I. C 2. B 3. D 4. C 5. A 二、填空题(每小题 4分,共 0分} 6. --, P • Q 7. (F(a) F(e» •(G(a) V G(b) V G(e» 8.A=0 9. 1 10. v+r-e=2 三、化简计算题{每小题 0分,共 0分} 11. 3x 'rJ V VyP(b ,y) V (P(b 八P(b ,b» A0) V (1八1)件 12. (A\-B) €a (B U C) =({a ,b ,e ,d ,e} 一{b ,d ,e}) €a ( {b , d , e } U {a ,b ,d}) =怡,c} €a = {a ,c ,e}. 一{a} = {b , c ,d , e } 13. R=IA U {, , , , , , , , , , , } 易知 称性 (4 (8 (1 (4 (8 (1 (7 (1 21

14.图D的邻接矩阵为 10007 201 0 A(D)= (3分) 1001 0010 且 100 01 1000] 3 00 1 301 0 A2(D)= ,A3(D)= (8分) 101 0 2001 100 1 101 0」 由A(D),A2(D),A3(D)中的a24=0,a经=1,a=0知所求通路的条数分别是0条、1条 和0条。 (10分) 15.做法如下: ①选边1; ②选边2; ③选边3; ④选边5; ⑤选边7 解答图一 于是,最小生成树如解答图一中粗线所示.· (8分) 最小生成树的权数为:1+2+3+5+7=18. (10分) 注:采用破圈法参照给分, 四、证明题(本题共10分) 16.(P→(QVR)∧P∧Q台(PV(QVR))∧P∧Q (mP∧PΛQ)V(Q∧P∧Q)V(R∧P∧Q) (3分) 台(7P∧Q)V(P∧Q)V(PAQ∧R)(6分) 台P∧Q 台(PVQ) (10分) 注:采用其他方法参照给分. 22
14. 图D 接矩 100 0 2 O 1 O A(D) = I (3 1 O O 1 O 1 O N(D)= 100 0 300 1 101 0 100 1 ,N (D) = 1 000 3 0 1 0 200 1 1 0 1 0 (8 由 A ,N (D) ,N (D) 15. 法如下 ①选边 ; ②选边 ③选边 ; ④选边 ⑤选边 于是,最小生成树如解答图一中粗线所示. 最小生成树的权数为 十2 十3 + 5+7 = 18. 注 z采用破圈法参照给分. 四、证明题(本题共 16. (P• (Q V --, --, 伸(--, V (Q V --'R» --, /\ Q P八--, p八 (Q --, --, --, (3 仲(--, V (--, V (--, P /\ Q /\ :'R) (6 (1 解答图一 (8 (1 件--, p八 仲--, (P V --, Q) (1 注:采用其他方法参照给分. 22