
电子科技大学研究生《机器学习》课程 第3讲线性模型 Lecture3 Linear Models 郝家胜(Jiasheng Hao) Ph.D.,Associate Professor Email:hao@uestc.edu.cn School of Automation Engineering,Center for Robotics University of Electronics and Science of China,Chengdu 611731 参考:《机器学习》周志华
电子科技大学研究生《机器学习》课程 Email: hao@uestc.edu.cn School of Automation Engineering, Center for Robotics University of Electronics and Science of China, Chengdu 611731 郝家胜 (Jiasheng Hao) Ph.D., Associate Professor 参考:《机器学习》周志华 第3讲 线性模型 Lecture3 Linear Models
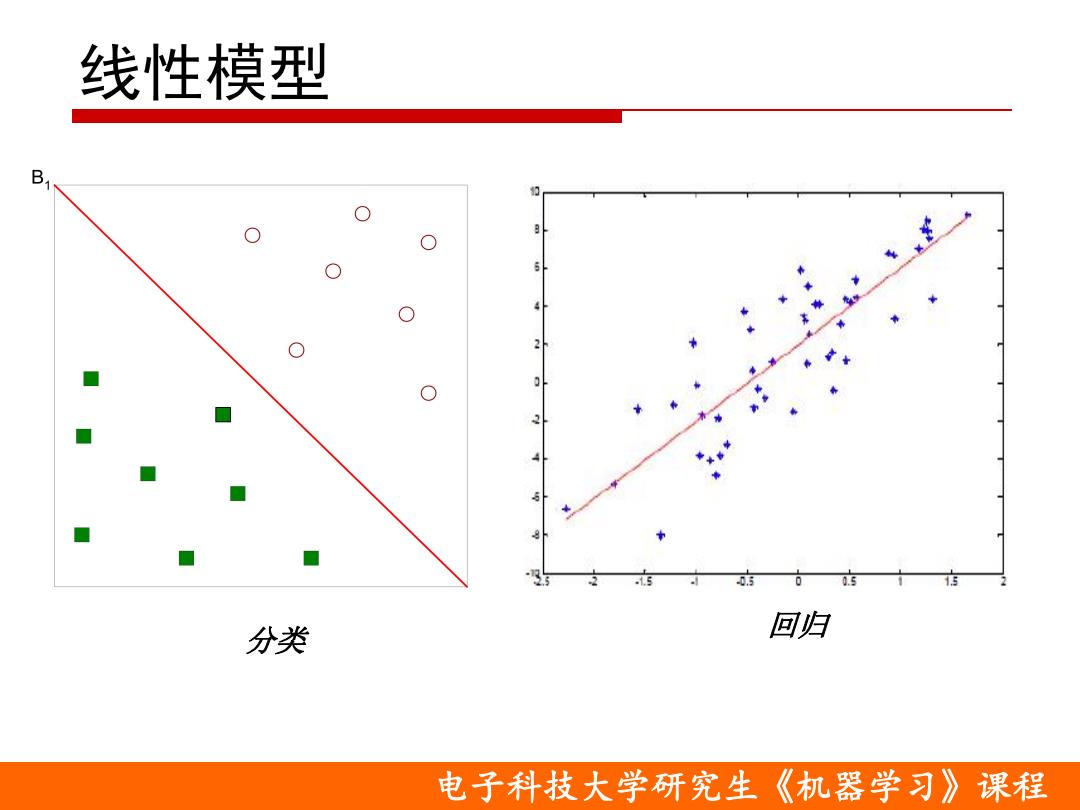
线性模型 0. 分类 回归 电子科技大学研究生《机器学习》课程
电子科技大学研究生《机器学习》课程 线性模型 分类 回归

本章目标 ▣理解对数几率回归 ▣理解线性判别分析 口了解多分类学习 口了解类别不平衡问题 口掌握线性回归
q 理解线性判别分析 q 了解多分类学习 q 理解对数几率回归 q 掌握线性回归 q 了解类别不平衡问题

目录 口线性回归 ■最小二乘法 口二分类任务 ■ 对数几率回归 ■线性判别分析 口多分类任务 ■ 一对一 一对其余 ■ 多对多 ▣ 类别不平衡问题 电子科技大学研究生《机器学习》课程
电子科技大学研究生《机器学习》课程 目录 o 线性回归 n 最小二乘法 o 二分类任务 n 对数几率回归 n 线性判别分析 o 多分类任务 n 一对一 n 一对其余 n 多对多 o 类别不平衡问题

基本形式 口线性模型试图学得一个通过属性的线性组合来进行预测 的函数。 一般形式为 f (x)=w1x1 +W222 +...Waxd +b C三 (C1;x2;.·.;xd)是由属性描述的示例,其中C是C在第个属性上的 取值 口向量形式 f(x)=wx+b 其中w=(w1;w2;;wa) 电子科技大学研究生《机器学习》课程
电子科技大学研究生《机器学习》课程 基本形式 o 线性模型试图学得一个通过属性的线性组合来进行预测 的函数。 一般形式为 是由属性描述的示例,其中 是 在第 个属性上的 取值 o 向量形式 其中

线性模型优点 形式简单、易于建模,但却蕴含着一些重要的 基本思想 口可解释性强:w直观表达了各属性在预测中的 重要性 ▣非线性模型的基础 ■ 引入层级结构或高维映射 ▣一个例子 综合考虑色泽、根蒂和敲声来判断西瓜好不好 其中根蒂的系数最大,表明根蒂最要紧;而敲声的 系数比色泽大,说明敲声比色泽更重要 f好瓜(c)=0.2·x色泽十0.5·x根蒂十0.3·x敲声+1 电子科技大学研究生 《机器学习》课程
电子科技大学研究生《机器学习》课程 线性模型优点 o 形式简单、易于建模,但却蕴含着一些重要的 基本思想 o 可解释性强:w直观表达了各属性在预测中的 重要性 o 非线性模型的基础 n 引入层级结构或高维映射 o 一个例子 n 综合考虑色泽、根蒂和敲声来判断西瓜好不好 n 其中根蒂的系数最大,表明根蒂最要紧;而敲声的 系数比色泽大,说明敲声比色泽更重要

线性回归 ▣ 给定数据集D={(c1,y1),(c2,y2),.·,(cm,ym)} 其中c=(c1;x2;.;xd)∈R 口线性回归(linear regression)目的 学得一个线性模型以尽可能准确地预测实值输出标记 离散属性处理 ■有“序”关系 ▣连续化为连续值 无“序”关系 ▣有k个属性值,则转换为k维向量 电子科技大学研究生《机器学习》课程
电子科技大学研究生《机器学习》课程 线性回归 o 给定数据集 其中 , o 线性回归(linear regression)目的 n 学得一个线性模型以尽可能准确地预测实值输出标记 o 离散属性处理 n 有“序”关系 p 连续化为连续值 n 无“序”关系 p 有k个属性值,则转换为k维向量

线性回归 ▣单一属性的线性回归目标 f(x)=wx:+b使得∫(x)≈y 口参数/模型估计:最小二乘法 (least sauare method) 10 .Data curve fit 9 (w",b)=argmin>(f (xi)-y:)2 8 (w,b) 2=1 6 argmin∑(-wax,-b)2 (w,b) i=1 电子科技大学研究生《机器学习》课程
电子科技大学研究生《机器学习》课程 线性回归 o 单一属性的线性回归目标 o 参数/模型估计:最小二乘法(least square method) 使得

线性回归-最小二乘法 ▣最小化均方误差 E(u,)=∑(g- wxi-b)2 i=1 口分别对和b求导,可得 =2∑-∑-4 ∂w 2=1 -(w--) ab 电子科技大学研究生《机器学习》课程
电子科技大学研究生《机器学习》课程 线性回归 - 最小二乘法 o 最小化均方误差 o 分别对 和 求导,可得

线性回归-最小二乘法 ▣得到闭式(closed-form)解 m ∑(x-) i=1 W= m -品 -1 m 品 (yi -wc) 其中 m 元 -IS Xi i=1 电子科技大学研究生《机器学习》课程
电子科技大学研究生《机器学习》课程 线性回归 - 最小二乘法 o 得到闭式(closed-form)解 其中