
3.柱下条形基础、筏形和箱形基础 雨容提要 √弹性地基上梁的分析 √柱下条形基础的常用计算方法 √筏形基础设计计算方法 √箱形基础设计计算方法 2
3.柱下条形基础、筏形和箱形基础 2 内容提要 ü弹性地基上梁的分析 ü柱下条形基础的常用计算方法 ü筏形基础设计计算方法 ü箱形基础设计计算方法

3.柱下条形基础、筏形和箱形基础 3.1概述 ■优点:埋深较大、可提高地基承载力、增大基础抗滑稳定 性、并可利用补偿作用减小基底附加应力、减轻不均匀沉 降、减小上部结构次应力、提供地下空间 ■缺点:技术要求与造价较高、施工中需处理大基坑、深开 挖等问题,且箱基的地下空间利用不灵活 ■计算方法: √若按常规设计方法(仅满足静力平衡条件),误差较大; √应考虑上部结构一基础一地基相互作用,采用适当方法; √可仅考虑地基一基础相互作用,采用弹性地基上的梁、板 模型计算 3
3.柱下条形基础、筏形和箱形基础 3 n 优点:埋深较大、可提高地基承载力、增大基础抗滑稳定 性、并可利用补偿作用减小基底附加应力、减轻不均匀沉 降、减小上部结构次应力、提供地下空间 n 缺点:技术要求与造价较高、施工中需处理大基坑、深开 挖等问题,且箱基的地下空间利用不灵活 n 计算方法: ü 若按常规设计方法(仅满足静力平衡条件),误差较大; ü 应考虑上部结构-基础-地基相互作用,采用适当方法; ü 可仅考虑地基-基础相互作用,采用弹性地基上的梁、板 模型计算
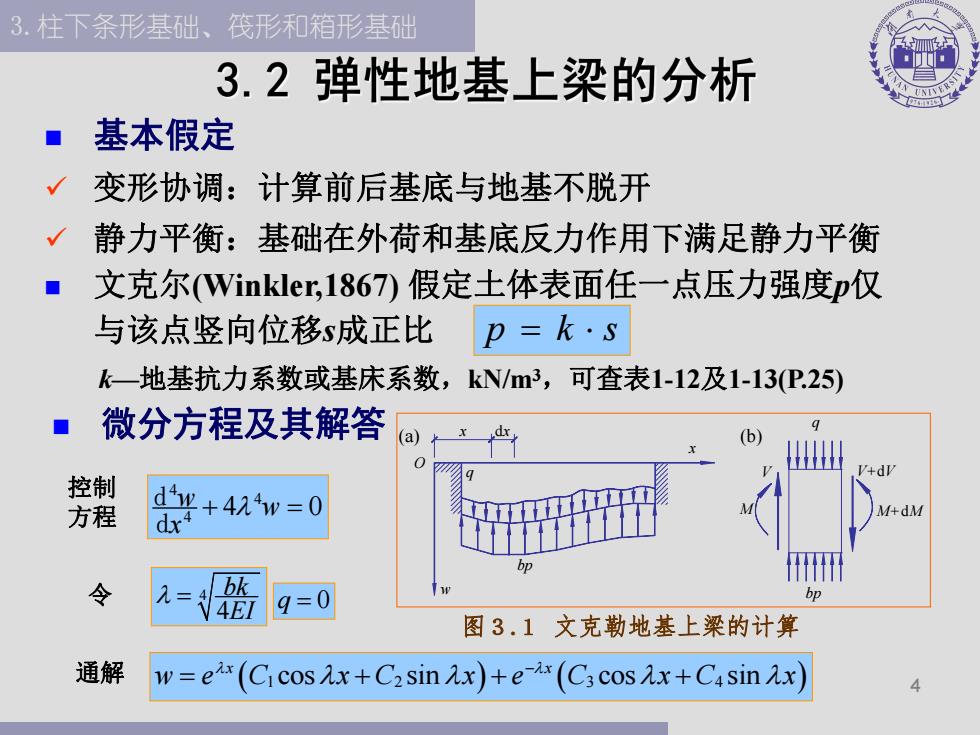
3.柱下条形基础、筏形和箱形基础 3.2弹性地基上梁的分析 基本假定 变形协调:计算前后基底与地基不脱开 √静力平衡:基础在外荷和基底反力作用下满足静力平衡 文克尔(Winkler,,l867)假定土体表面任一点压力强度p仅 与该点竖向位移s成正比 p=k·s k-地基抗力系数或基床系数,kN/m3,可查表1-12及1-13P.25) 微分方程及其解答 dx (b) V+dV 控制 方程 +424w=0 +dM bp 令 bk 1=4E 9=0 bp 图3.1文克勒地基上梁的计算 通解 w=e4x (Ci cos x+C2sin x)+e 4*(C3 cos x+Casin x)
3.柱下条形基础、筏形和箱形基础 4 n 基本假定 ü 变形协调:计算前后基底与地基不脱开 ü 静力平衡:基础在外荷和基底反力作用下满足静力平衡 n 微分方程及其解答 x w (a) O bp dx q x bp M M+dM V (b) q V+dV 4 4 4 w 4 w 0 x d d 4 4 bk EI 1 cos 2 sin 3 cos 4 sin x x w e C x C x e C x C x q 0 n 文克尔(Winkler,1867)假定土体表面任一点压力强度p仅 与该点竖向位移s成正比 p k s k—地基抗力系数或基床系数,kN/m3,可查表1-12及1-13(P.25) 图3.1 文克勒地基上梁的计算 控制 方程 令 通解

3.柱下条形基础、筏形和箱形基础 3.2弹性地基上梁的分析 ■ 梁的分类 √短梁(刚性梁):2Kπ/4; √有限长梁:π/4π 称为柔度指数,为无量纲数 ■分类求解及其解答 √集中荷载下的无限长梁解答 (式3-8) √集中力偶作用下的无限长梁解答 (式3-10) 1 集中力作用下的半无限长梁解答 (式3-11) √力偶作用下的半无限长梁解答 (式3-12) √有限长梁解答 (式3-14) 短梁(刚性梁) 5
3.柱下条形基础、筏形和箱形基础 5 n 梁的分类 ü 短梁(刚性梁) :lp l称为柔度指数,为无量纲数 n 分类求解及其解答 ü 集中荷载下的无限长梁解答 (式3-8) ü 集中力偶作用下的无限长梁解答 (式3-10) ü 集中力作用下的半无限长梁解答 (式3-11) ü 力偶作用下的半无限长梁解答 (式3-12) ü 有限长梁解答 (式3-14) ü 短梁(刚性梁)

3.柱下条形基础、筏形和箱形基础 3.3.1构造要求 翼板厚>200mm,250mm变厚达1.3; 柱荷较大时在柱位处加腋;板宽按地基承载力定 肋梁高由计算确定,初估可取柱距的1/8~1/4,肋宽由截 面抗剪确定 两端宜伸出柱边,外伸悬臂长L,宜为边跨柱距的1/4 肋梁纵向钢筋按计算确定,顶部纵筋通长配置,底部须有 13以上通长配置。当肋梁腹板高≥450mm时,应设腰筋箍 筋按计算确定,做成封闭式,并局部加密。底板受力筋按 计算确定 砼强度等级≥C20,垫层为C10,厚70100mm 6
3.柱下条形基础、筏形和箱形基础 6 n 翼板厚≥200mm,250mm变厚i≤1.3; 柱荷较大时在柱位处加腋;板宽按地基承载力定 n 肋梁高由计算确定,初估可取柱距的1/8~1/4,肋宽由截 面抗剪确定 n 两端宜伸出柱边,外伸悬臂长l0宜为边跨柱距的1/4 n 肋梁纵向钢筋按计算确定,顶部纵筋通长配置,底部须有 1/3以上通长配置。当肋梁腹板高≥450mm时,应设腰筋箍 筋按计算确定,做成封闭式,并局部加密。底板受力筋按 计算确定 n 砼强度等级≥C20,垫层为C10,厚70~100 mm

3.柱下条形基础、筏形和箱形基础 3.3.2柱下条基的计算 ■ 计算内容与方法 √基底尺寸确定:按构造定基长1,按地基承载力定基宽b, 并力使基础形心与荷载重心重合,地基反力均匀分布 √翼板计算:按悬臂板考虑,由抗剪定其厚度,按抗弯配筋 梁纵向内力分析:四种方法 静定分析法 。 做法:假定基底反力线性分布,求基底净反力p,按静力 平衡求任意截面的V及M并绘图,以此进行抗剪计算及配筋。 。 特点:不考虑基础与上部结构相互作用,整体弯曲下所得 截面最大弯矩绝对值一般偏大,故只宜用于上部为柔性结 构、且基础自身刚度较大的条基及联合基础 7
3.柱下条形基础、筏形和箱形基础 7 n 计算内容与方法 ü 基底尺寸确定:按构造定基长l,按地基承载力定基宽b, 并力使基础形心与荷载重心重合,地基反力均匀分布 ü 翼板计算:按悬臂板考虑,由抗剪定其厚度,按抗弯配筋 ü 梁纵向内力分析:四种方法 u 静定分析法 • 做法:假定基底反力线性分布,求基底净反力pj,按静力 平衡求任意截面的V及M并绘图,以此进行抗剪计算及配筋。 • 特点:不考虑基础与上部结构相互作用,整体弯曲下所得 截面最大弯矩绝对值一般偏大,故只宜用于上部为柔性结 构、且基础自身刚度较大的条基及联合基础

3.柱下条形基础、筏形和箱形基础 3.3.2柱下条基的计算 倒梁法 a 前提:刚性梁,基底反力直线分布 按设计要求拟定基础尺寸和荷载; 计算基底净反力分布; 净反力分布图 定计算简图:以柱端为不动铰支的多 基底反力分布 跨连续梁,基底净反力为荷载; (b) ·用弯矩分配法计算弯矩分布,根据支 座弯矩及荷载,以每跨为隔离体求出 支座反力,并绘制剪力分布图; 净反力分布图 调整及消除支座的不平衡力; 按连续梁求内力 叠加逐次计算结果,求最终内力分布 图3.2倒梁法简图8
3.柱下条形基础、筏形和箱形基础 8 • 前提:刚性梁,基底反力直线分布 • 按设计要求拟定基础尺寸和荷载; • 计算基底净反力分布; • 定计算简图:以柱端为不动铰支的多 跨连续梁,基底净反力为荷载; • 用弯矩分配法计算弯矩分布,根据支 座弯矩及荷载,以每跨为隔离体求出 支座反力,并绘制剪力分布图; • 调整及消除支座的不平衡力; • 叠加逐次计算结果,求最终内力分布 F1 M1 F2 M2 F3 M3 F4 M4 pjmaxb pjminb pjmaxb pjminb (a) (b) 净反力分布图 净反力分布图 按连续梁求内力 F1 M1 F2 M2 F3 M3 F4 M4 pjmaxb pjminb pjmaxb pjminb (a) (b) 净反力分布图 净反力分布图 基底反力分布 u 倒梁法 图3.2倒梁法简图

3.柱下条形基础、筏形和箱形基础 3.3.2柱下条基的计算 倒梁法 主要缺点:忽略了梁整体弯曲所产生的内力以及柱脚不均 匀沉降引起上部结构的次应力,误差较大,且偏于不安全 > 存在问题: 。 计算所得反力R,与原荷载N不相等; 。 由于N与σ已知,故按静定结构也可求出内力,且结果与连 续梁不一致; 没有考虑地基土和梁的挠曲变形影响,导致软土偏于危险, 好土过于安全 适用对象:地基比较均匀,上部结构刚度较好,荷载分布 较均匀,且基础梁接近于刚性梁(梁高大于柱距的1/6) 9
3.柱下条形基础、筏形和箱形基础 9 Ø 主要缺点:忽略了梁整体弯曲所产生的内力以及柱脚不均 匀沉降引起上部结构的次应力,误差较大,且偏于不安全 Ø 存在问题: • 计算所得反力Ri与原荷载Ni不相等; • 由于N与σ已知,故按静定结构也可求出内力,且结果与连 续梁不一致; • 没有考虑地基土和梁的挠曲变形影响,导致软土偏于危险, 好土过于安全 Ø 适用对象:地基比较均匀,上部结构刚度较好,荷载分布 较均匀,且基础梁接近于刚性梁(梁高大于柱距的1/6) u 倒梁法

3.柱下条形基础、筏形和箱形基础 3.3.2柱下条基的计算 ◆链杆法一弹性半空间地基上梁的简化计算 >基本思路:将连续支承于地基上的梁简化为用有限个 链杆支承的梁,以阶梯形反力逼近实际反力,再将每 段分布力用集中力代替。将无数支点的超静定问题变 为若干个弹性支座上的连续梁,再用结构力学方法求解。 >主要特点:应用较广,适用于任何荷载及梁断面变化 情况;以阶梯型反力代替连续反力有误差,计算较繁。 10
3.柱下条形基础、筏形和箱形基础 10 u 链杆法—弹性半空间地基上梁的简化计算 Ø 基本思路:将连续支承于地基上的梁简化为用有限个 链杆支承的梁,以阶梯形反力逼近实际反力,再将每 段分布力用集中力代替。将无数支点的超静定问题变 为若干个弹性支座上的连续梁,再用结构力学方法求解。 Ø 主要特点: 应用较广,适用于任何荷载及梁断面变化 情况;以阶梯型反力代替连续反力有误差,计算较繁

3.柱下条形基础、筏形和箱形基础 3.3.2柱下条基的计算 ◆纽马克(Newmark)法一计算弹性地基梁 >计算原理:1943年提出,用于计算挠度、力矩和屈曲荷载, 适用于变截面杆件。假定地基为文克尔地基,地基系数沿 梁的轴线可任意变化,将梁沿轴线分为段,每段土反力 用一系列弹簧代替,弹簧个数为+1,刚度为: k;=kb,l; 4一每段梁长; 地基反力为: P=kiyi 一该段地基沉降 梁 B 室享等室美 k 图3.3用纽马克法计算地基梁简图 11
3.柱下条形基础、筏形和箱形基础 11 u 纽马克(Newmark)法—计算弹性地基梁 Ø 计算原理:1943年提出,用于计算挠度、力矩和屈曲荷载, 适用于变截面杆件。假定地基为文克尔地基,地基系数沿 梁的轴线可任意变化,将梁沿轴线分为n段,每段土反力 用一系列弹簧代替,弹簧个数为n+1,刚度为: li —每段梁长; 地基反力为: yi—该段地基沉降 i i i k kb l i i i P k y 1 2 3 k 1 k 2 ki n+1 k n+1 A 梁 B 图3.3用纽马克法计算地基梁简图