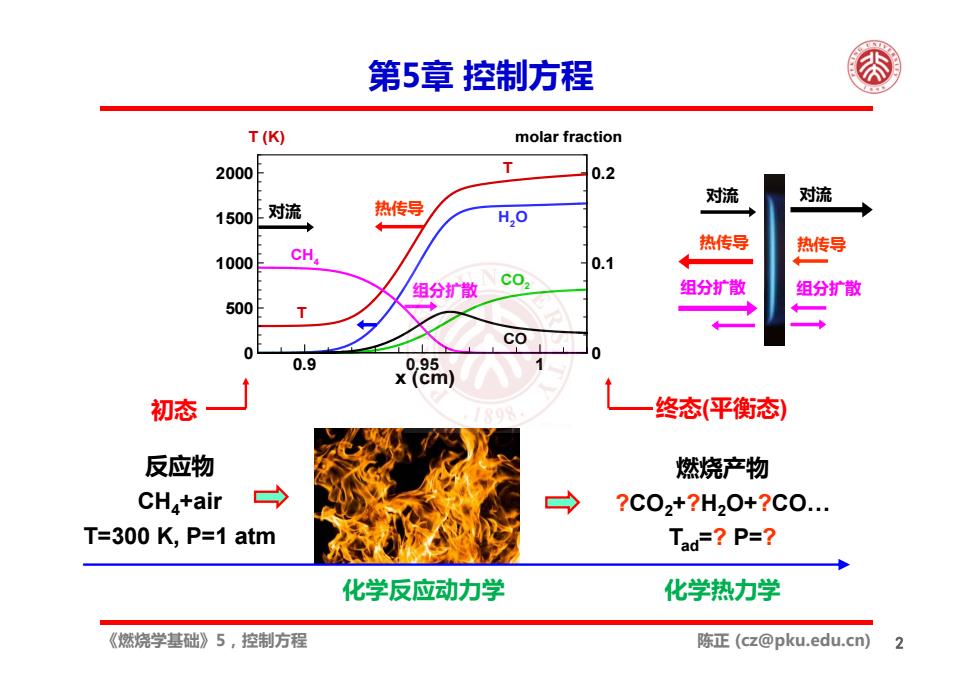
第5章控制方程 T (K) molar fraction 2000 0.2 对流 对流 1500 对流 热传导 H,O 1000 CH 热传导 热传导 0.1 CO. 组分扩散 组分扩散 组分扩散 500 T CO 0 0 0.9 x(cm)1 0.95 初态 终态(平衡态) 反应物 燃烧产物 CH+air → 7C02+?H20+?C0.… T=300 K,P=1 atm Tad=?P=? 化学反应动力学 化学热力学 《燃烧学基础》5,控制方程 陈正(cz@pku.edu.cn) 2
《燃烧学基础》5,控制方程 陈正 (cz@pku.edu.cn) x (cm) 0.9 0.95 1 0 500 1000 1500 2000 0 0.1 0.2 CH4 CO2 H2O CO T (K) T T molar fraction 第5章 控制方程 2 初态 终态(平衡态) 反应物 CH4+air T=300 K, P=1 atm 燃烧产物 ?CO2+?H2O+?CO… Tad=? P=? 化学反应动力学 化学热力学 热传导 组分扩散 对流 对流 对流 热传导 组分扩散 热传导 组分扩散
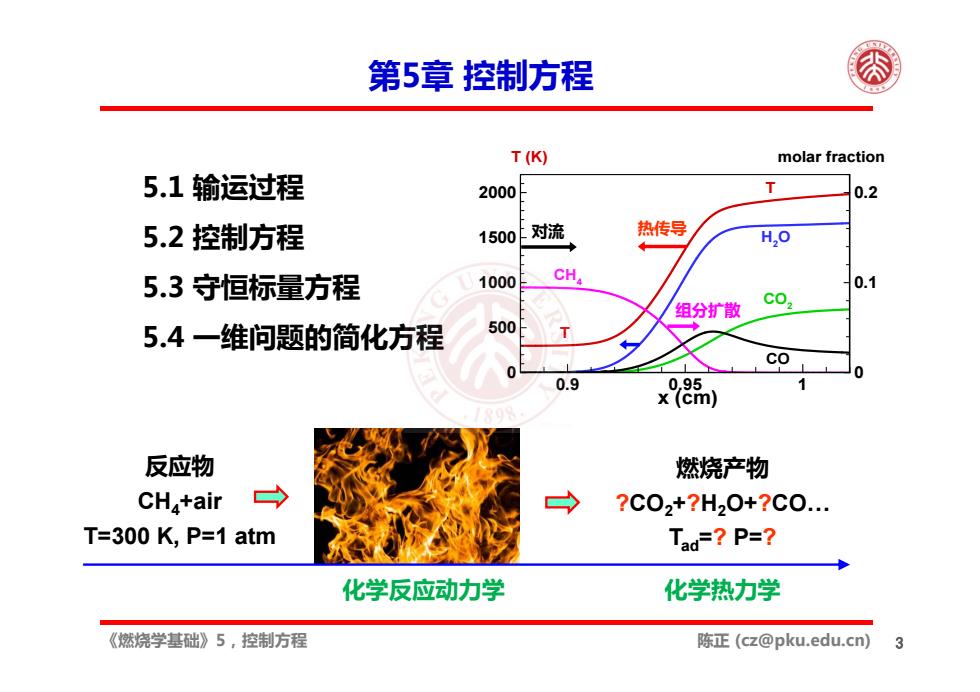
第5章控制方程 T(K) molar fraction 5.1输运过程 2000日 T 0.2 5.2控制方程 1500对流 热传导 H,O 5.3守恒标量方程 1000 CHa 0.1 组分扩散 cO, 5.4一维问题的简化方程 500 co 0 0.9 0.95 x (cm) 反应物 燃烧产物 CH+air ?C02+?H20+?C0. T=300 K,P=1 atm Tad=?P=? 化学反应动力学 化学热力学 《燃烧学基础》5,控制方程 陈正(cz@pku.edu.cn) 3
《燃烧学基础》5,控制方程 陈正 (cz@pku.edu.cn) 第5章 控制方程 3 反应物 CH4+air T=300 K, P=1 atm 燃烧产物 ?CO2+?H2O+?CO… Tad=? P=? 化学反应动力学 化学热力学 5.1 输运过程 5.2 控制方程 5.3 守恒标量方程 5.4 一维问题的简化方程 x (cm) 0.9 0.95 1 0 500 1000 1500 2000 0 0.1 0.2 CH4 CO2 H2O CO T (K) T T molar fraction 热传导 组分扩散 对流
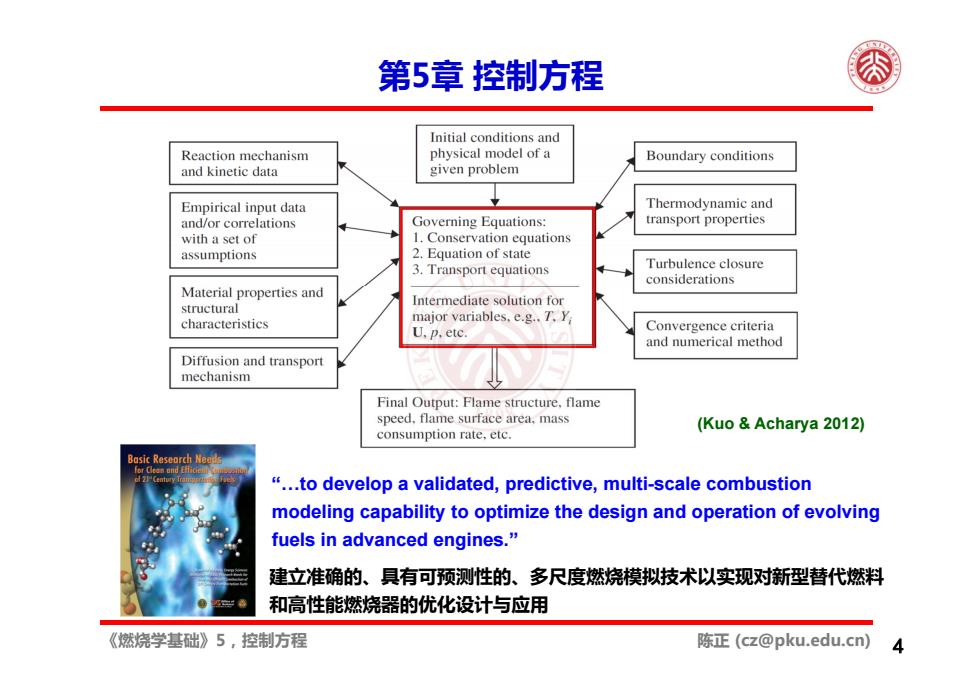
第5章控制方程 Initial conditions and Reaction mechanism physical model of a Boundary conditions and kinetic data given problem Empirical input data Thermodynamic and and/or correlations Governing Equations: transport properties with a set of 1.Conservation equations assumptions 2.Equation of state 3.Transport equations Turbulence closure considerations Material properties and structural Intermediate solution for major variables.e.g..7.Y characteristics U.p.etc. Convergence criteria and numerical method Diffusion and transport mechanism Final Output:Flame structure,flame speed.flame surface area,mass (Kuo Acharya 2012) consumption rate,etc. "...to develop a validated,predictive,multi-scale combustion modeling capability to optimize the design and operation of evolving fuels in advanced engines." 建立准确的、具有可预测性的、多尺度燃烧模拟技术以实现对新型替代燃料 和高性能燃烧器的优化设计与应用 《燃烧学基础》5,控制方程 陈正(cz@pku.edu.cn)
《燃烧学基础》5,控制方程 陈正 (cz@pku.edu.cn) 第5章 控制方程 4 (Kuo & Acharya 2012) “…to develop a validated, predictive, multi-scale combustion modeling capability to optimize the design and operation of evolving fuels in advanced engines.” 建立准确的、具有可预测性的、多尺度燃烧模拟技术以实现对新型替代燃料 和高性能燃烧器的优化设计与应用

输运过程 ■ 输运现象指由于分子的随机热运动而导致宏观状态量(速度、温度、浓度 等)的空间分布发生变化。 Region 1 Region 2 C1>C2 C. 高浓度 → 低浓度 (Figure from internet) 《燃烧学基础》5,控制方程 陈正(cz@pku.edu.cn】 5
《燃烧学基础》5,控制方程 陈正 (cz@pku.edu.cn) 输运过程 5 输运现象指由于分子的随机热运动而导致宏观状态量(速度、温度、浓度 等)的空间分布发生变化。 C1 > C2 高浓度 低浓度 (Figure from internet)

输运过程 ■输运现象指由于分子的随机热运动而导致宏观状态量(速度、温度、浓度 等)的空间分布发生变化。 T1>T2 ■热传导 ■热对流 口自然对流 口强迫对流 ■热辐射 高温 → 低温 (Figure from internet) 《燃烧学基础》5,控制方程 陈正(cz@pku.edu.cn) 6
《燃烧学基础》5,控制方程 陈正 (cz@pku.edu.cn) 输运过程 6 输运现象指由于分子的随机热运动而导致宏观状态量(速度、温度、浓度 等)的空间分布发生变化。 T1 > T2 高温 低温 (Figure from internet) T1 T2 热传导 热对流 自然对流 强迫对流 热辐射

输运过程 ■输运现象指由于分子的随机热运动而导致宏观状态量(速度、温度、浓度 等)的空间分布发生变化。 宏观原因 分子输运 宏观体现 流速空间分布不均匀 动量 粘性:t=d,/dc 温度空间分布不均匀 能量 热传导:q=-dT1c, 组分浓度空间分布不均匀 组分质量 质量扩散:4=-pD,d4/在2 898 wwwzuzwuuluuuuauau 动量 Direction of 热量 Direction of 组分 Direction of momentum transfer I heat conduction CA diffusion B wmnn. Cp Va>VB TA>TE 91>8 《燃烧学基础》5,控制方程 陈正(cz@pku.edu.cn)
《燃烧学基础》5,控制方程 陈正 (cz@pku.edu.cn) 输运过程 7 输运现象指由于分子的随机热运动而导致宏观状态量(速度、温度、浓度 等)的空间分布发生变化。 动量 热量 组分 宏观原因 分子输运 宏观体现 流速空间分布不均匀 温度空间分布不均匀 组分浓度空间分布不均匀 动量 能量 组分质量 粘性: 热传导: 质量扩散: 21 / dxdu 2 / dxdTq 2 A AA / dxdYD

输运过程 ■输运现象指由于分子的随机热运动而导致宏观状态量(速度、温度、浓度 等)的空间分布发生变化。 宏观原因 分子输运 宏观体现 流速空间分布不均匀 动量 粘性:x=μd,/dc 温度空间分布不均匀 能量 热传导:q=-dT/c, 组分浓度空间分布不均匀 组分质量 质量扩散:T4=-pD,dY4/d2 nq A 运动板 高温板☑ 高浓度☑ u1=u1(X2) T=T(X2) YA=YA(X2) X21 X2t X2t 固定板 低温板 低浓度☑ A Newton粘性定律 Fourier热传导定律 Fick扩散定律 udu dx, q=-AdT/dxz T=-pD dy/dx 8
《燃烧学基础》5,控制方程 陈正 (cz@pku.edu.cn) 输运过程 8 输运现象指由于分子的随机热运动而导致宏观状态量(速度、温度、浓度 等)的空间分布发生变化。 运动板 固定板 x2 x1 u1=u1(x2) τ 高温板 低温板 x2 x1 T=T(x2) q q Newton粘性定律 Fourier热传导定律 Fick扩散定律 高浓度 低浓度 x2 x1 YA=YA(x2) ΓA ΓA 21 / dxdu 2 / dxdTq 2 A AA / dxdYD 宏观原因 分子输运 宏观体现 流速空间分布不均匀 温度空间分布不均匀 组分浓度空间分布不均匀 动量 能量 组分质量 粘性: 热传导: 质量扩散: 21 / dxdu 2 / dxdTq 2 A AA / dxdYD

Newton粘性定律 两个无限宽和无限长的不可渗透的平板,它们相距⊙距离, 中间充满等温的流体B。坐标及位置如图3-1所示。如果下平板 运动板立乙 图3-1牛顿粘性定体 囿定不动,上平板以定常速度4…运动,由实验发现,流体的速 度由上平板处的4变到下平板处的零。这表明流速快的一层和 流速慢的-一层之间有剪切力。流速慢的一层对流速快的一层有阻 力。单位面积上剪切力的大小和速度梯度4/y成正比。即: e一影 (3-21) 这就是牛顿粘性定律。T是单位面积上的剪切力,“是动力粘性 系数(也称动力粘度),/y是速度梯度。也称剪切速率,负 号表示动量传递与速度4增加的方向相反。 (来自傅维镳《燃烧学》) 《燃烧学基础》5,控制方程 陈正(cz@pku.edu.cn】 9
《燃烧学基础》5,控制方程 陈正 (cz@pku.edu.cn) Newton粘性定律 9 ( 来自傅维镳《燃烧学》)

Fourier热传导定律 在湘距·的两个平行平板之间,充满一种静止流体,上板温 度为T,下板温度为T,且T>T。(图3-2)。因沿y方向上 热板2227222Z2227Z7 冷板☑ 因3-2德立时导热定排 各层之间的温度不同,由于温差,各层之间产生了热量交换。热 量将从温度高的一层流向温度低的一层。单位时间内,单位面积 上的热流量是与温度梯度成正比的,即: 9=-元 (3-23) dy 这就是傅立叶导热定律。9是单位时间单位面积上的热流盘,入是 导热系数,江⊙y是温度梯度,负号表示热流方向与温度增加的 方向相反。 (来自傅维镳《燃烧学》) 《燃烧学基础》5,控制方程 陈n正(cz@pku.edu.cn 10
《燃烧学基础》5,控制方程 陈正 (cz@pku.edu.cn) Fourier热传导定律 10 ( 来自傅维镳《燃烧学》)

Fick扩散定律 在相距为6的两个多孔的平行平板之间,充满一种静止的等 温流体B。另一种与B温度相同的流体A从一边渗入(渗入浓度 为CA),而从另一边渗出(渗出浓度为CAw)。而且CA>CAw, 横坐标代表A的浓度。这样在日中不同的层上,A的浓度不同。 由于浓度差存在,而产生扩散。单位时间、单位面积上流体A护 散造成的物质流与在B中流体A的浓度梯度成正比,即: =盼 (3-25) 这就是费克扩散定律。J。表示单位时间内,单位面积上流体A 扩散造成的物质流量,DaB是A在B中的扩散系数。aP/y是 浓度梯度,负号表示扩散物质流的方问与浓度增加的方向相反。 CA 图3-3费克扩散定 (来自傅维镳《燃烧学》) 《燃烧学基础》5,控制方程 陈正(cz@pku.edu.cn) 11
《燃烧学基础》5,控制方程 陈正 (cz@pku.edu.cn) Fick扩散定律 11 ( 来自傅维镳《燃烧学》)