
Lecture 4 Sampling for Big Data
Lecture 4 Sampling for Big Data
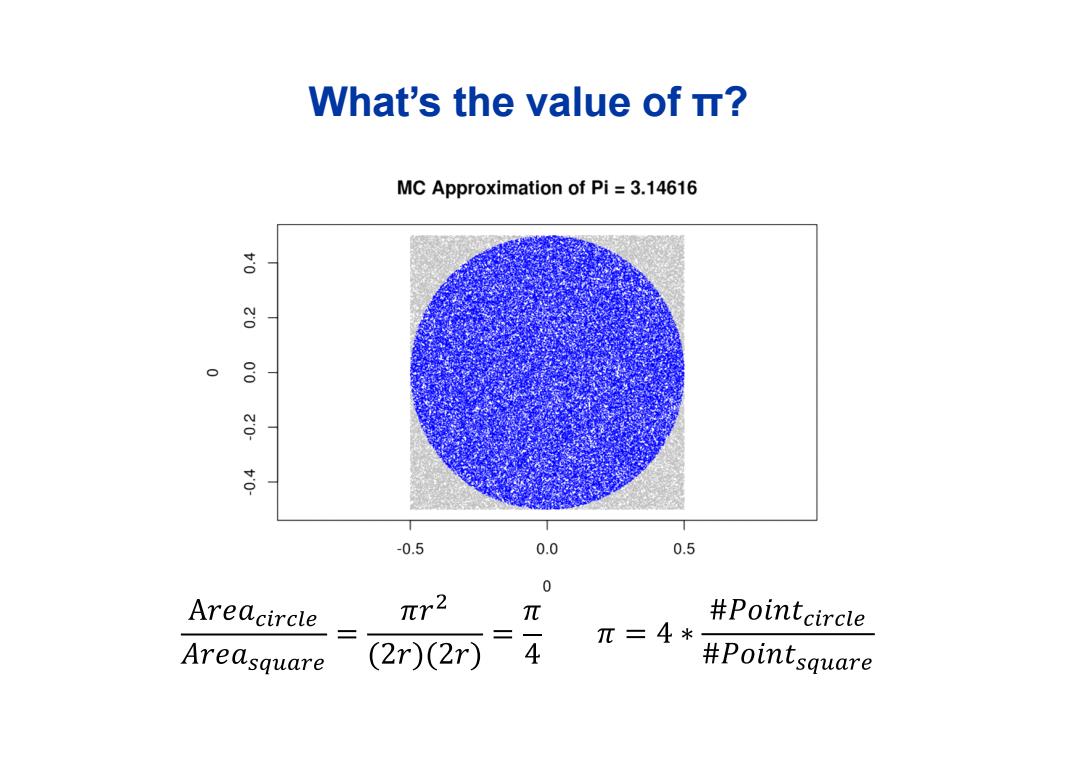
What's the value of TT? MC Approximation of Pi 3.14616 8 -0.5 0.0 0.5 0 Areacircle πr2 π #Pointcircle π=4* Areasquare (2r)(2r) =4 #Pointsquare
What’s the value of π?
Outline >Motivation /Benefits >Basics of sampling Inverse Transform sampling ·Rejection sampling ·Importance sampling Markov chain Monte Carlo (MCMC) MH Sampling Gibbs Sampling >Stream sampling Sample >Conclusion
¾Motivation / Benefits ¾Basics of sampling • Inverse Transform sampling • Rejection sampling • Importance sampling • Markov chain Monte Carlo (MCMC) MH Sampling Gibbs Sampling ¾Stream sampling ¾Conclusion Outline
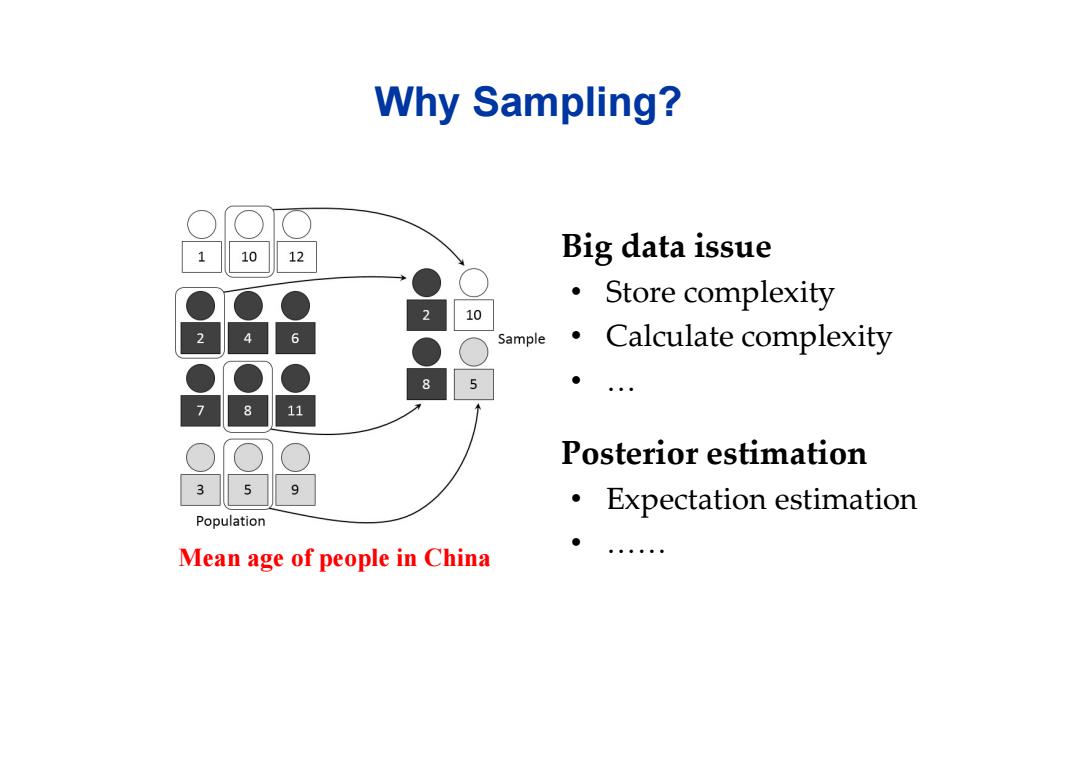
Why Sampling? 10 12 Big data issue 。 Store complexity 2 10 Sample Calculate complexity 35 ● Posterior estimation Expectation estimation Population ● Mean age of people in China
Big data issue • Store complexity • Calculate complexity • … Why Sampling? Posterior estimation • Expectation estimation • …… Mean age of people in China

Bad Sampling Perform your research with bad samples,or just ones that are inaccurately designed,and you will almost certainly get misleading results. Examples:only sample teenagers when querying the mean age of people in China YOUR SAMPLING IS BAD AND YOU SHOULD FEEL BAD
Bad Sampling • Perform your research with bad samples, or just ones that are inaccurately designed, and you will almost certainly get misleading results. • Examples: only sample teenagers when querying the mean age of people in China
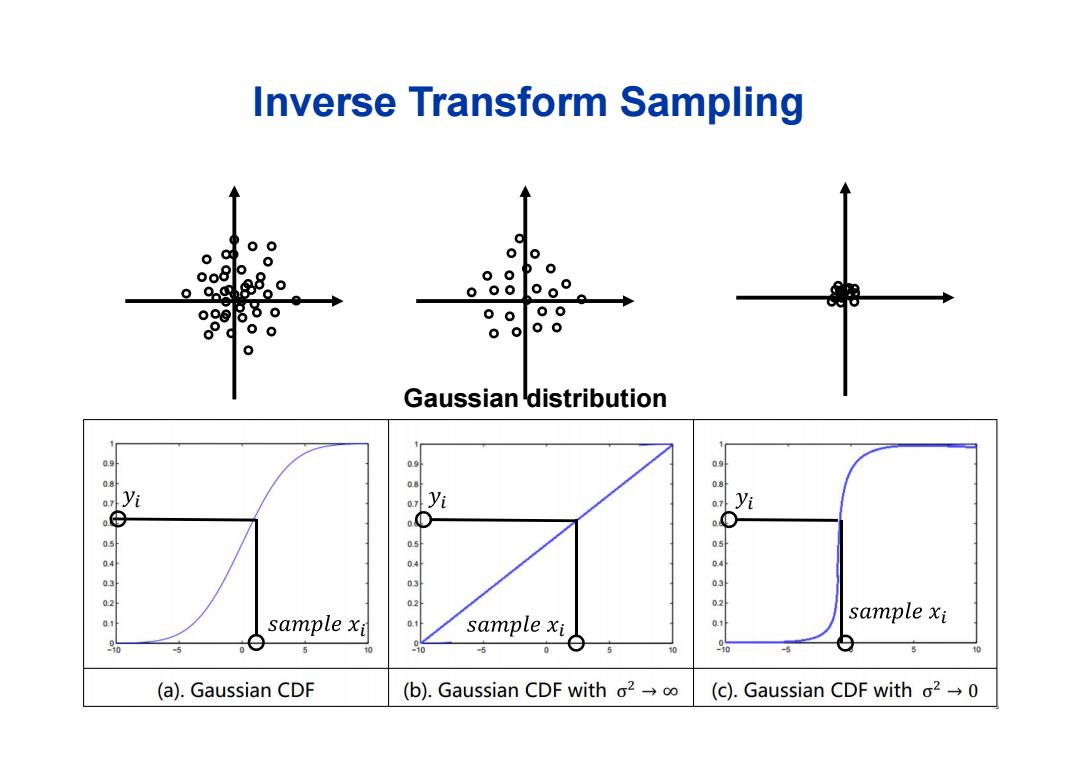
Inverse Transform Sampling 00 9 Qo 6 0 P 9 9.0 000 o。0 08 88o 00 00 0 oo 00 Gaussian distribution 0.9 Q.8 yi ® 03 02 0.2 0.1 sample xi sample xi 01 sample xi 90 5 0 10 5 (a).Gaussian CDF (b).Gaussian CDF with o2o (c).Gaussian CDF with o20
Gaussian distribution Inverse Transform Sampling

Inverse Transform Sampling >Sampling based on the inverse of Cumulative Distribution Function(CDF) >Method: CDF Sampling: Yi~Uniform(0,1) Xi=CDF-1(Yi) >Drawbacks: Usually,it's hard to get the inverse function
¾Sampling based on the inverse of Cumulative Distribution Function (CDF) ¾Method: ¾Drawbacks: • Usually, it’s hard to get the inverse function Inverse Transform Sampling
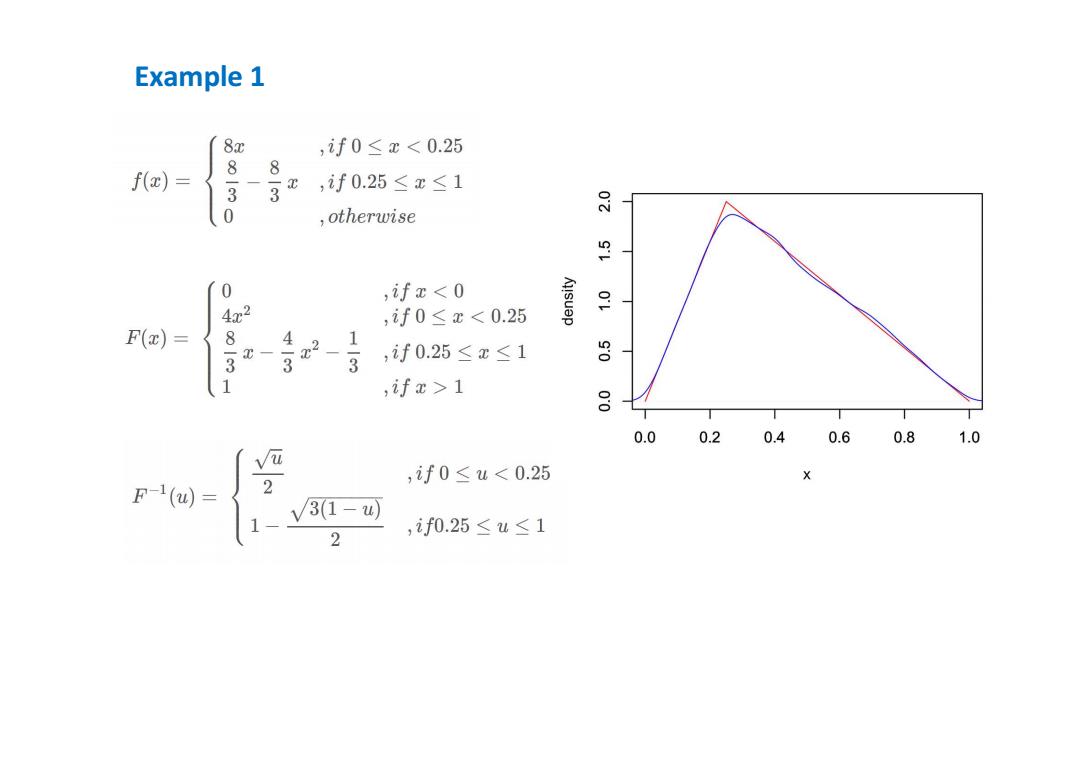
Example 1 8x ,if0≤x1 8 0.0 0.2 0.4 0.6 0.8 1.0 ,if0≤u<0.25 V31- ,if0.25≤u≤1 2
Example 1
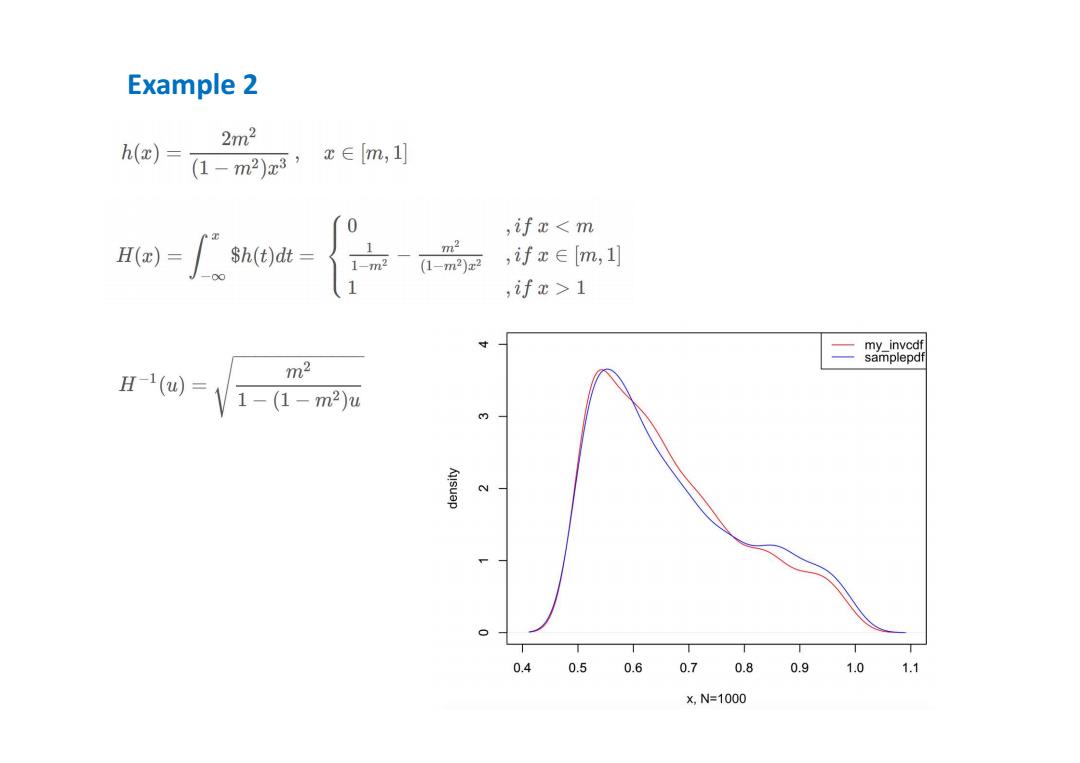
Example 2 2m2 h(x)= (1-m2)z8, x∈m, '0 ,ifx1 my_invcdf samplepdf m2 H1(w=√1-(1-m2u 0.4 0.50.6 0.7 0.8 0.91.0 1.1 x,N=1000
Example 2

Rejection Sampling Ideas: Accept the samples in the region under the graph of its density function and reject others Rejection Sampling: Proposal distribution Q(x) Xi~Q(X) reject a~Uniform(0,Q(Xi)) Mq(x) if(a≤P(X) accept Accept p(x) else Reject x(i) Acceptance ratio =p(x)/Mg(x)
Ideas: • Accept the samples in the region under the graph of its density function and reject others Proposal distribution Q(x) Rejection Sampling Acceptance ratio = p(x)/Mq(x)