
第五章搜索策略 §5.1基本概念 1什么是搜索 ()搜索引起:人工智能要解决的问题大部分 是结构不良或非结构化的问题,而对这样的 问题一般不存在成熟的的求解算法,只能用 已有的知识一步步地摸索着前进 (2)搜索:根据问题的实际情况不断寻找可利 用的知识,从而构造一条代价较少的推理路 线,使问题得到圆满解决的过程。 (3)搜索分为〔盲目搜索 启发式搜索(好)
第五章 搜索策略 §5.1 基本概念 1 什么是搜索 (1)搜索引起:人工智能要解决的问题大部分 是结构不良或非结构化的问题,而对这样的 问题一般不存在成熟的的求解算法,只能用 已有的知识一步步地摸索着前进 (2)搜索:根据问题的实际情况不断寻找可利 用的知识,从而构造一条代价较少的推理路 线,使问题得到圆满解决的过程。 (3)搜索分为 盲目搜索 启发式搜索(好)

·盲目搜索:是按预定的控制策略进行搜索 在搜索的过程获得的中间信息不用来改进控 制策略,搜索具有盲目性,效率不高,不便 于复杂问题的求解 ·启发式搜索:在搜索中加入了与问题有关的 启发式信息,用于指导搜索朝着最有希望的 方向前进,加速问题的求解过程并找到最优 解 2状态空间表示法 ·状态空间表示法是由《状态”和《算符》来 表示问题的一种方法。“状态”用以描述问 题求解过程中不同时刻的状况;“算符”表 示对状态的操作,算符的每一次使用就使问 题由一种状态变换为另一种状态
• 盲目搜索:是按预定的控制策略进行搜索, 在搜索的过程获得的中间信息不用来改进控 制策略,搜索具有盲目性,效率不高,不便 于复杂问题的求解 • 启发式搜索:在搜索中加入了与问题有关的 启发式信息,用于指导搜索朝着最有希望的 方向前进,加速问题的求解过程并找到最优 解 2 状态空间表示法 • 状态空间表示法是由“状态”和“算符”来 表示问题的一种方法。 “状态”用以描述问 题求解过程中不同时刻的状况;“算符”表 示对状态的操作,算符的每一次使用就使问 题由一种状态变换为另一种状态

(1)状态:描迷问题求解过程中任一时刻状况的数据 结构,一般用一组变量的有序组合表示: Sk=(Sko,Sk1...) 当每一个分量确定时,就得到一个具体的状态 (2)算符:引起状态中某些分量发生变化,从而使问 题由一个状态变为另一个状态的操作称为算符 (③)状态空间:由问题的全部状态及一切可用算符所 构成的集合称为问题的状态空间,一般用一个三元 组表示(S,F,G) 初始状态集合算符集合目标状态集合 (4)状态空间的图示形式称为状态空间图,节点表示 状态,有向边(弧)表示算符
(1)状态:描述问题求解过程中任一时刻状况的数据 结构,一般用一组变量的有序组合表示: Sk=(Sk0,Sk1…) 当每一个分量确定时,就得到一个具体的状态 (2)算符:引起状态中某些分量发生变化,从而使问 题由一个状态变为另一个状态的操作称为算符 (3)状态空间:由问题的全部状态及一切可用算符所 构成的集合称为问题的状态空间,一般用一个三元 组表示(S,F,G) 初始状态集合 算符集合 目标状态集合 (4)状态空间的图示形式称为状态空间图,节点表示 状态,有向边(弧)表示算符
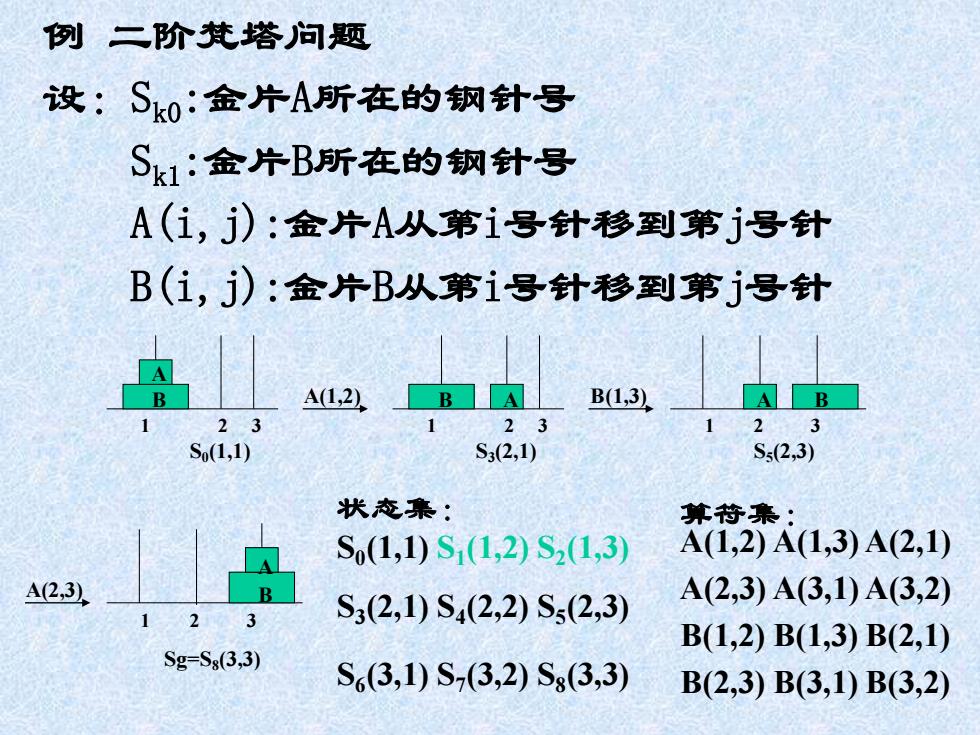
例二阶梵塔问题 设:Sk0:金片A所在的钢针号 Sk1:金片B所在的钢针号 A(1,j):金片A从第1号针移到第j号针 B(1,j):金片B从第1号针移到第j号针 42 B(1,3 23 23 23 So(1,1) S3(2,1) Ss(2,3) 状态集: 算符集: So(1,1)S1(1,2)S2(1,3) A(1,2)A(1,3)A(2,1) A2,3 2 S3(2,1)S42,2)Ss(2,3) A(2,3)A(3,1)A(3,2) B(1,2)B(1,3)B(2,1) Sg=Ss(3,3) S6(3,1)S73,2)Sg3,3) B(2,3)B(3,1)B(3,2)
例 二阶梵塔问题 设:Sk0:金片A所在的钢针号 Sk1:金片B所在的钢针号 A(i,j):金片A从第i号针移到第j号针 B(i,j):金片B从第i号针移到第j号针 A B 1 2 3 S0 (1,1) A(1,2) B 1 2 3 S5 (2,3) A B(1,3) A B 1 2 3 S3 (2,1) 1 2 3 Sg=S8 (3,3) A(2,3) B A 状态集: S0 (1,1) S1 (1,2) S2 (1,3) S3 (2,1) S4 (2,2) S5 (2,3) S6 (3,1) S7 (3,2) S8 (3,3) 算符集: A(1,2) A(1,3) A(2,1) A(2,3) A(3,1) A(3,2) B(1,2) B(1,3) B(2,1) B(2,3) B(3,1) B(3,2)
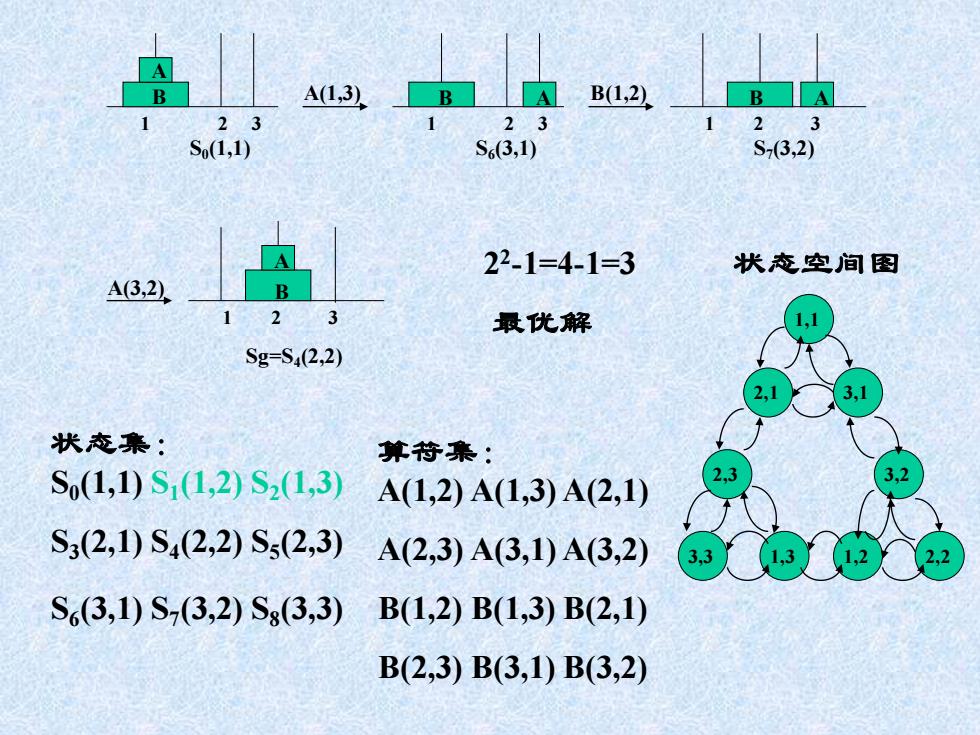
B B(1,2 23 203 2 So(1,1) S6(3,1) S73,2) 22-1=4-1=3 状态空间图 A3,2 23 最优解 Sg=S4(2,2) 状态集: 算符集: S(1,1)S1(1,2)S2(1,3) 23 3,2 A(1,2)A(1,3)A(2,1) S3(2,1)S4(2,2)Ss(2,3) A(2,3)A(3,1)A(3,2) 3,3 1222 S63,1)S73,2)Sg(3,3)B(1,2)B(1,3)B(2,1) B(2,3)B(3,1)B(3,2)
A B 1 2 3 S0 (1,1) A(1,3) B 1 2 3 S7 (3,2) A B(1,2) B A 1 2 3 S6 (3,1) 1 2 3 Sg=S4 (2,2) A(3,2) B A 2 2 -1=4-1=3 状态空间图 最优解 状态集: S0 (1,1) S1 (1,2) S2 (1,3) S3 (2,1) S4 (2,2) S5 (2,3) S6 (3,1) S7 (3,2) S8 (3,3) 算符集: A(1,2) A(1,3) A(2,1) A(2,3) A(3,1) A(3,2) B(1,2) B(1,3) B(2,1) B(2,3) B(3,1) B(3,2) 1,1 2,1 2,3 3,3 1,3 1,2 2,2 3,1 3,2

(⑤)解题过程 ·定义状态描述,定义一组算符 ·问题的求解过程是一个不断把算符作用于 状态的过程 ·算符的一次使用,就使问题由一种状态转 变为另一种状态,使用算符最少的解称为 最优解 ·对任何一个状态,可使用的算符不止一个, 生成的后继状态可能有多个,涉及搜索策 略
(5)解题过程 • 定义状态描述,定义一组算符 • 问题的求解过程是一个不断把算符作用于 状态的过程 • 算符的一次使用,就使问题由一种状态转 变为另一种状态,使用算符最少的解称为 最优解 • 对任何一个状态,可使用的算符不止一个, 生成的后继状态可能有多个,涉及搜索策 略

3与/或树表示法:用于比校复杂的问题 (1)分解:问题分解为子问题,子问题分解为子问题 例P分解成P1,P2,P3三个子问题,只有当这三个 子问题都可以解时,问题P才可解。P1,P2,P3之 间存在“与”关系,节点P为与节点,用一条弧连 接。 (2)等价变换:对于复杂的问题,还可利用同构或 同态的等价变换,把它变换为若干个较容易求 解的新问题。若新问题中有一个可求解,则原 问题可解。 例P被等价变换为三个新问题P1,P2,P3,任何 一个P1可解,P可解,则P1,P2,P3之间存在或关 系,节点P称为或节点。 将上迷两种方法结合使用,称为“与/或
3 与/或树表示法:用于比较复杂的问题 (1)分解:问题分解为子问题,子问题分解为子问题。 例 P分解成P1,P2,P3三个子问题,只有当这三个 子问题都可以解时,问题P才可解。P1,P2,P3之 间存在“与”关系,节点P为与节点,用一条弧连 接。 (2)等价变换:对于复杂的问题,还可利用同构或 同态的等价变换,把它变换为若干个较容易求 解的新问题。若新问题中有一个可求解,则原 问题可解。 例 P被等价变换为三个新问题P1,P2,P3 ,任何 一个Pi可解,P可解,则P1,P2,P3之间存在或关 系,节点P称为或节点。 将上述两种方法结合使用,称为“与/或” 树
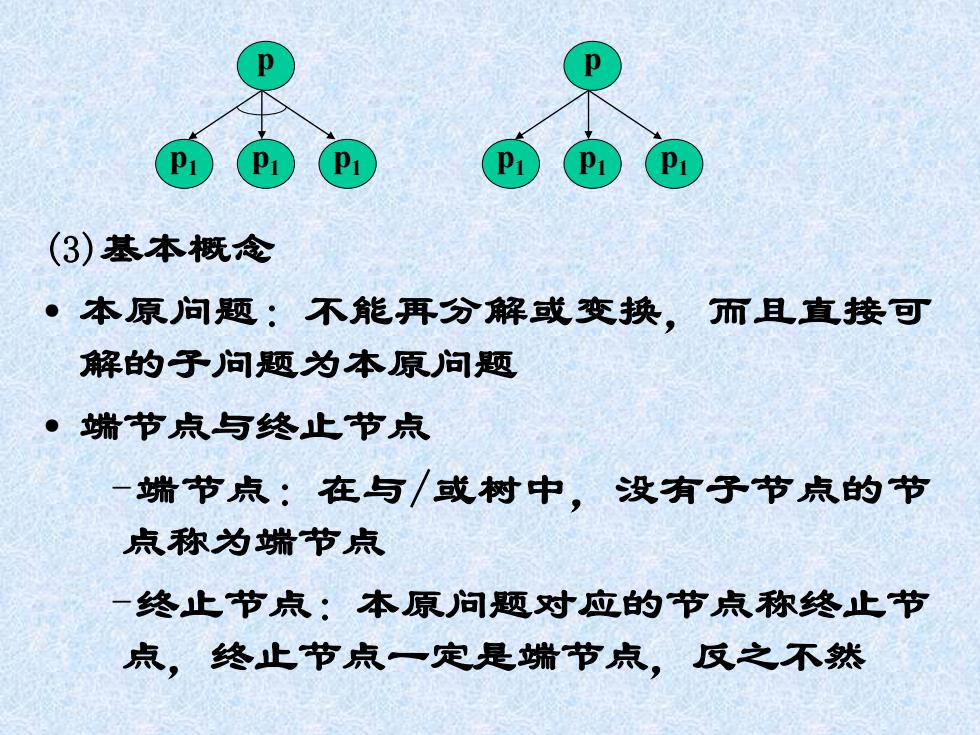
(3)基本概念 ·本原问题:不能再分解或变换,而且直接可 解的子问题为本原问题 ·端节点与终止节点 一端节点:在与或树中,没有子节点的节 点称为端节点 一终止节点:本原问题对应的节点称终止节 点,终止节点一定是蜡节点,反之不然
(3)基本概念 • 本原问题:不能再分解或变换,而且直接可 解的子问题为本原问题 • 端节点与终止节点 –端节点:在与/或树中,没有子节点的节 点称为端节点 –终止节点:本原问题对应的节点称终止节 点,终止节点一定是端节点,反之不然 p p1 p1 p1 p p1 p1 p1

·可解节点:满足下列条件之一 它是一个终止节点 它是一个“或”节点,且子 节点中至少有一个可解节点 -它是一个“与”节点,且子 节点全部是可解节点 ·不可解节点:关于可解节点的 三个条件全部不满足的节点称 为不可解节点 ·解树:由可解节点构成,并且 由这些可解节点推出初始节点 (原始问题)为可解节点的子 树称为解树,解树中一定包含 初始节点
• 可解节点:满足下列条件之一 –它是一个终止节点 –它是一个“或”节点,且子 节点中至少有一个可解节点 –它是一个“与”节点,且子 节点全部是可解节点 • 不可解节点:关于可解节点的 三个条件全部不满足的节点称 为不可解节点 • 解树:由可解节点构成,并且 由这些可解节点推出初始节点 (原始问题)为可解节点的子 树称为解树,解树中一定包含 初始节点。 p t t t t t t t

例三阶梵塔问题 初始状态:三片金片都在1号针上 目标状态:三片金片都在3号针上 要求:小片在大片之上 分析:原问题由三个子问题 1把金片A及B移到2号针的双金片问题一分解3个子 问题 2把金片C移到3号针的单金片问题 3把金片A及B移到3号针的双金片问题一分解3个子 问题 设三元组(i,j,k) 金片C针号 金片B针号 金片A针号
例 三阶梵塔问题 初始状态:三片金片都在1号针上 目标状态:三片金片都在3号针上 要求:小片在大片之上 分析:原问题由三个子问题 1 把金片A及B移到2号针的双金片问题—分解3个子 问题 2 把金片C移到3号针的单金片问题 3 把金片A及B移到3号针的双金片问题—分解3个子 问题 设 三元组(i,j,k) 金片C针号 金片B针号 金片A针号