
试卷代号:1002 座位☐ 中央广播电视大学2009一2010学年度第一学期“开放本科”期末考试(半开卷)》 计算机数学基础(1)试题 2010年1月 题 号 二 三 四 总 分 分 数 得分 评卷人 一、单项选择题(每小题4分,共20分) 1.谓词公式VxA(x)→B与3x(A(x)→B)是(). A.蕴含式 B.重言蕴含式 C.等值式 D.前束范式 2.设集合A={2,{1},则P(A)=(). A.{0,{2},{1} B.{0,{2},{1},{2,1)} C.{2},{1)},{2,{2})} D.{0,{2},{1},{2},{1}}} 3.设集合A={a,b,c,d},B={1,2,3},下列二元关系中是A→B的函数的为( A.R1={(a,1),b,1),(a,2),(d,3)} B.R1={(a,1),(b,2),(c,3)} C.R1={(a,1),(b,2〉,(c,3),a,3)} D.R1={a,1),(b,1),c,2),(d,2)》 4.设L是n阶无向图G上的一条通路,则下面命题为假的是(). A.L可以不是简单通路,而是初级通路 B.L可以既是简单通路,又是初级通路 C.L可以既不是简单通路,又不是初级通路 D.L可以是简单通路,而不是初级通路 7
试卷代号 :1002 座位号口口 中央广播电视大学2009-2010学年度第一学期“开放本科”期末考试(半开卷) 计算机数学基础(1) 试题 2010年 1月 题 号 四 总 分 分 数 得 分 评卷人 一、单项选择题【每小题 4分 ,共 20分) 1.谓词公式 V xA(x)-B与 3 x(A(x)-B)是( ). A.蕴含式 B.重言蕴含式 C.等值式 D.前束范式 2.设集合 A= (2, (1)},则 P(A)=( ). A.{必 ,(2},{{1}}} B.{必,{2},{{1}},{2,{1}}} C.{{2},{{1}},(2,(2}}} D.{必,{2},{{1}},{{2},{{1}}}} 3.设集合 A=(a,b,c,d) ,B=(1,2,3},下列二元关系中是 A-B的函数的为( A. R,={(a,1>,(b,1>,(a,2>,(d,3>} B. R,={(a,1>,(b,2),(C,3)} C. R,={la,1),(b,2),(。,3),(a,3>} D. R,={(a,1>,(b,1),(c,2>,(d,2)} 4.设 L是n阶无向图c上的一条通路,则下面命题为假的是( ). A. L可以不是简单通路,而是初级通路 B. L可以既是简单通路 ,又是初级通路 C. L可以既不是简单通路 ,又不是初级通路 D. L可以是简单通路,而不是初级通路

5.下列结论不正确是(). A.无向连通图G是欧拉图的充分必要条件是G不含奇数度结点 B.无向连通图G有欧拉通路的充分必要条件是G最多有两个奇数度结点 C.有向连通图D是欧拉图的充分必要条件是D的每个结点的入度等于出度 D.有向连通图D是欧拉图的充分必要条件是除两个结点外,每个结点的人度等于 出度 得分 评卷人 二、填空题(每小题4分,共20分) 6.命题公式一(P→Q)的主析取范式为 7.设个体域D={a,b,c},公式YxF(x)→3yG(y)消去量词化为 8.设集合A={a,b,c},集合A上的二元关系R={,,},S= {,},则R·S={ 9.设集合A={1,2},B={a,b},那么集合A到B的双射函数是 10.设图G如图1所示,则图G的割点 图1 得分 评卷人 三、化简计算题(每小题10分,共50分) 11.列命题公式(PVQ)→R的真值表,并给出该公式的成假赋值. 12.设集合A=(a,b,c,d,e},B={b,d,e},C={a,b,d},求(A-B)④(BUC). l3.设二元关系R1={,,,},R2={,, ,},求R1∩R2;R1④R2,Dom(R1),Ran(R2) 8
下列结论不正确是( ). A.无向连通图G是欧拉图的充分必要条件是G不含奇数度结点 B.无向连通图一G有欧拉通路的充分必要条件是G最多有两个奇数度结点 C.有向连通图D是欧拉图的充分必要条件是D的每个结点的人度等于出度 D.有向连通图D是欧拉囱的充分l 案件是除两传点外,每个结点的人度等于 出度 得 分 评卷人 二、懊空题(每小题 4分。共 20分) 命题公式,(P-Q)的主析取范式为 设个体域D = (a,b,c),公式y xF(x)- 3厂勿)消去量词化为 8.设集合A= (a, b, c},集合 A上的二元关系R =(,, , ), S= { ,},则 R·S二 9.设集合A=(1,2),B=(a,b),那么集合 A到B的双射函数是 10.设图G如图 1所示,则图G的割点 ‘得 分 评卷人 三、化简计算题(每小题 10分,共 50分) 11.列命题公式(尸VQ)-}R的真值表,并给出该公式的成假赋值. 12.设集合A= (a,b,c,d,e),B= (b,d, e} ,C= (a,b,d),求(A一B)①(BUC). 13.设二元关系 R,=(,,,),R2=(,, , } 8 ,求 R,门Rz ;R, 0+R2 ,Dom(R,),Ran(R,)

14.设平面图G(如图2) (1)求该平面图有多少个面,并用R。,R1,R2,R,…等标出. (2)写出每个面的边,指出每个面的次数 图2 15.设有向图D=,如图3所示.请回答以下问题: (1)试写出图D的邻接矩阵; 000 0> 0 0001 1102 1102 (2)已知A2(D)= ,A3(D)= 000 0 0 00 000 0 0 00 0 求:从2到v4长度等于3的通路有多少条和顶点处长度小于等于3的回路多少条? 图3 得 分 评卷人 四、证明题(本题共10分】 16.用构造推理方法证明(P→(QVR)∧(S→Q)∧P∧S→R. 9
14.设平面图 G(如图 2) (p求该平面图有多少个面,并用凡:R1 (2)写出每个面的边,指出每个面的次数. R2,R3,…等标出. 15.设有向图D=,如图3所示.请回答以下间题: (1)试写出图D的邻接矩阵; (2)已知 AZ(D) - 0 0 1 0 0 0 0 0 ,A3(D)= 0 0 1 0 0 0 0 0 求:从 v:到 v‘长度等于 3的通路有多少条和顶点 v2处长度小于等于 3的回路多少条? j, 产 ﹄ 门 V . 尸 、 . 3 | V V 得 分 评卷人 四、证明题(本题共 10分) 16.用构造推理方法证明(P- (QVR))A(S-; Q)APASCR
试卷代号:1002 中央广播电视大学2009一2010学年度第一学期“开放本科”期末考试(半开卷) 计算机数学基础(1)试题答案及评分标准 (供参考) 2010年1月 一、单项选择题(每小题4分,共20分) 1.C 2.B 3.D 4.A 5.D 二、填空题(每小题4分,共20分】 6.PΛQ 7.(F(a)∧F(b)∧F(c))→(G(a)VG(b)VG(c) 8.{,,,} 9.f1={,},f2={,} 10.B 三、化简计算题(每小题10分,共50分) 11.做真值表. P Q R PVQ (PVQ)→R 0 0 0 0 1 0 0 1 0 1 0 1 0 1 0 0 1 1 1 1 1 0 0 1 0 1 0 1 1 1 1 0 1 0 1 1 1 1 1 (7分) 公式为假的赋值是(0,1,0),(1,0,0),(1,1,0) (10分) 12.(A-B)D(BUC)=((a,b,c,d,e)-ib,d,e})((b,d,e}U(a,b,d)) ={a,c}①{a,b,d,e} (4分) ={a,b,c,d,e}-{a (8分) ={b,c,d,e} (10分) 10
试卷代号 :1002 中央广播电视大学2009-2010学年度第一学期“开放本科”期末考试(半开卷) 计算机数学基础(1) 试题答案及评分标准 (供参考) 2010年 1月 一、单项选择题(每小题 4分.共 20分 ) 1. C 2. B 3. D 4. A 二、填空题(每小题 4分 ,共 20分) 6. PA ,Q 7. (F(a) A F(b)八F(c))- (G(a) V G(b) V G(c)) 8.{ ,,,} 9. f,={ , }+f2={ , } 10. B 三、化简计算题 (每小题 10分,共 50分 ) 11.做真值表. 5. D 尸 Q R PVQ (P V Q)-R 0 0 0 0 1 0 0 1 0 1 0 1 0 1 0 0 1 1 1 1 1 0 0 1 0 1 0 1 1 1 1 1 0 1 0 1 1 1 1 1 公式为假的赋值是(0,1,0),(1,0,0),(1,1,0). 12. (A一B)0(B U C)=((a,b,c,d,e}一{b,d,e))(D((b,d,e) U(a,b,d}) =(a,。}① (a,b,d,。} =(a,b,c,d,。}一{a) =(b,c,d,e} (7分) (10分) (4分) (8分) (10分) 10
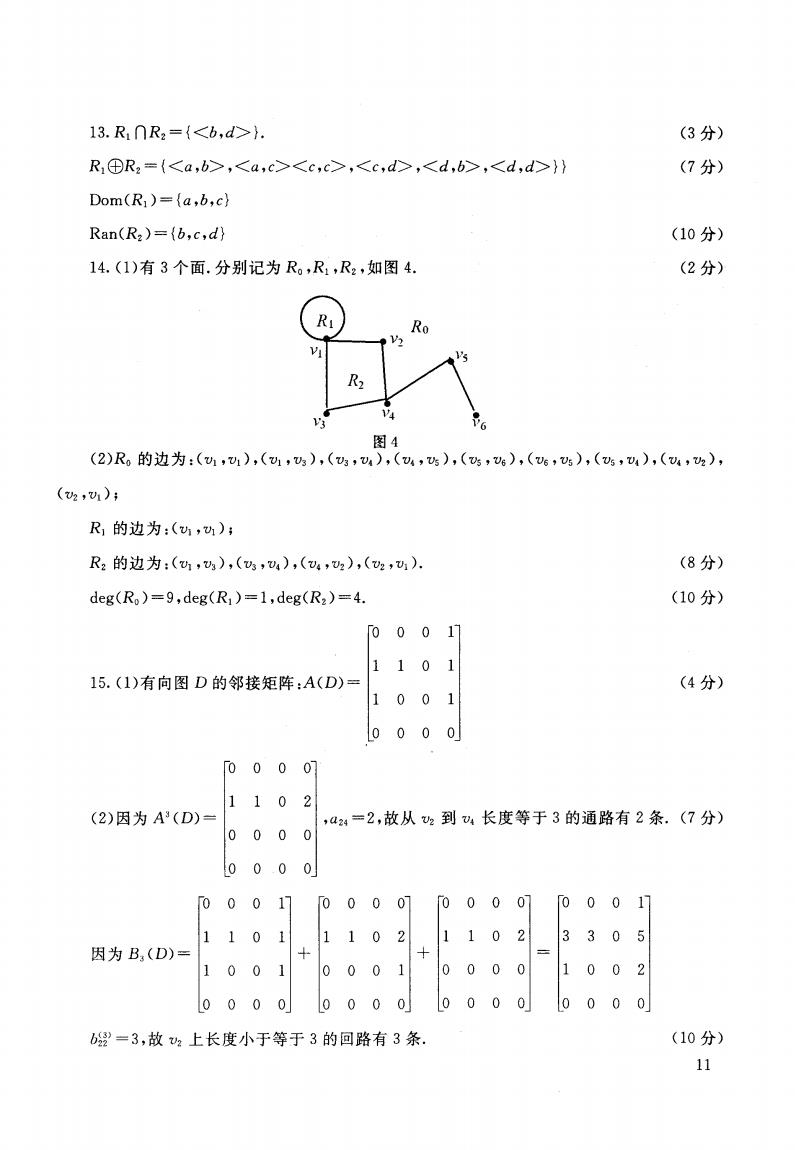
13.R1∩R2={} (3分) R⊕R2={,,,,} (7分) Dom(R)=(a,b,c) Ran(R2)=(b,c,d) (10分) 14.(1)有3个面.分别记为R。,R1,R2,如图4. (2分) R Ro R2 VG 图4 (2)R的边为:(1,),(1,),(3,4),(4,),(,6),(6,),(5,4),(4,h), (,w1); R1的边为:(少,边); R2的边为:(,),(3,⑦4),(4,2),(2,U1) (8分)》 deg(Ro)=9,deg(R1)=1,deg(R2)=4. (10分) [000 17 1101 15.(1)有向图D的邻接矩阵:A(D)= (4分) 1 001 000 000] 1102 (2)因为A3(D) ,a24=2,故从2到⑦4长度等于3的通路有2条.(7分) 0 00 0 000 0 [000 0 000] 00001 [0001] 1101 110 2 1102 3305 因为B,(D)= 1001 0 001 0 000 1002 0000 0 000 00 00 o 000 b=3,故2上长度小于等于3的回路有3条. (10分) 11
13. R,门R2={ }. R,①R2={,, ,, }} Dom (R,)=(a,b,c) Ran(R2)={b, c, d} 14.0)有 3个面.分别记为 Ro ,R R2,如图 4. (3分) (7分) (10分) (2分) (2 )R。的边为:(VI,v,),(v vs),(v3,v4),(v4,v5),(v5,v6)I(vs,vs),(vs,v4),(v4,v2)I (v2 , v4); R,的边为 :(Vi ,v1); R:的边为 :(v v3),(v3,v4),(v4,v2),(v2,v,). (8分) deg(R,)=9,deg(R,)=1,deg(R2)=4. (10分) 15.0)有向图 D 的邻接矩阵 :A(D) = 0 0 1 0 0 0 0 0 (4分) (2)因为 A'(D)= 0 0 1 0 0 0 0 0 ,a24 =2,故从 v2到 v;长度等于 3的通路有 2条.(7分) 因为 B,,(D)= 0 0 3 0 0 0 0 0 姚3z' = 3,故 v:上长度小于等于 3的回路有 3条 (10分) 11

四、证明题(本题共10分) 16.前提:P+(QVR),S→Q,P,S 结论:R 证明 ①P 前提引入(P) ②P→(QVR) 前提引人(P) ③QVP T①,②假言推理 ④S+Q 前提引入(P) (5分) ⑤S 前提引入(P) ⑥Q T⑤,④假言推理 ⑦R T⑥,③析取三段论 分) 12
四、证明题(本题共 10分) 16.前提:P-(QV R),S- , Q,P,S 结论 :R 证明 01 P 前提引人(尸) )P-(QVR) 前提引人(P) ③Qv尸 TOO,O假言推理 (Is~ 二Q 前提引入(P) Os 前提引人(尸) ⑥ ,Q TOO , 假言推理 ⑦ R T) ,③析取三段论 (5分) (10分)