
课程信息 ·教材:《实用多元统计分析》R.A.Johnson and D.W.Wichern 著,清华大学出版社,2008第6版.(英文版和中文版) ·参考教材: An Introduction to Multivariate Statistical Analysis,2003(3rd). T.W.Anderson,Wiely. Applied Multivariate Statistical Analysis,2011(3rd ed), W.K.Hardle,L.Simar,Springer. -Exploratory Multivariate Analysis by Example Using R.2017,Francois Husson,Sebastien Le,Jerome Pages, Chapman and Hall/CRC. 一实用多元统计分析,方开泰,华东师范大学出版社 Previous Next First Last Back Forward 1
课程信息 • 教材:《实用多元统计分析》R.A. Johnson and D.W. Wichern 著, 清华大学出版社, 2008 第 6 版. (英文版和中文版) • 参考教材: – An Introduction to Multivariate Statistical Analysis, 2003(3rd), T.W.Anderson, Wiely. – Applied Multivariate Statistical Analysis, 2011(3rd ed), W. K. Härdle, L. Simar, Springer. – Exploratory Multivariate Analysis by Example Using R, 2017, Francois Husson, Sebastien Le, Jérôme Pagès, Chapman and Hall/CRC. – 实用多元统计分析, 方开泰, 华东师范大学出版社. Previous Next First Last Back Forward 1

一应用多元统计分析,高慧璇,北京大学出版社 ·成绩评定:20/100作业和15/100上机作业,45/100期中考试, 20/100期末project 。课程内容结构: 线性代数 1-4章 统计推断 协方差结构分析 分炎和判别 5-7章 8-10童 11-12章 多元正态分布 主成分分析、 线性分类, 因子分析 聚类分析、 多维标度法等 机器学习,课程主要内容 Previous Next First Last Back Forward 2
– 应用多元统计分析, 高慧璇, 北京大学出版社 • 成绩评定: 20/100 作业和 15/100 上机作业, 45/100 期中考试, 20/100 期末 project • 课程内容结构: Previous Next First Last Back Forward 2

1.1 简介 ·多元数据:许多观测或者设计研究中,每个试验单元()的多 个指标(p)被同时观测收集 Xi=(Xi,...,Xip),i=1,...:n 。多元分析是一类运用线性代数知识,分析处理多元数据的统计 方法或机器学习/人工智能方法, ·相比于一元分析,多元分析利用多个变量之间的潜在相关性来 提升推断效率 ,一些多元数据分析技术基于特定的概率模型,特别是多元正态分布, 其他不依赖于特定分布的方法称为“模型自由的”(model-ree) Previous Next First Last Back Forward 3
1.1 简介 • 多元数据: 许多观测或者设计研究中, 每个试验单元 (n) 的多 个指标 (p) 被同时观测收集 Xi = (Xi1, . . . , Xip), i = 1, . . . , n • 多元分析是一类运用线性代数知识,分析处理多元数据的统计 方法或机器学习/人工智能方法. • 相比于一元分析,多元分析利用多个变量之间的潜在相关性来 提升推断效率 • 一些多元数据分析技术基于特定的概率模型, 特别是多元正态分布, 其他不依赖于特定分布的方法称为 “模型自由的” (model-free) Previous Next First Last Back Forward 3

数据的组织 ·n个观测,p个变量(表示为数据矩阵) 变量1 变量2 变量p Item 1 Obs 1 E11 E12 4 Tip Item 2 Obs 2 T21 T22 4 工2P .. Item n Obs n Inl 工n2 Enp x秋:第i个个体的第k个变量值. 常用矩阵表示 E11 E12 士1p 工21 E22 烟 X= 工2P or X= In1 In2 np x Previous Next First Last Back Forward 4
数据的组织 • n 个观测, p 个变量:(表示为数据矩阵) 变量 1 变量 2 · · · 变量 p Item 1 Obs 1 x11 x12 · · · x1p Item 2 Obs 2 x21 x22 · · · x2p . . . . . . . . . . . . . . . Item n Obs n xn1 xn2 · · · xnp xik : 第 i 个个体的第 k 个变量值. 常用矩阵表示 X = x11 x12 · · · x1p x21 x22 · · · x2p . . . . . . . . . . . . xn1 xn2 · · · xnp or X = x T 1 x T 2 . . . x T n Previous Next First Last Back Forward 4

数据的特点 ·测量的类型 -名义尺度(Nominal):类别变量,顺序没有意义.例如性 别,颜色 -有序尺度(Ordinal):类别变量,顺序有意义.例如等级 -区间尺度(Interval):数值的差有意义,没有固定的0位 置.例如温度,海拔,纪年 -比例尺度(Ratio):数值变量,比值是有意义的,具有固定 的0值位置.例如高度,年龄,体重等。 根据数据的测量类型选择合适的统计方法 Previous Next First Last Back Forward 5
数据的特点 • 测量的类型 – 名义尺度 (Nominal): 类别变量, 顺序没有意义. 例如性 别, 颜色 – 有序尺度 (Ordinal): 类别变量, 顺序有意义. 例如等级 – 区间尺度 (Interval): 数值的差有意义, 没有固定的 0 位 置. 例如温度, 海拔, 纪年 – 比例尺度 (Ratio): 数值变量, 比值是有意义的, 具有固定 的 0 值位置. 例如高度, 年龄, 体重等. 根据数据的测量类型选择合适的统计方法 Previous Next First Last Back Forward 5

·数据缺失问题: 一测量很多变量时,常遇到其中一些变量观测值缺失的情况 一一种做法:完全数据分析一删除观测变量中具有缺失值的 个体,使用没有缺失值的个体观测进行推断 一问题:可能会导致许多观测被删除,从而大大减少了样本 量 -问题:可以导致有偏估计,除非缺失数据为MCAR(missing completely at random)的(缺失是完全随机的,与观测到 的变量和感兴趣的参数等独立) 更佳的解决方法:使用多重插值(multiple imputation), 对缺失值进行补缺 ·维数灾难问题:p大于n.大部分经典方法不能使用. Previous Next First Last Back Forward 6
• 数据缺失问题: – 测量很多变量时, 常遇到其中一些变量观测值缺失的情况 – 一种做法: 完全数据分析—删除观测变量中具有缺失值的 个体, 使用没有缺失值的个体观测进行推断 – 问题: 可能会导致许多观测被删除, 从而大大减少了样本 量 – 问题: 可以导致有偏估计, 除非缺失数据为 MCAR(missing completely at random) 的 (缺失是完全随机的, 与观测到 的变量和感兴趣的参数等独立) – 更佳的解决方法: 使用多重插值 (multiple imputation), 对缺失值进行补缺. • 维数灾难问题:p 大于 n. 大部分经典方法不能使用. Previous Next First Last Back Forward 6

1.2 多元方法的应用 例1:瓷器化学成分 三个不同地区出土的若千瓷器测量9种不同的化学成分(A12O3,F2O3 等),部分瓷器(10件)数据如下 IDA1203 Fe203 Mgo Ca0 Na20 K20 Ti02 Mn0 Ba0 Region 118.89.5220.790.43.21.010.0770.015 1 216.97.331.650.840.43.050.990.0670.018 1 318.27.641.820.770.43.070.980.0870.014 1 416.97.291.560.760.43.0510.0630.019 1 514.474.30.150.514.250.790.160.019 2 613.87.065.340.20.24.310.710.1010.021 2 714.67.093.880.130.24.360.810.1240.019 2 815.82.390.630.010.041.941.290.0010.014 3 9181.50.670.010.062.110.920.0010.016 3 10 181.880.680.010.0421.110.0060.022 3 感兴趣的问题包括: Previous Next First Last Back Forward
1.2 多元方法的应用 例 1:瓷器化学成分 三个不同地区出土的若干瓷器测量 9 种不同的化学成分 (Al2O3,Fe2O3 等), 部分瓷器(10 件)数据如下 感兴趣的问题包括: Previous Next First Last Back Forward 7

(1)三个地区的化学成分测量值是否不同?统计检验 (2)能否用少数几个指标代替原来的9个指标(降维)?如何画图展 示数据?降维、可视化 (3)如何根据化学成分测量值判别瓷器的产地?判别分类、预测 (4)假如没有最后一列Region,能否发现这些样本来自于三个地 方?是否有某几个指标测量的是同一种属性?聚类分析 Previous Next First Last Back Forward F
(1) 三个地区的化学成分测量值是否不同?统计检验 (2) 能否用少数几个指标代替原来的 9 个指标 (降维)?如何画图展 示数据?降维、可视化 (3) 如何根据化学成分测量值判别瓷器的产地?判别分类、预测 (4) 假如没有最后一列 Region,能否发现这些样本来自于三个地 方?是否有某几个指标测量的是同一种属性?聚类分析 Previous Next First Last Back Forward 8

例2:基因组数据 2504个人的基因组数据,每个人在9932个位点上的基因值为0, 1,2.每个人的种族为:AFR(African),AMR(American),EAS(East Asian),EUR(European),SAS(South Asian)。部分数据如下: Race V1V2V3V4V5V6V78V9V10V11V12V13V14V15V16V17V18V19V20 AFR 20012021120012122 200 AMR 20002 0 200000020211 0 AFR 2101202101001 212220 0 SAS 2000201011 000 20 20 2 0 EAS 2 0 01212012000 20 0 1 2 0 0 EAS 0 00201000000 2 1 2 0 EUR 2 0020211100 0 0 0 0 EUR 2 0 0122200100 0 2 2 2 0 AMR 20 00 20210100 0 2 0 2 0 0 SAS 2 0 0120200100121222 0 数据为2504x9933矩阵(第一列为Race) 各种族的基因是否有差异?如何直观视图展示各种族的差异? Previous Next First Last Back Forward
例 2: 基因组数据 2504 个人的基因组数据,每个人在 9932 个位点上的基因值为 0, 1, 2. 每个人的种族为:AFR (African), AMR(American), EAS (East Asian), EUR (European), SAS (South Asian)。部分数据如下: 数据为 2504 x 9933 矩阵(第一列为 Race) 各种族的基因是否有差异?如何直观视图展示各种族的差异? Previous Next First Last Back Forward 9
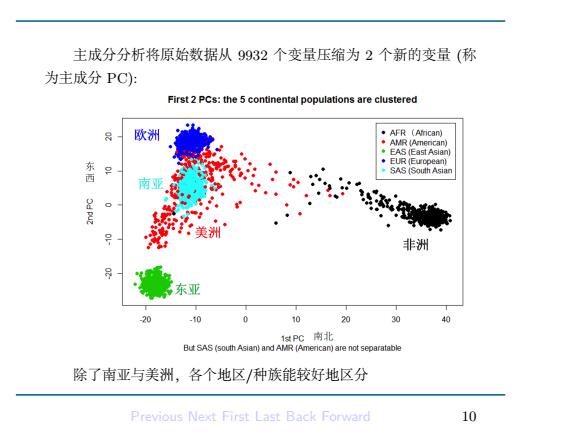
主成分分析将原始数据从9932个变量压缩为2个新的变量(称 为主成分PC): First 2 PCs:the 5 continental populations are clustered 8 欧洲 .AFR (Afican) ◆AMR(merican) EAS (East Asian) ◆EUR (Eucpean) 东 SAS (South Asian 洲 非洲 东亚 20 10 10 20 30 1仗PC南北 But SAS (south Asian)and AMR (American)are not separatable 除了南亚与美洲,各个地区/种族能较好地区分 Previous Next First Last Back Forward 10
主成分分析将原始数据从 9932 个变量压缩为 2 个新的变量 (称 为主成分 PC): 除了南亚与美洲,各个地区/种族能较好地区分 Previous Next First Last Back Forward 10