
简介 1.1 简介 1 1.2 总体主成分 3 1.3 样本主成分 16 1.4 大样本性质.· 22 1.5PCA和SVD 26 1.6PCA的应用 28 Previous Next First Last Back Forward 1
简介 1.1 简介 . . . . . . . . . . . . . . . . . . . . . . . 1 1.2 总体主成分 . . . . . . . . . . . . . . . . . . . 3 1.3 样本主成分 . . . . . . . . . . . . . . . . . . . 16 1.4 大样本性质 . . . . . . . . . . . . . . . . . . . 22 1.5 PCA 和 SVD . . . . . . . . . . . . . . . . . . 26 1.6 PCA 的应用 . . . . . . . . . . . . . . . . . . . 28 Previous Next First Last Back Forward 1

1.1 简介 ·高维数据存在的问题:维数灾难(curse of dimensionality,p》 n) 一运算时间 一过拟合 -需要的样本量大小(达到同样的精度,需要样本量) ·维数减低技术:希望用较少的变量来代替原来较多的变量,而 这些较少的变量尽可能反映原来变量的信息 ·维数降低技术包括主成分分析,因子分析,典型相关分析,多维 标度法,神经网络,流行学习等等 Previous Next First Last Back Forward 1
1.1 简介 • 高维数据存在的问题: 维数灾难 (curse of dimensionality, p ≫ n) – 运算时间 – 过拟合 – 需要的样本量大小 (达到同样的精度, 需要样本量 n d ) • 维数减低技术: 希望用较少的变量来代替原来较多的变量, 而 这些较少的变量尽可能反映原来变量的信息. • 维数降低技术包括主成分分析, 因子分析, 典型相关分析, 多维 标度法, 神经网络, 流行学习等等. Previous Next First Last Back Forward 1

主成分分析(PCA,Principal components analysis) ·一种自然的想法就是将数据线性投影到低维空间:记个观测 的m维数据矩阵为Xmxn,寻找变换矩阵Paxm,d《m,则 Y=PX,即将原始m维数据点在d维空间表示.选择合适的 目标(准则)函数后,寻找最优的投影阵A. ·主成分分析方法就是寻找d个原来变量的线性组合,使得它们 保留了大部分方差波动性, ·这些由原来变量的线性组合构成的变量即称为主成分 ·主成分分析可以用来检测样本点中的异常点,在低维空间表达 原始数据以发现可能存在的模式 ·(样本)主成分的得分常常作为响应变量,以进行下一步分析(回 归,聚类,判别等等)的基础. Previous Next First Last Back Forward 2
主成分分析 (PCA, Principal components analysis) • 一种自然的想法就是将数据线性投影到低维空间: 记 n 个观测 的 m 维数据矩阵为 Xm×n, 寻找变换矩阵 Pd×m, d ≪ m, 则 Y = PX, 即将原始 m 维数据点在 d 维空间表示. 选择合适的 目标 (准则) 函数后, 寻找最优的投影阵 A. • 主成分分析方法就是寻找 d 个原来变量的线性组合, 使得它们 保留了大部分方差波动性. • 这些由原来变量的线性组合构成的变量即称为主成分 • 主成分分析可以用来检测样本点中的异常点, 在低维空间表达 原始数据以发现可能存在的模式 • (样本) 主成分的得分常常作为响应变量, 以进行下一步分析 (回 归, 聚类, 判别等等) 的基础. Previous Next First Last Back Forward 2

1.2 总体主成分 ·假设随机向量X=(X1,.,X)'的协方差矩阵∑有特征根 入1≥2≥…2入p≥0 ·考虑p个线性组合 Yi=aiX a11X1+...+aipXp Y2 a2X a21X1+...+a2pXp Yp apx apIX1+...+appXp ·Y,…,Y。称为主成分.我们有 Var(Yi)=aiEai,i=1,...,p Cov(Yi,Yj)=aiSaj,aj,i,j=1,...,p Previous Next First Last Back Forward 3
1.2 总体主成分 • 假设随机向量 X = (X1, . . . , Xp) ′ 的协方差矩阵 Σ 有特征根 λ1 ≥ λ2 ≥ · · · ≥ λp ≥ 0 • 考虑 p 个线性组合 Y1 = a ′ 1X = a11X1 + · · · + a1pXp Y2 = a ′ 2X = a21X1 + · · · + a2pXp . . . Yp = a ′ pX = ap1X1 + · · · + appXp • Y1, . . . , Yp 称为主成分. 我们有 V ar(Yi) = a ′ iΣai, i = 1, . . . , p Cov(Yi, Yj ) = a ′ iΣaj , aj , i, j = 1, . . . , p Previous Next First Last Back Forward 3

·选择单位向量a,使得Var(Y)≥Var()≥…≥Var(Yp) 且,,yp不相关.可以通过如下过程得到这样的向量a: 1.d1 arg max aia ‖a1I=1 2.a2=arg max 吃a2 ‖a2ll=1,a42a1=0 3.di=arg max ,a∑a llai=1,aEak=0,k<i .. 4.dp arg. max pEap apl=1,aEak=0,k<p Previous Next First Last Back Forward 4
• 选择单位向量 ai, 使得 V ar(Y1) ≥ V ar(Y2) ≥ · · · ≥ V ar(Yp) 且 Y1, . . . , Yp 不相关. 可以通过如下过程得到这样的向量 ai: 1. aˆ1 = arg max ∥a1∥=1 a ′ 1Σa1 2. aˆ2 = arg max ∥a2∥=1,a′ 2Σˆa1=0 a ′ 2Σa2 . . . 3. aˆi = arg max ∥ai∥=1,a′ iΣˆak=0,k<i a ′ iΣai . . . 4. aˆp = arg max ∥ap∥=1,a′ pΣˆak=0,k<p a ′ pΣap Previous Next First Last Back Forward 4

定理1.设随机向量X=(X1,·,X)了的协方差矩阵∑有特征根 和特征向量(以,p),i=1,,p,且入1≥2≥…≥入p≥0.则满 足上述过程的单位向量à为 ai=,i=1,..,p. 证明.由代数事实(课本2.7节)有 maxa'∑a=X1,最大值在a1=1处达到 lal=1 max a∑a=Xk,最大值在ak=中k处达到 al=1,a1p1,k-1 注意到a∑ak=a∑中k=ka4pk=0,k<i台ai⊥1,,pi-1, 从而由上述代数事实立证. 口 Previous Next First Last Back Forward 5
定理 1. 设随机向量 X = (X1, . . . , Xp) ′ 的协方差矩阵 Σ 有特征根 和特征向量 (λi, ϕi), i = 1, . . . , p, 且 λ1 ≥ λ2 ≥ · · · ≥ λp ≥ 0. 则满 足上述过程的单位向量 aˆ 为 aˆi = ϕi, i = 1, . . . , p. 证明. 由代数事实 (课本 2.7 节) 有 max ∥a∥=1 a ′Σa = λ1, 最大值在aˆ1 = ϕ1处达到 max ∥a∥=1,a⊥ϕ1,...,ϕk−1 a ′Σa = λk, 最大值在aˆk = ϕk处达到 注意到 a ′ iΣˆak = a ′ iΣϕk = λka ′ iϕk = 0, k < i ⇔ ai ⊥ ϕ1, . . . , ϕi−1, 从而由上述代数事实立证. Previous Next First Last Back Forward 5

·此时 Var(Ya)=p∑φ=λipip:=λ: Cou(Y,Yk)=∑bk=入kppk=0,i≠k ·因此主成分方法将相关的变量X1,,Xp转换为不相关的变 量Y,,yp,且 Var=aa四=+…+-ar0价 Previous Next First Last Back Forward 6
• 此时 V ar(Yi) = ϕ ′ iΣϕ = λiϕ ′ iϕi = λi Cov(Yi, Yk) = ϕ ′ iΣϕk = λkϕ ′ iϕk = 0, i ̸= k • 因此主成分方法将相关的变量 X1, . . . , Xp 转换为不相关的变 量 Y1, . . . , Yp. 且 ∑p i=1 V ar(Xi) = trace(Σ) = λ1 + · · · + λp = ∑p i=1 V ar(Yi) Previous Next First Last Back Forward 6
·第k个主成分Y:所占的方差比例 入k ,k=1,,p 入1+·+入p ·如果前d个(化=1,,d.)主成分所能解释的总的方差比例超 过80%(经验上),则可以使用这前d个主成分来表示原来变量, 这样做仅仅损失少量信息. Previous Next First Last Back Forward 1
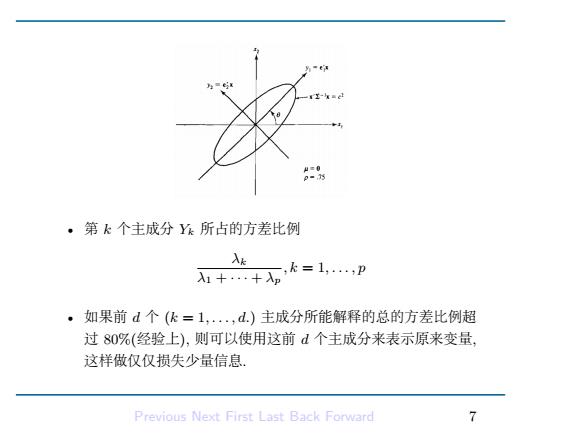
• 第 k 个主成分 Yk 所占的方差比例 λk λ1 + · · · + λp , k = 1, . . . , p • 如果前 d 个 (k = 1, . . . , d.) 主成分所能解释的总的方差比例超 过 80%(经验上), 则可以使用这前 d 个主成分来表示原来变量, 这样做仅仅损失少量信息. Previous Next First Last Back Forward 7

·第:个主成分和第k个原始变量之间的相关系数为 Cou(oX,ekx) PyXk= VVar(Yi)Var(Xk) V八:0kk √Okk 度量了第k个变量对第i个主成分的贡献.其中k=[0,.,0,1,0,,0 使得Xk=ekX. ·py,x仅仅衡量Xk对上的贡献,而不管其他变量.因此一些 学者建议仅使用中k来衡量变量Xk对主成分Y的重要程度, 根据中:的(绝对值)值对原始p个变量从大到小排序,来表示 原始变量对主成分Y的重要性排序 ·前m个主成分Y,Y,…,Ym与原变量Xk(1≤k≤p)的 各相关系数的平方和称为Y,Y2,…·,Ym对Xk的方差贡献率 (或简称贡献率),记作m(或在不混淆的情况下直接记为,) Previous Next First Last Back Forward
• 第 i 个主成分和第 k 个原始变量之间的相关系数为 ρYi,Xk = Cov(ϕ ′ iX, e′ kX) √ V ar(Yi)V ar(Xk) = ϕ ′ iΣek √ λiσkk = ϕik√ λi √ σkk 度量了第 k 个变量对第 i 个主成分的贡献. 其中 e ′ k = [0, . . . , 0, 1, 0, . . . , 0], 使得 Xk = e ′ kX. • ρYi,Xk 仅仅衡量 Xk 对 Yi 的贡献, 而不管其他变量. 因此一些 学者建议仅使用 ϕik 来衡量变量 Xk 对主成分 Yi 的重要程度, 根据 ϕi 的 (绝对值) 值对原始 p 个变量从大到小排序, 来表示 原始变量对主成分 Yi 的重要性排序. • 前 m 个主成分 Y1, Y2, · · · , Ym 与原变量 Xk (1 ≤ k ≤ p) 的 各相关系数的平方和称为 Y1, Y2, · · · , Ym 对 Xk 的方差贡献率 (或简称贡献率), 记作 ν (m) k (或在不混淆的情况下直接记为 νk), Previous Next First Last Back Forward 8

即有 1 Vk= Xa,k=1,2,…,p. 设三维随机向量X=(X1,X2,X3)'的协方差阵为 TExample 求其相应的主成分. ⊥Example 首先,经过简单计算可得∑的特征值以及对应的单位特征向量分 Previous Next First Last Back Forward 9
即有 νk = 1 σkk ∑m i=1 λia 2 ki, k = 1, 2, · · · , p. ↑Example 设三维随机向量 X = (X1, X2, X3) ′ 的协方差阵为 Σ = 1 −2 0 −2 5 0 0 0 2 . 求其相应的主成分. ↓Example 首先, 经过简单计算可得 Σ 的特征值以及对应的单位特征向量分 Previous Next First Last Back Forward 9