
Clustering Lecture 6:Spectral Methods Jing Gao SUNY Buffalo 1
Clustering Lecture 6: Spectral Methods Jing Gao SUNY Buffalo 1

Outline ·Basics Motivation,definition,evaluation ·Methods -Partitional Hierarchical Density-based -Mixture model -Spectral methods Advanced topics Clustering ensemble Clustering in MapReduce -Semi-supervised clustering,subspace clustering,co-clustering, etc
Outline • Basics – Motivation, definition, evaluation • Methods – Partitional – Hierarchical – Density-based – Mixture model – Spectral methods • Advanced topics – Clustering ensemble – Clustering in MapReduce – Semi-supervised clustering, subspace clustering, co-clustering, etc. 2
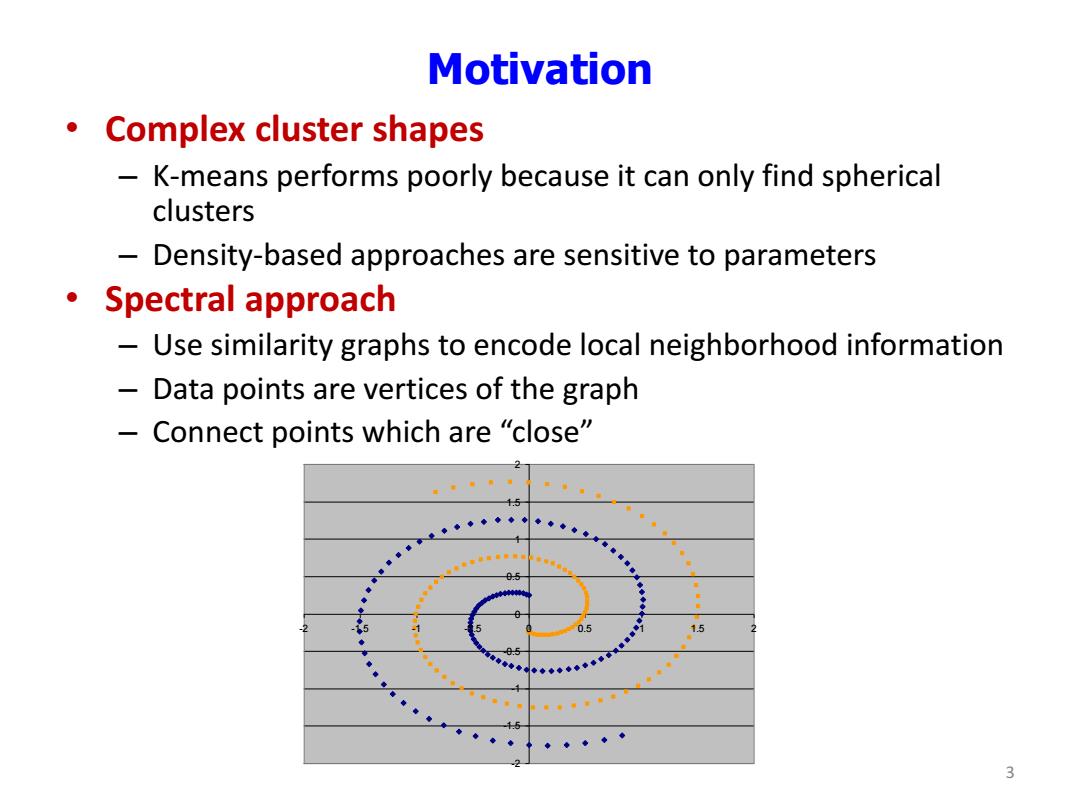
Motivation Complex cluster shapes - K-means performs poorly because it can only find spherical clusters Density-based approaches are sensitive to parameters 。Spectral approach Use similarity graphs to encode local neighborhood information Data points are vertices of the graph Connect points which are "close" 1.5 15 3
Motivation • Complex cluster shapes – K-means performs poorly because it can only find spherical clusters – Density-based approaches are sensitive to parameters • Spectral approach – Use similarity graphs to encode local neighborhood information – Data points are vertices of the graph – Connect points which are “close” 3 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2

Similarity Graph Represent dataset as a weighted graph G,E) All vertices which can be reached from each other by a path form a connected component Only one connected component in the graph-The graph is fully connected V=x;}Set of n vertices representing data points E={W}Set of weighted edges indicating pair-wise similarity between points 0.1 0.8 0.8 0.8 0.6 6 0.7 0.8 3 0.2 4
0.1 0.2 0.8 0.7 0.6 0.8 0.8 0.8 E={Wij} Set of weighted edges indicating pair-wise similarity between points Similarity Graph • Represent dataset as a weighted graph G(V,E) • All vertices which can be reached from each other by a path form a connected component • Only one connected component in the graph—The graph is fully connected 1 2 6 { , ,..., } v v v 1 2 3 4 5 6 V={xi } Set of n vertices representing data points 4

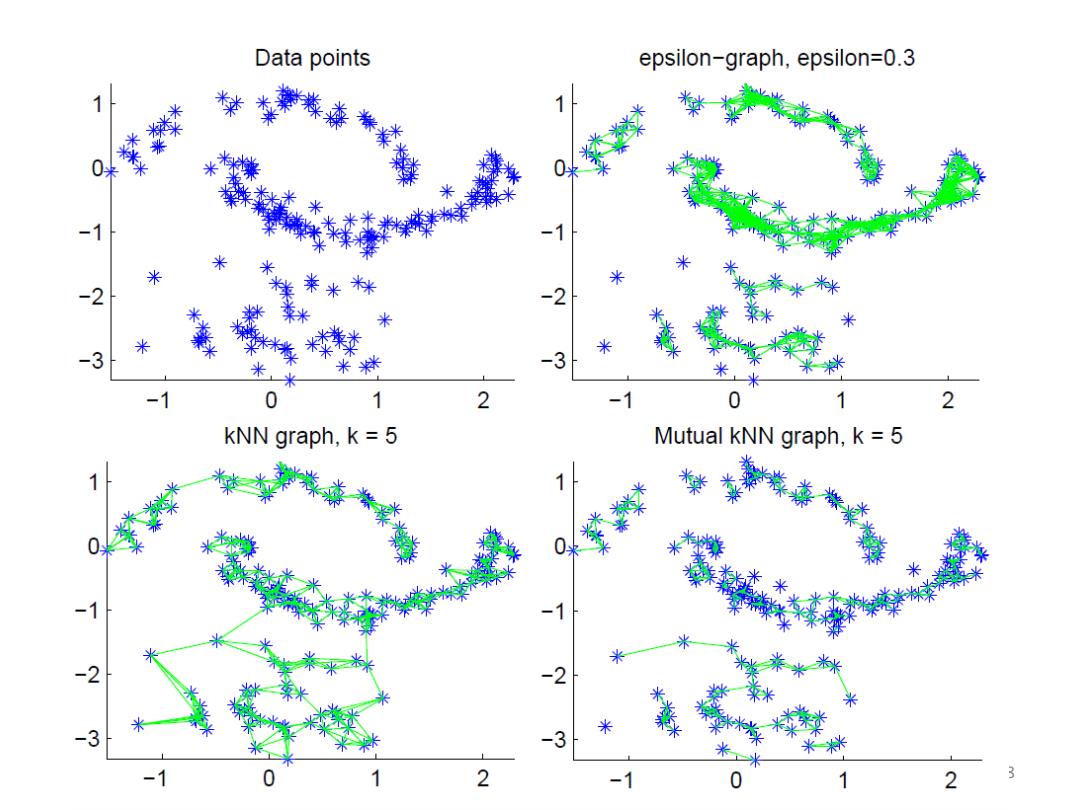
Graph Construction E-neighborhood graph Identify a threshold value,s,and include edges if the affinity between two points is greater than k-nearest neighbors Insert edges between a node and its k-nearest neighbors Each node will be connected to (at least)k nodes ·Fully connected Insert an edge between every pair of nodes Weight of the edge represents similarity -Gaussian kernel: w,=eXp(-‖x,-x,2/o2) 5
Graph Construction • ε-neighborhood graph – Identify a threshold value, ε, and include edges if the affinity between two points is greater than ε • k-nearest neighbors – Insert edges between a node and its k-nearest neighbors – Each node will be connected to (at least) k nodes • Fully connected – Insert an edge between every pair of nodes – Weight of the edge represents similarity – Gaussian kernel: exp( || || / ) 2 2 wij xi xj 5

sneighborhood Graph 。e-neighborhood Compute pairwise distance between any two objects Connect each point to all other points which have distance smaller than a threshold s Weighted or unweighted Unweighted-There is an edge if one point belongs to the &-neighborhood of another point Weighted-Transform distance to similarity and use similarity as edge weights 6
ε-neighborhood Graph • ε-neighborhood – Compute pairwise distance between any two objects – Connect each point to all other points which have distance smaller than a threshold ε • Weighted or unweighted – Unweighted—There is an edge if one point belongs to the ε–neighborhood of another point – Weighted—Transform distance to similarity and use similarity as edge weights 6

KNN Graph ·Directed graph Connect each point to its k nearest neighbors ·kNN graph Undirected graph An edge between x;and x;:There's an edge from x;to X;OR from x;to x;in the directed graph 。Mutual kNN graph Undirected graph Edge set is a subset of that in the kNN graph An edge between x;and x;:There's an edge from x;to X;AND from x;to x;in the directed graph 7
kNN Graph • Directed graph – Connect each point to its k nearest neighbors • kNN graph – Undirected graph – An edge between xi and xj : There’s an edge from xi to xj OR from xj to xi in the directed graph • Mutual kNN graph – Undirected graph – Edge set is a subset of that in the kNN graph – An edge between xi and xj : There’s an edge from xi to xj AND from xj to xi in the directed graph 7
Data points epsilon-graph,epsilon=0.3 -1 -1 米 米 米 米 米 -2 -2 米 米 -3 米 米 米 -3 0 1 2 0 1 2 kNN graph,k =5 Mutual kNN graph,k =5 米 2 -3 -3 2 1 2 3
8
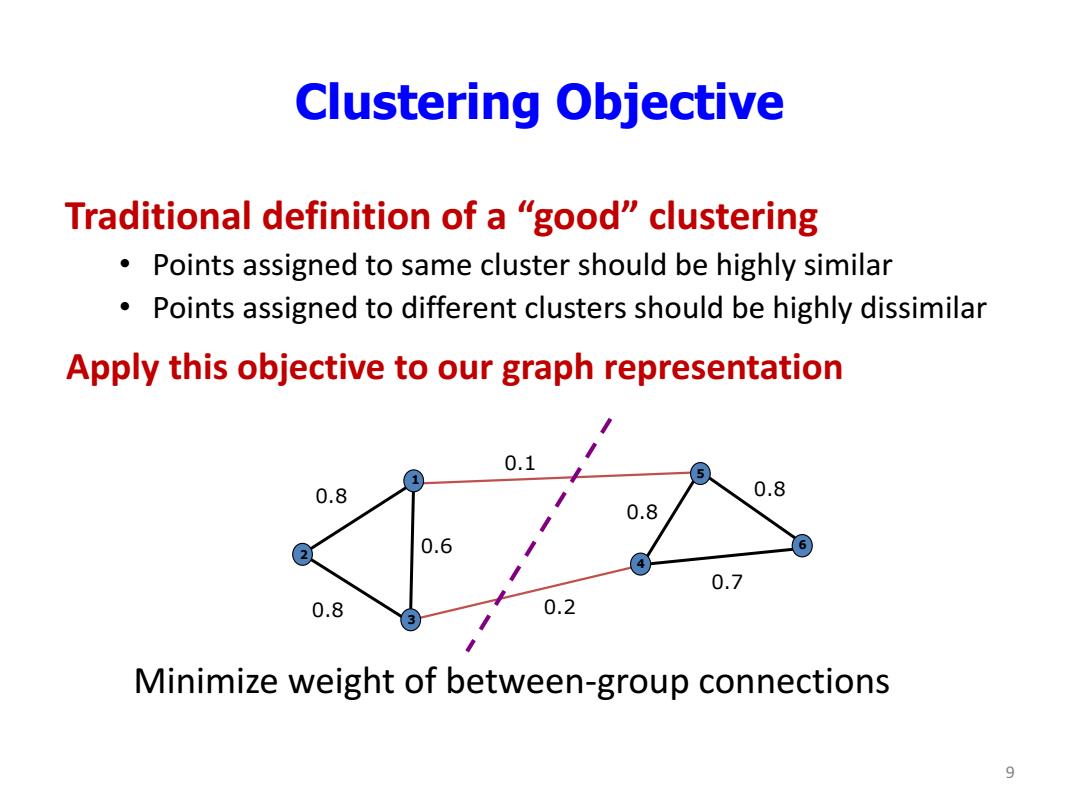
Clustering Objective Traditional definition of a "good"clustering Points assigned to same cluster should be highly similar Points assigned to different clusters should be highly dissimilar Apply this objective to our graph representation 0.1 0.8 0.8 0.8 0.6 6 0.7 0.8 0.2 Minimize weight of between-group connections 9
Clustering Objective Traditional definition of a “good” clustering • Points assigned to same cluster should be highly similar • Points assigned to different clusters should be highly dissimilar Minimize weight of between-group connections 0.1 0.2 0.8 0.7 0.6 0.8 0.8 0.8 1 2 3 4 5 6 Apply this objective to our graph representation 9
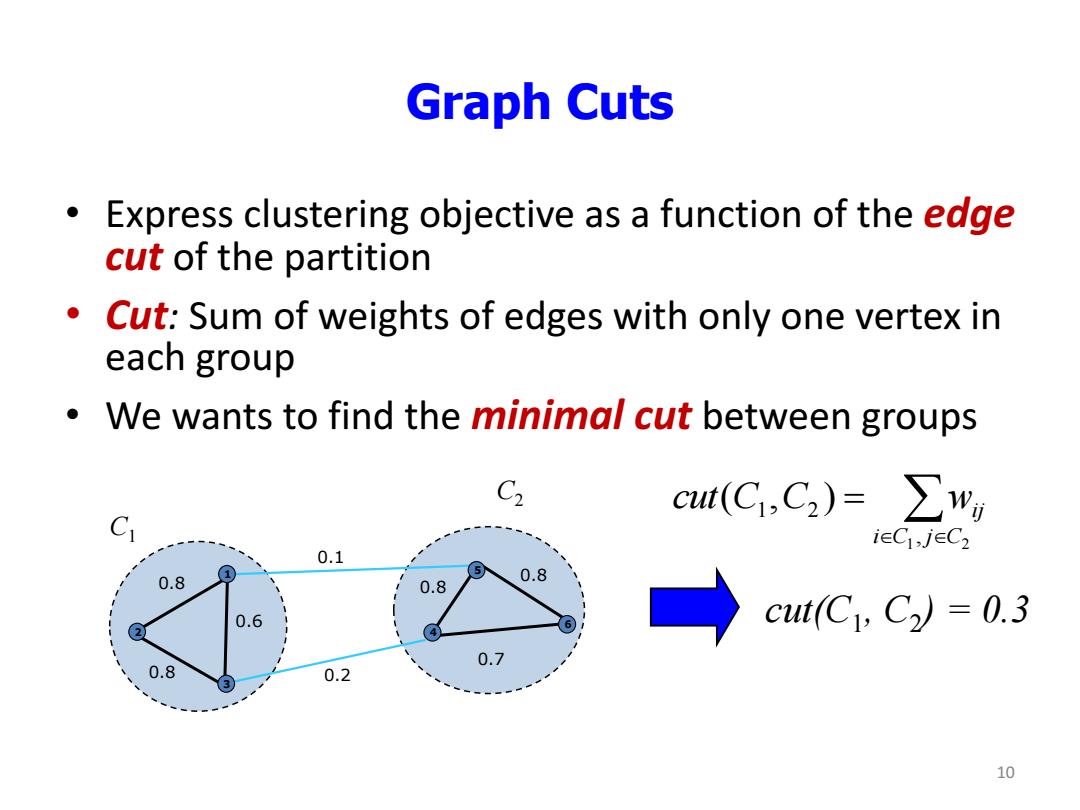
Graph Cuts Express clustering objective as a function of the edge cut of the partition Cut:Sum of weights of edges with only one vertex in each group We wants to find the minimal cut between groups C2 cut(C1,C2)=∑w C ieCl,jEC2 0.1 0.8 0.8 0.8 0.6 6 cut(C1,C2)=0.3 2 0.7 0.8 0.2 10
Graph Cuts • Express clustering objective as a function of the edge cut of the partition • Cut: Sum of weights of edges with only one vertex in each group • We wants to find the minimal cut between groups 1 2 , 1 2 ( , ) i C j C C C wij cut 0.1 0.2 0.8 0.7 0.6 0.8 0.8 1 2 3 4 5 6 0.8 cut(C1 , C2 ) = 0.3 10 C1 C2