
Monte Carlo Integration COS 323 Acknowledgment:Tom Funkhouser
Monte Carlo Integration COS 323 Acknowledgment: Tom Funkhouser
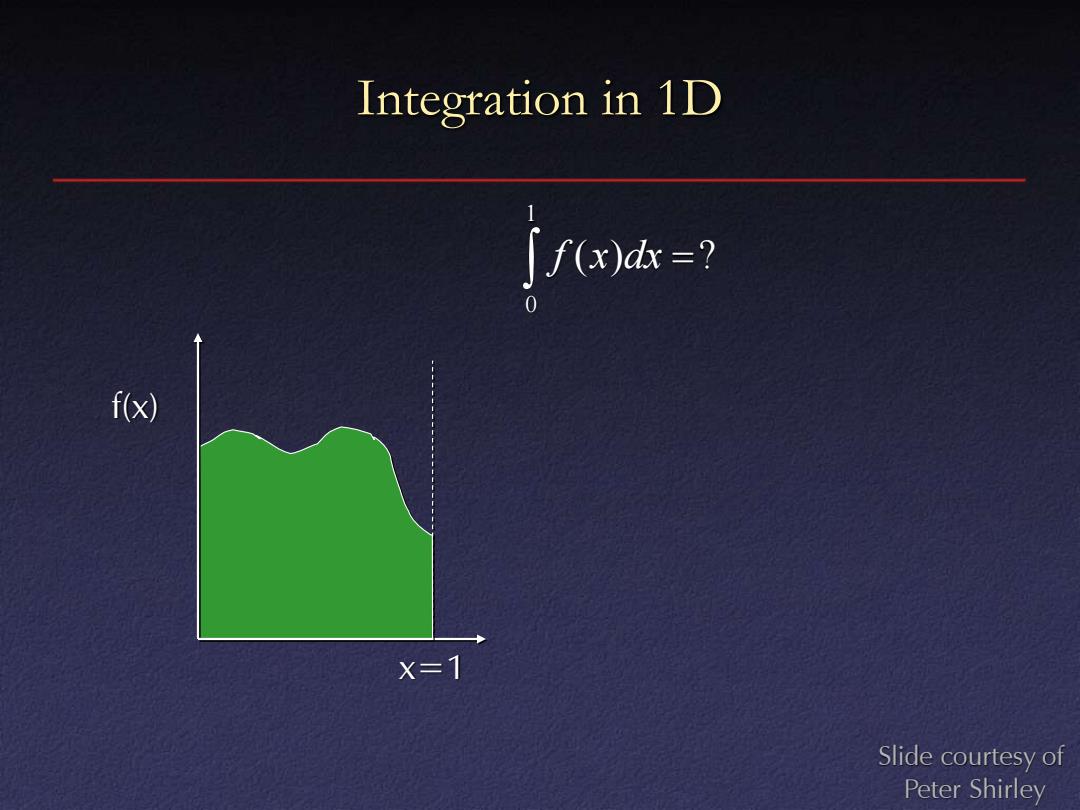
Integration in 1D ∫f(x)k=? f(x) X=1 Slide courtesy of Peter Shirley
Integration in 1D x=1 f(x) ( ) ? 1 0 f x dx = Slide courtesy of Peter Shirley
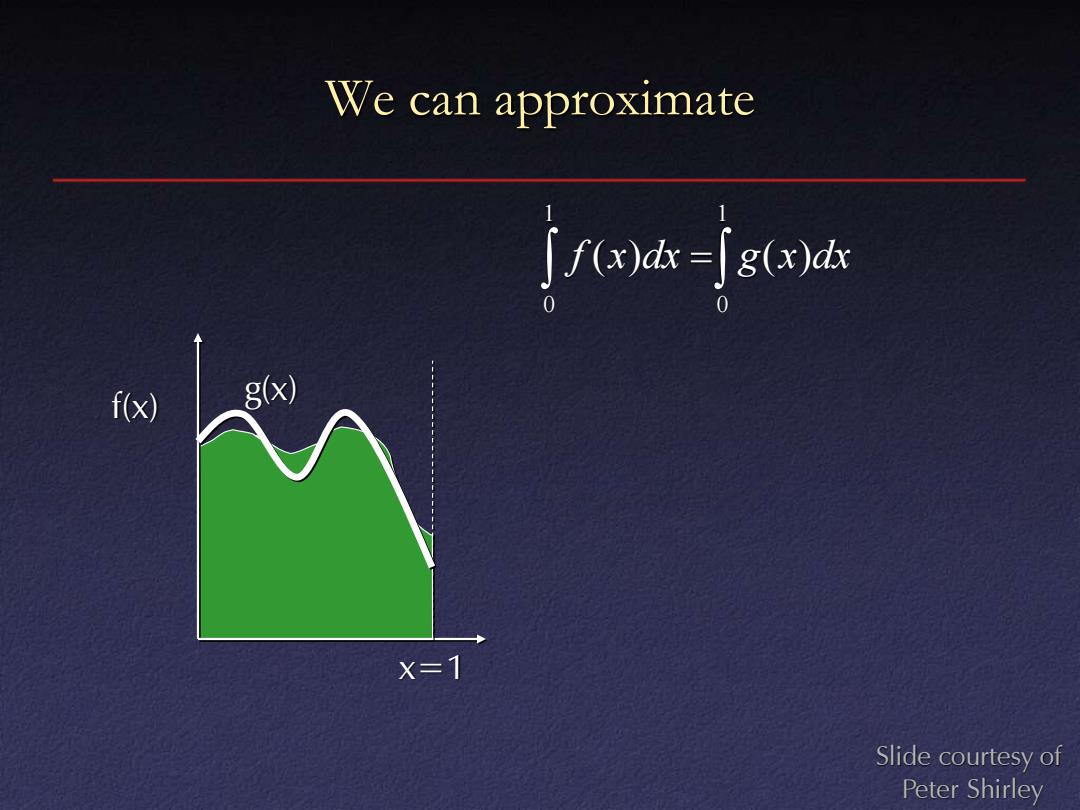
We can approximate ja寸g6a f(x) 8x) X=1 Slide courtesy of Peter Shirley
We can approximate x=1 f(x) g(x) = 1 0 1 0 f (x)dx g(x)dx Slide courtesy of Peter Shirley
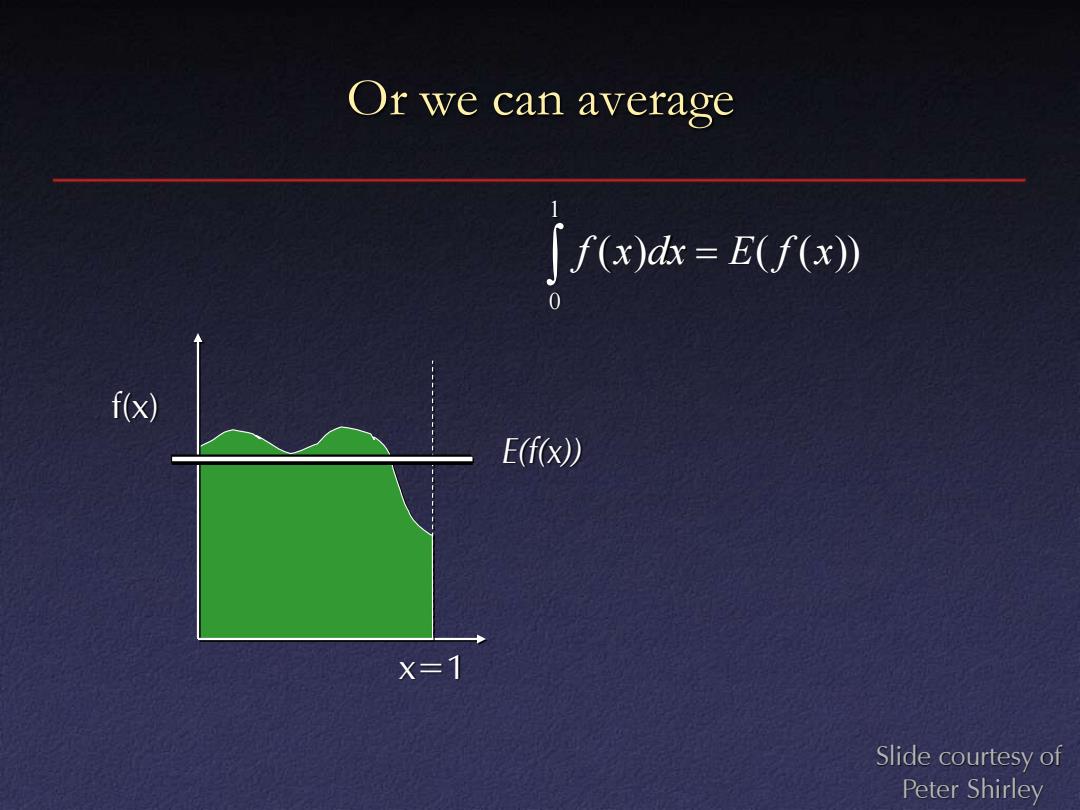
Or we can average 「fx)k=E(fx》 0 f(x) E(f(x)) X=1 Slide courtesy of Peter Shirley
Or we can average x=1 f(x) E(f(x)) ( ) ( ( )) 1 0 f x dx = E f x Slide courtesy of Peter Shirley
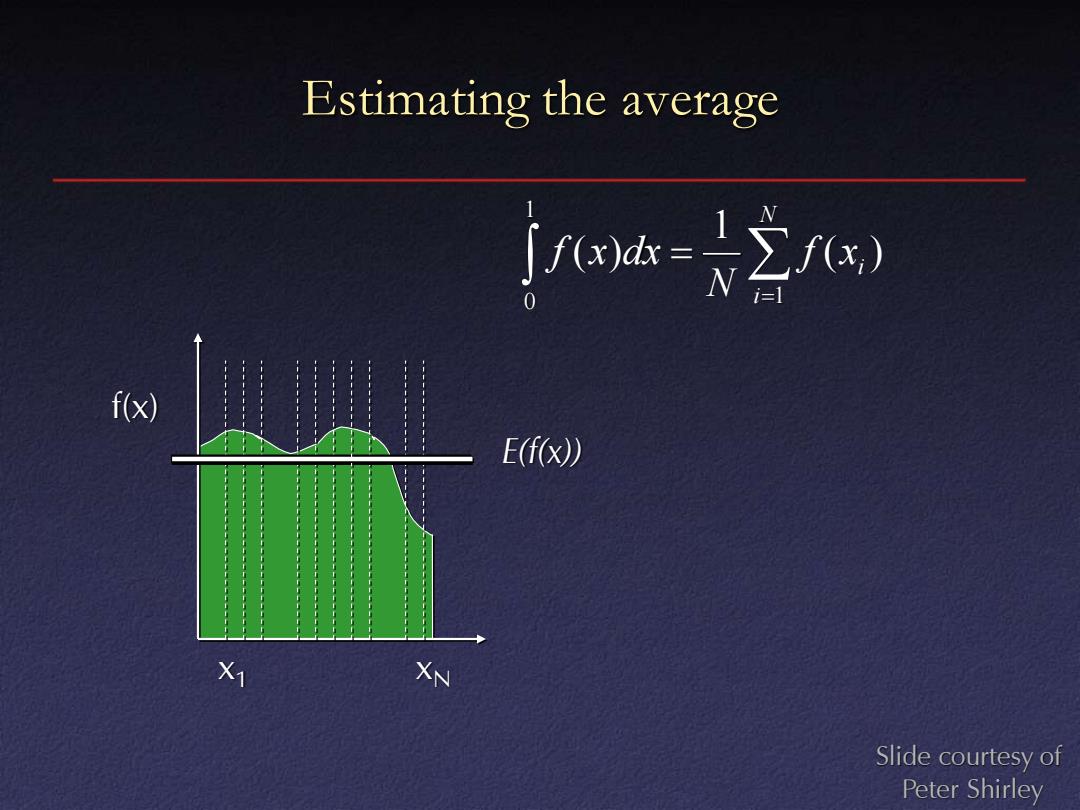
Estimating the average j3=之W f(x) E(f(x)) X1 XN Slide courtesy of Peter Shirley
Estimating the average x1 f(x) xN = = N i i f x N f x dx 1 1 0 ( ) 1 ( ) E(f(x)) Slide courtesy of Peter Shirley
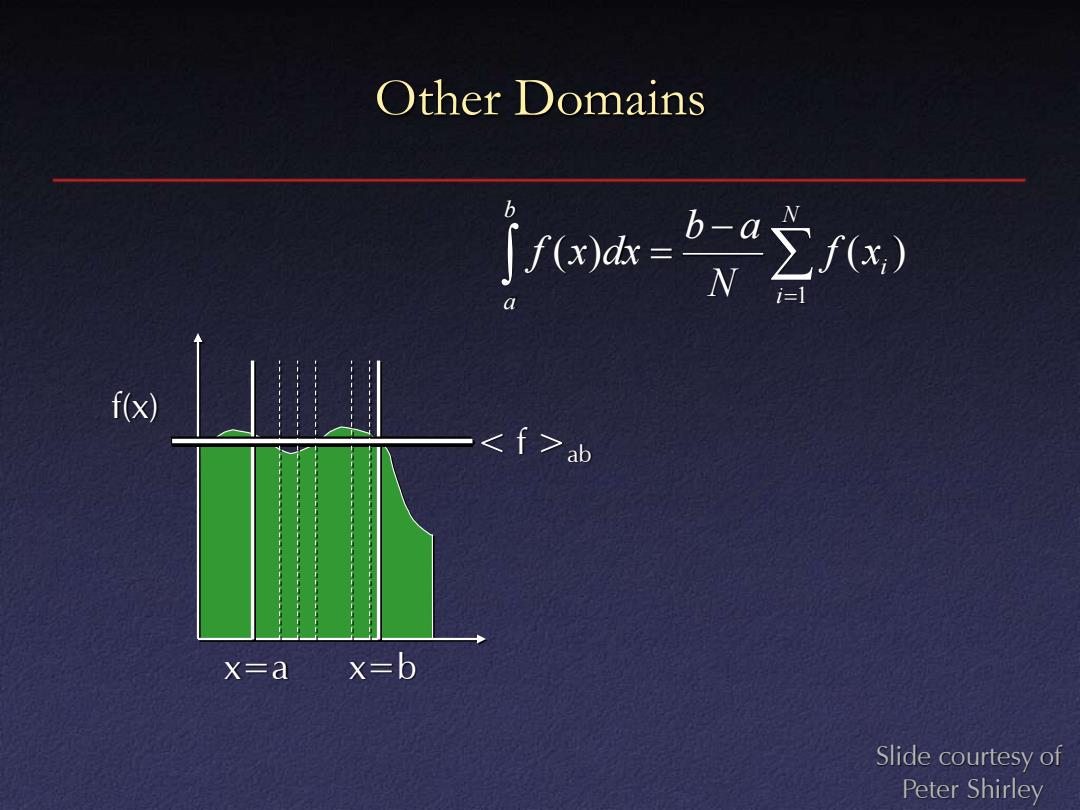
Other Domains jua= i=1 f(x) 一ab X=a x=b Slide courtesy of Peter Shirley
Other Domains x=b f(x) ab x=a = − = N i i b a f x N b a f x dx 1 ( ) ( ) Slide courtesy of Peter Shirley

Benefits of Monte Carlo No "exponential explosion"in required number of samples with increase in dimension Resistance to badly-behaved functions
Benefits of Monte Carlo • No “exponential explosion” in required number of samples with increase in dimension • Resistance to badly-behaved functions
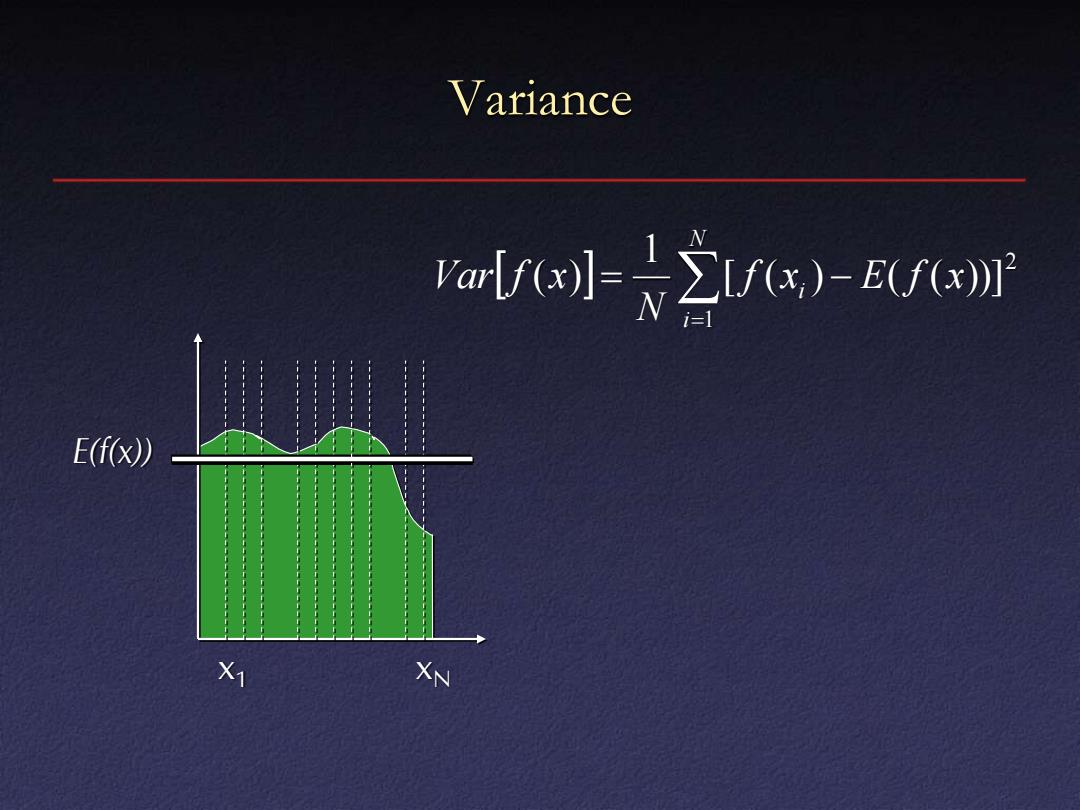
Variance ar/e-∑rx)-/enr E(f(x)) X1 XN
Variance x1 xN E(f(x)) 2 1 [ ( ) ( ( ))] 1 ( ) f x E f x N Var f x N i = i − =
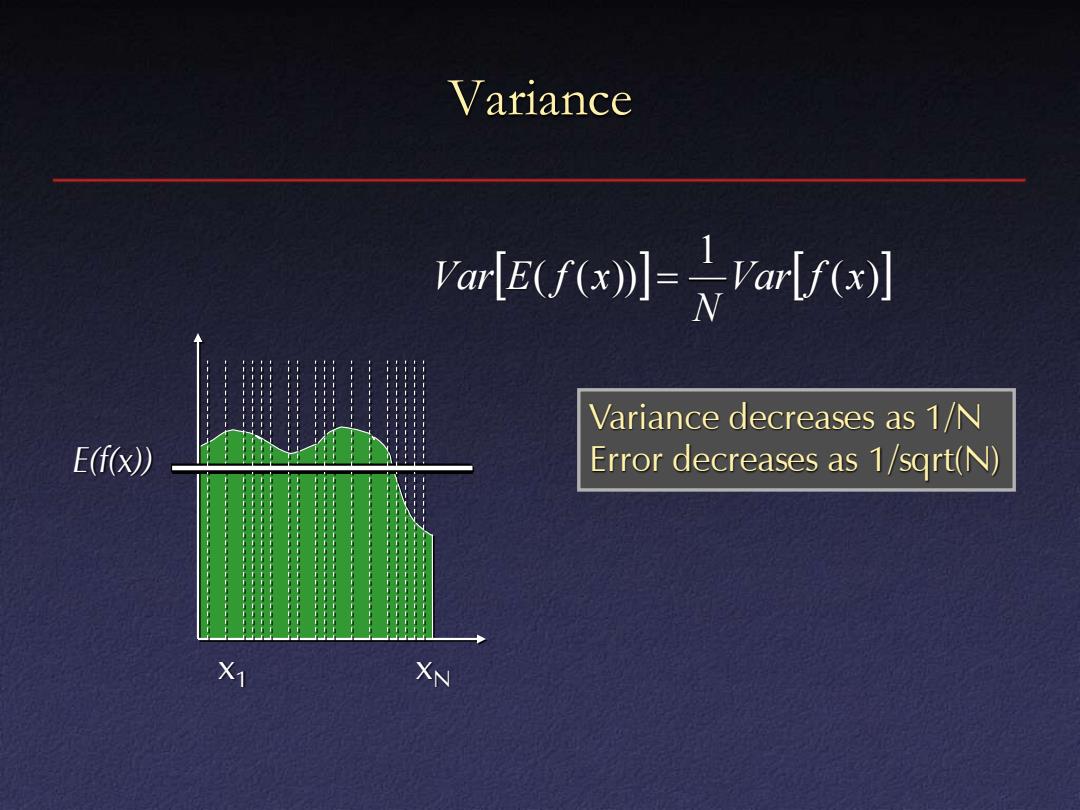
Variance Vara( Variance decreases as 1/N E(f(x)) Error decreases as 1/sqrt(N) X1 XN
Variance x1 xN E(f(x)) ( ) 1 ( ( )) Var f x N Var E f x = Variance decreases as 1/N Error decreases as 1/sqrt(N)
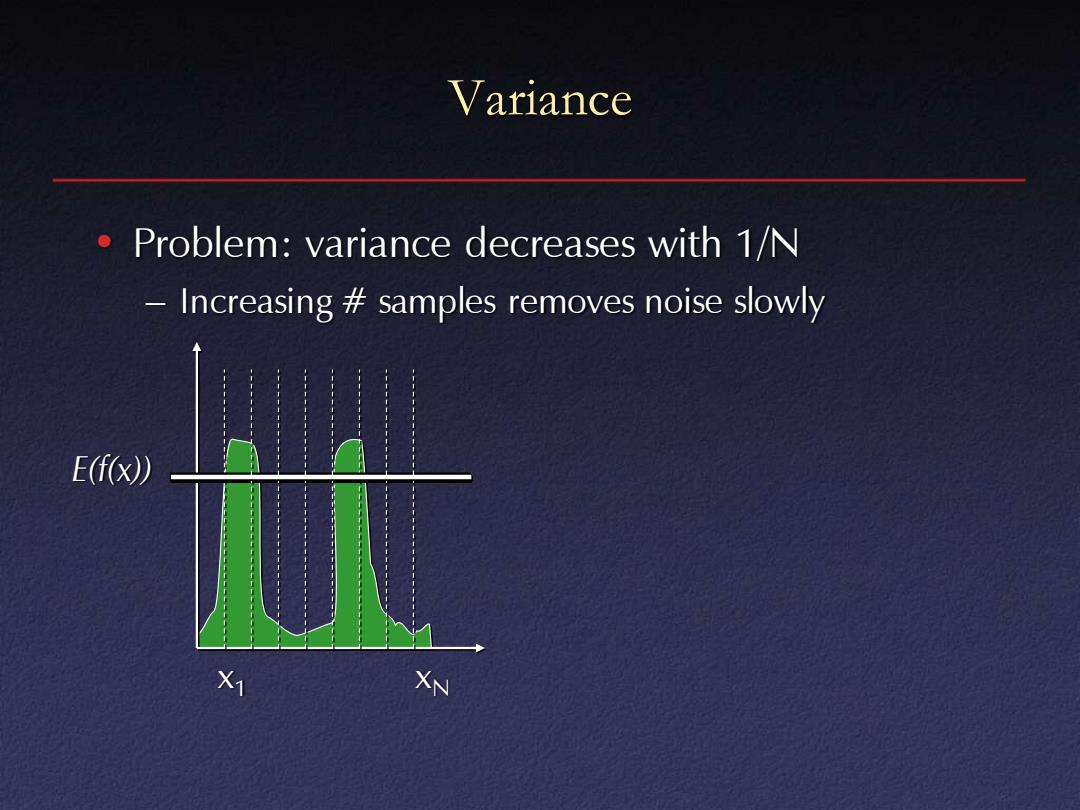
Variance Problem:variance decreases with 1/N Increasing samples removes noise slowly E(f(x)) X1 XN
Variance • Problem: variance decreases with 1/N – Increasing # samples removes noise slowly x1 xN E(f(x))