
第四节 第四章 有理益数的积马 ·基本积分法:直接积分法;换元积分法; 分部积分法 求导 。初等函数 初等函数 积分 本节内容: 一、有理函数的积分 二、可化为有理函数的积分举例
第四节 • 基本积分法 : 换元积分法 ; 分部积分法 • 初等函数 求导 初等函数 积分 一、有理函数的积分 二、可化为有理函数的积分举例 有理函数的积分 本节内容: 第四章 直接积分法 ;

一、有理函数的积分 有理函数: R(x) P() aox”☐axn0 an O(x) box"Obx"Ob m☐n时,R(x)为假分式,mUn时,R(x)为真分式 有理函数 相除 多项式十真分式 分解 若干部分分式之和 其中部分分式的形式为 Mx口N (x20px☐g (kDNP,p2☐4g☐0)) (x☐a)A
一、 有理函数的积分 有理函数: 时, 为假分式; 时, 为真分式 有理函数 相除 多项式 + 真分式 分解 其中部分分式的形式为 若干部分分式之和

有理函数化为部分分式之和的一般规律: (1)分母中若有因式(x-a),则分解后为 A (x-a) x-a 其中4,A,L,A是常数 如 x-3 x-3 (x-1)(x2-1) (x-1(x+1) A B (0x-102 x-
有理函数化为部分分式之和的一般规律: (1)分母中若有因式 ,则分解后为

(2)分母中若有因式(x2+px+q),其中 p2-4g<0则分解后为 Mx+N M,x+N, +2x++2x+)L+x+》 x2+px+q 其中M,N,(i=1,L,k)都是常数
(2)分母中若有因式 ,其中 则分解后为

四种典型部分分式的积分: 1. -dx口Alnx☐aC 2. (x☐a)1o☐C(n☐1) (x2Opx□q) 3. Mx▣N dx 02xOp 变分子为 ¥(2x□p)aNo Mx☐N px0) 再分项积分 (p2☐4g☐0,n01)
四种典型部分分式的积分: 变分子为 再分项积分

x+3 例1.求 dx. -5x+6 解: x+3 x+3 A B x2-5x+6(x-2)(x-3) x-2 x-3 Qx+3=A(x-3)+B(x-2), x+3=(A+B)x-(3A+2B) ìA+B=1, -3A+2B)=3.b4二-J 1B=6 x+3 -5 .6 x2-5x+6x-2x-3
例1. 求 解:
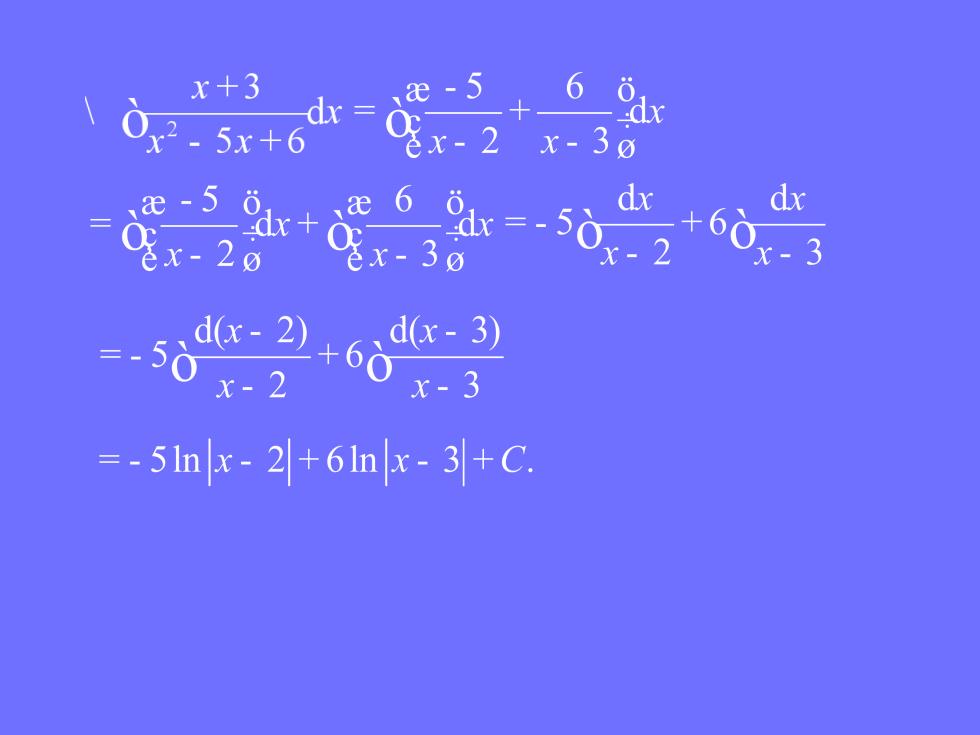
x+3 dx= -5 05x+6 + 含xr-2 6%x x-30 、e-561 6_x=-50x-2 、e6 dx dx 0x-20 x-3g 60 -3 0g6 =50 x-2 =-5In x-2+6Inx-3+C

x+2 例2.求 02x+12+x+ dx. 解: x+2 Bx+D (2x+1)(x2+x+1) 2x+1 x2+x+1 A=(2x+1)原式 x+2 x=. =2 x2+x+1 分别令x☐0,1代入等式两端 2=2+D 32,B+D 一{ 3 3 x+2 2 (2x+I)(x2+x+I)2x+1x2+x+1
例2. 求 解:

x+2 、e2 2r+1+x+- 02x+1x2+x+10 =02xddg+x+ x2+x+1 dx 2+x+1 -al2+m++D吃e dx arctan 2x+1 FC

x-3 例3.求 dx-108- dx. 解: x-3 x-3 B (x-1)x2-1)(x-)(x+1) (x-1)2 x-1 x十1 |D=*)源式 x-3 (x-1)2x=-1 =-1 分别令x=0,2代入等式两端 -3=A-B-1 =A+B.月 B=1 3 x-3 11 (x-10(x2-1)(x-1)2x-1x+1
例3. 求 解: