
第二节 数列的极限 一、数列极限的概念 二、收敛数列的性质
二、 收敛数列的性质 一 、数列极限的概念 第二节 数列的极限

数列极限的概念 (一) 引例 (二) 数列极很的定义
一、数列极限的概念 (一) 引例 (二) 数列极限的定义

(一)引例 1.求半径为r的 圆的面积S 作圆的内接正多边形 正三角形:S 正六边形:
(一)引例 求半径为r的 圆的面积S 1. 作圆的内接正多边形 正三角形:S1 正六边形:

(一)引例 1.求半径为r的 圆的面积S 作圆的内接正多边形 正三角形:S 正六边形:S2
(一)引例 求半径为r的 圆的面积S 1. 作圆的内接正多边形 正三角形:S1 正六边形:S2
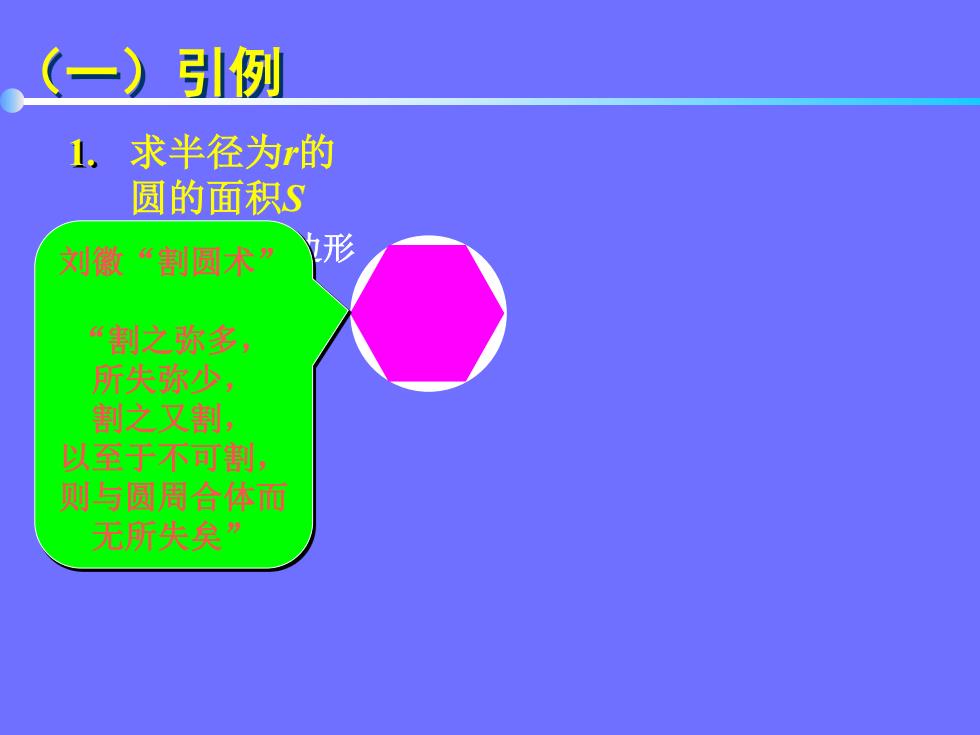
(一)引例 1.求半径为r的 圆的面积S 刘徽“割圆术” 形 “割之弥多, 所失弥少, 割之又割, 以至于不可割, 则与圆周合体而 无所失矣
(一)引例 求半径为r的 圆的面积S 1. 作圆的内接正多边形 正三角形:S1 正六边形:S2 正十二边形:S3 . Sn 当n无限增大时 Sn的变化趋势为S 越 来 越 接 近 S 越 来 越 接 近 S 刘徽“割圆术” “割之弥多, 所失弥少, 割之又割, 以至于不可割, 则与圆周合体而 无所失矣
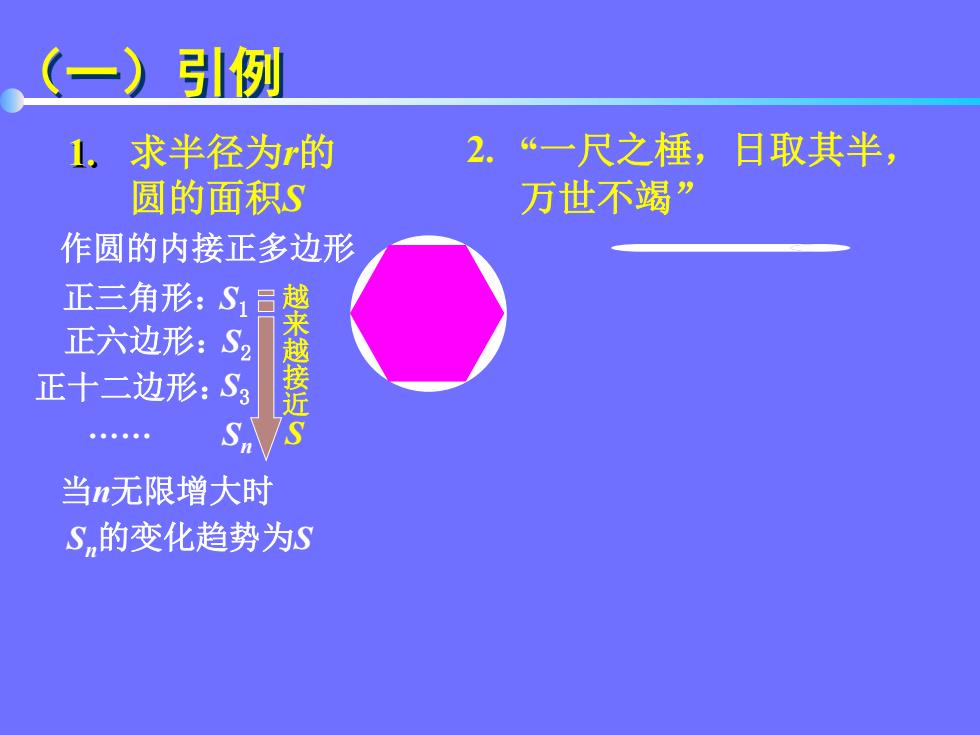
(一)引例 1.求半径为r的 2.“一尺之棰,日取其半, 圆的面积S 万世不竭” 作圆的内接正多边形 三角形: 正六边形:S2 越 正十二边形:S3 . S 当n无限增大时 Sn的变化趋势为S
(一)引例 求半径为r的 圆的面积S 1. 作圆的内接正多边形 正三角形:S1 正六边形:S2 正十二边形:S3 . Sn 当n无限增大时 Sn的变化趋势为S “一尺之棰,日取其半, 万世不竭” 2. 越 来 越 接 近 S
(一)引例 1.求半径为r的 2.“一尺之棰,日取其半, 圆的面积S 万世不竭” 作圆的内接正多边形 正三角形:S1 正六边形:S2 来 正十二边形:S3 当n无限增大时 Sn的变化趋势为S
(一)引例 求半径为r的 圆的面积S 1. 作圆的内接正多边形 正三角形:S1 正六边形:S2 正十二边形:S3 . Sn 当n无限增大时 Sn的变化趋势为S “一尺之棰,日取其半, 万世不竭” 2. 越 来 越 接 近 S
(一)引例 1.求半径为r的 2.“一尺之棰,日取其半, 圆的面积S 万世不竭” 作圆的内接正多边形 三角形: 正六边形:S2 越 正十二边形:S3 S 当n无限增大时 Sn的变化趋势为S
(一)引例 求半径为r的 圆的面积S 1. 作圆的内接正多边形 正三角形:S1 正六边形:S2 正十二边形:S3 . Sn 当n无限增大时 Sn的变化趋势为S “一尺之棰,日取其半, 万世不竭” 2. 越 来 越 接 近 S
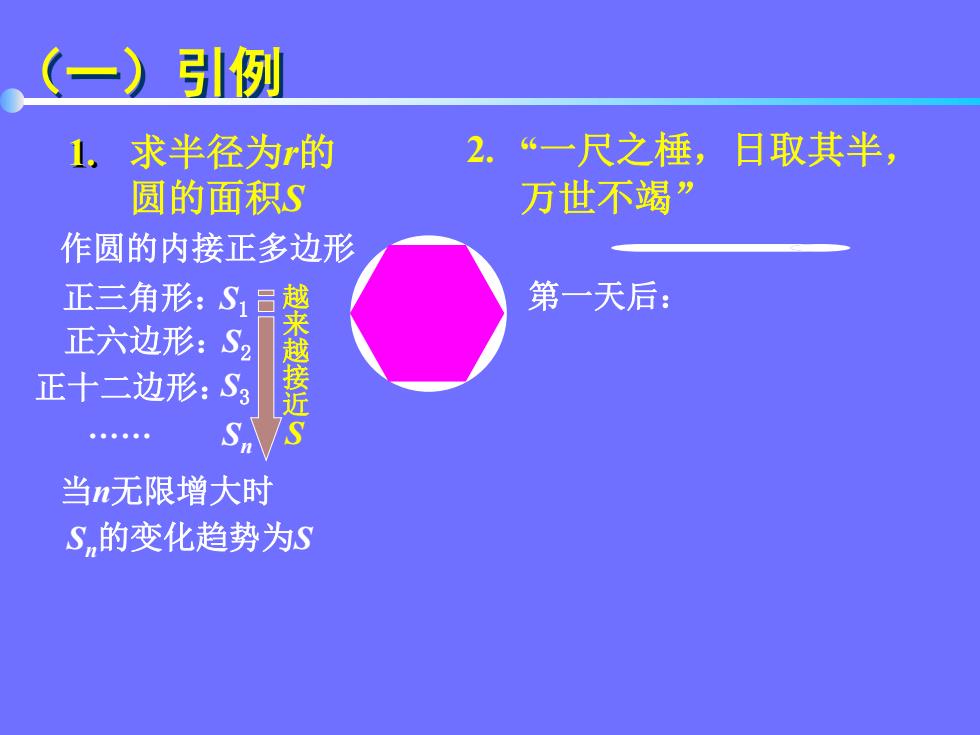
(一)引例 1.求半径为r的 2.“一尺之棰, 日取其半, 圆的面积S 万世不竭” 作圆的内接正多边形 正三角形:S1 第一天后: 正六边形:S2 来 正十二边形:S3 S 当n无限增大时 Sn的变化趋势为S
(一)引例 求半径为r的 圆的面积S 1. 作圆的内接正多边形 正三角形:S1 正六边形:S2 正十二边形:S3 . Sn 当n无限增大时 Sn的变化趋势为S “一尺之棰,日取其半, 万世不竭” 2. 越 第一天后: 来 越 接 近 S
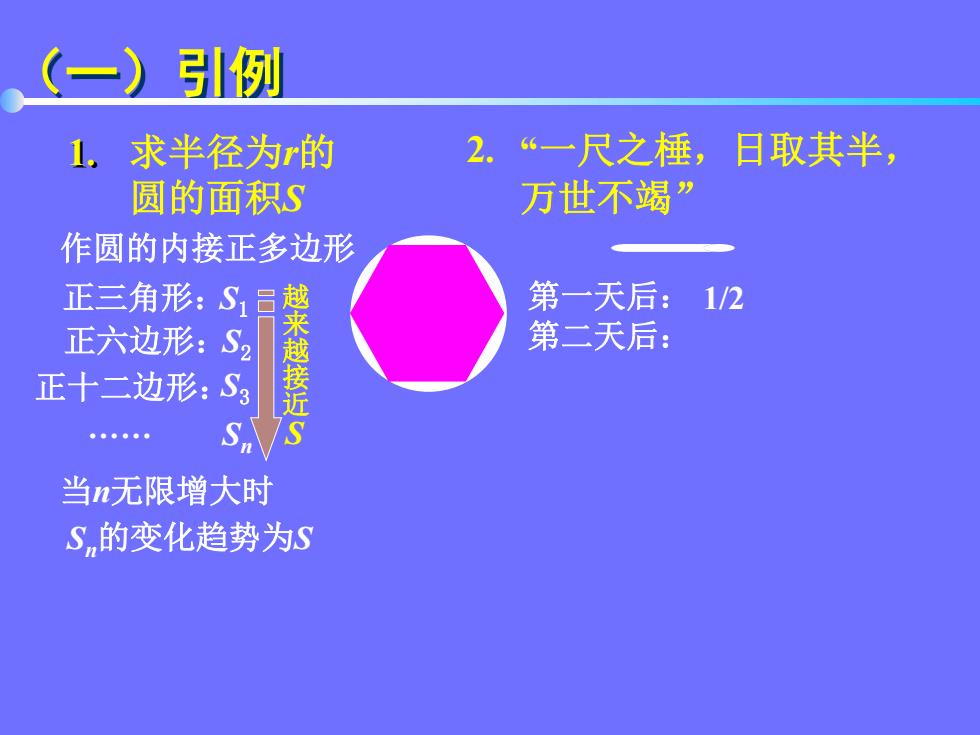
(一)引例 1.求半径为r的 2. “一尺之棰,日取其半, 圆的面积S 万世不竭” 作圆的内接正多边形 三角形: 第一天后:1/2 正六边形:S2 越 第二天后: 正十二边形:S3 近 当n无限增大时 Sn的变化趋势为S
(一)引例 求半径为r的 圆的面积S 1. 作圆的内接正多边形 正三角形:S1 正六边形:S2 正十二边形:S3 . Sn 当n无限增大时 Sn的变化趋势为S “一尺之棰,日取其半, 万世不竭” 2. 第一天后: 1/2 第二天后: 越 来 越 接 近 S