
第七节 第三章 平面曲线的曲率 主要内容: 一、 弧微分 二、 曲率及其计算公式 三、曲率圆与曲率半径
第七节 主要内容: 一、 弧微分 二、 曲率及其计算公式 三、 曲率圆与曲率半径 平面曲线的曲率 第三章

一、 弧微分 设y口f(x)在(a,b)内有连续导数,y y f(x)
一、 弧微分 设 在(a , b)内有连续导数
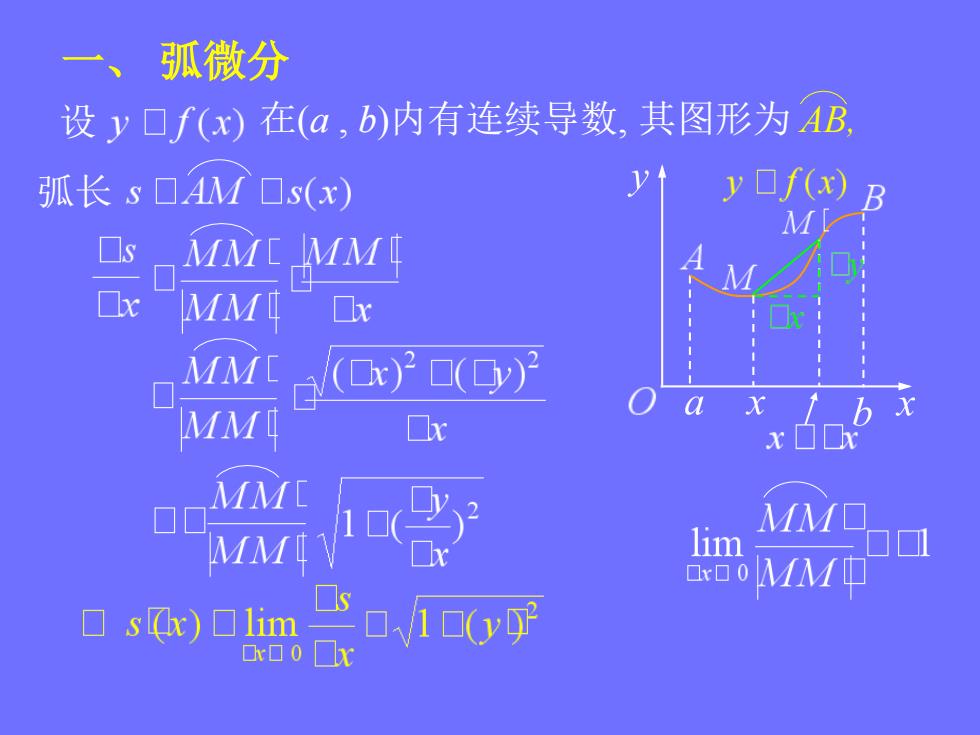
一、弧微分 设y口f(x)在(a,b)内有连续导数,其图形为AB 弧长s口AM口s(x) (0x)(y)2 MM lim oMM 0sx)口lim 0V1(y xa0□x
一、 弧微分 设 在(a , b)内有连续导数, 其图形为 AB, 弧长

sx)CV1□(y0 口ds口V1☐ydx或ds口V(dx)2☐(dy) 若曲线由参数方程表示 则弧长微分公式为 几何意义: ds EMT 1 xx☐dx
则弧长微分公式为 或 几何意义: 若曲线由参数方程表示:
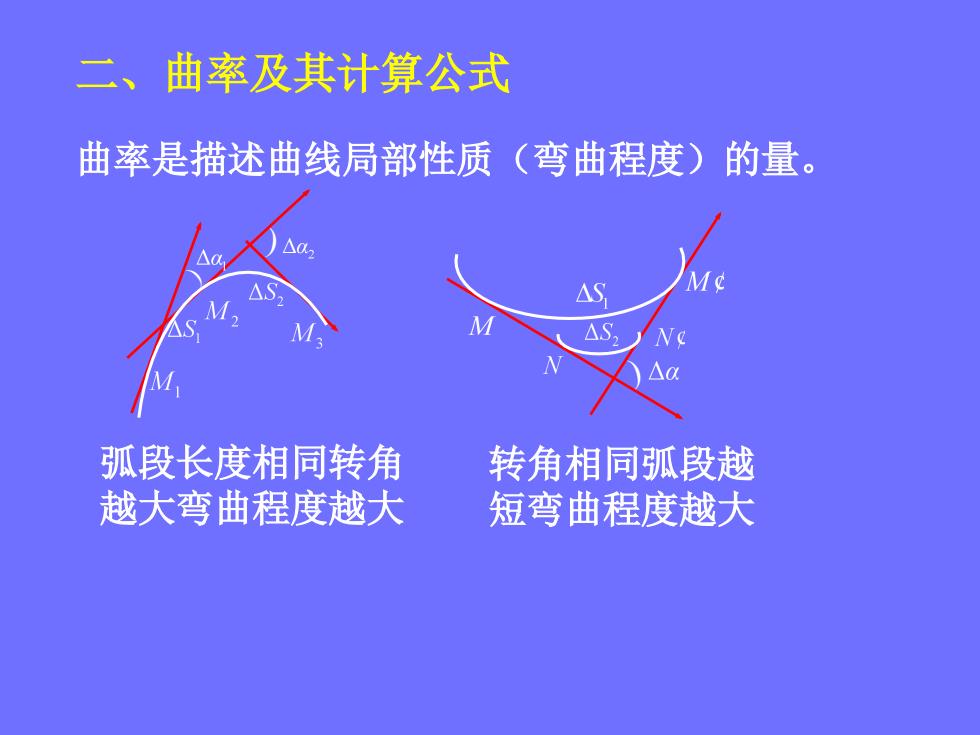
二、曲率及其计算公式 曲率是描述曲线局部性质(弯曲程度)的量。 弧段长度相同转角 转角相同弧段越 越大弯曲程度越大 短弯曲程度越大
二、曲率及其计算公式 曲率是描述曲线局部性质(弯曲程度)的量。 ) ) 弧段长度相同转角 越大弯曲程度越大 转角相同弧段越 短弯曲程度越大 )
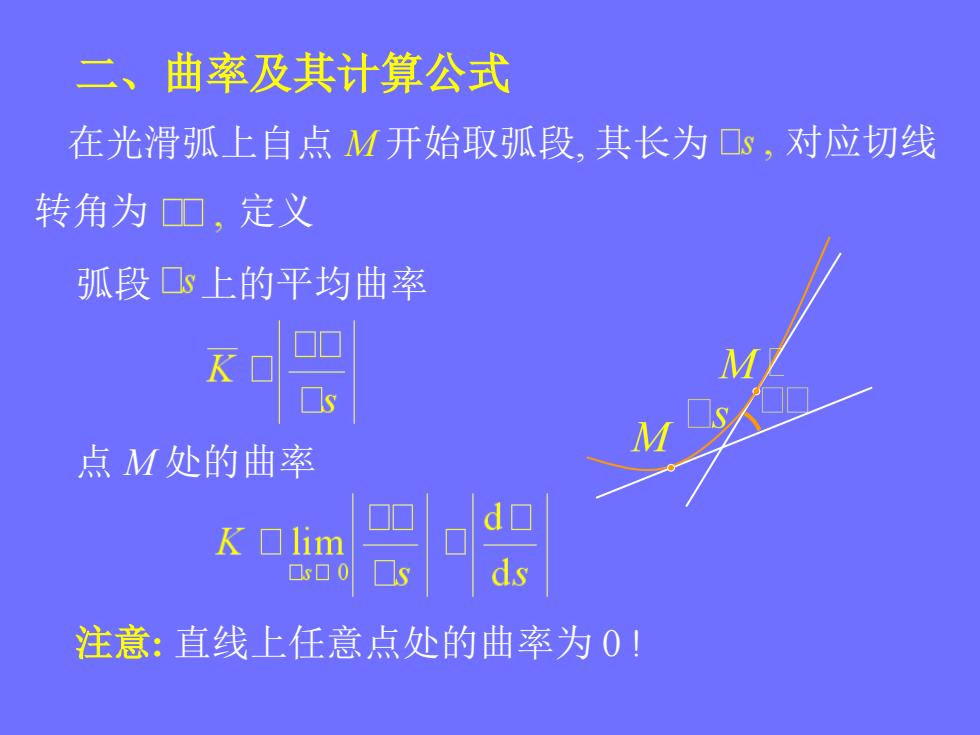
二、曲率及其计算公式 在光滑弧上自点M开始取弧段,其长为Cs,对应切线 转角为D,定义 弧段s上的平均曲率 ■ 点M处的曲率 Klim 0s▣0 注意:直线上任意点处的曲率为0!
二、曲率及其计算公式 在光滑弧上自点 M 开始取弧段, 其长为 对应切线 定义 弧段 上的平均曲率 点 M 处的曲率 注意: 直线上任意点处的曲率为 0 ! 转角为

例1.求半径为R的圆上任意点处的曲率 解:如图所示, Is ORO□ ▣K▣lim 0s▣0 R 可见:R愈小,则K愈大,圆弧弯曲得愈厉害; R愈大,则K愈小,圆弧弯曲得愈小
例1. 求半径为R 的圆上任意点处的曲率 . 解: 如图所示 , 可见: R 愈小, 则K 愈大 , 圆弧弯曲得愈厉害 ; R 愈大, 则K 愈小 , 圆弧弯曲得愈小

曲率K的计算公式 K 设曲线弧y口f(x)二阶可导,则由 ds am1(设吸受 得 ▣☐arctan yl d0(aretany口,_y0 Iyd 又 ds☐1☐ydx 故曲率计算公式为 y中 (1Oya为 当y中卫1时,有曲率近似计算公式K回y①
有曲率近似计算公式 故曲率计算公式为 又 曲率K 的计算公式 设曲线弧 二阶可导, 则由

说明: (1)若曲线由参数方程 给出,则 (2)若曲线方程为x□☐(y),则 K x中 (1☐x3)为 K y四 (1☐y☑)%
说明: (1) 若曲线由参数方程 给出, 则 (2) 若曲线方程为 则

例2. 解 yo2ax+b,yo=2a, \k= 2a [1+(2ax+b)2]3 显然,当x=- 时,最大 2a 又Q( b b2-Aac 2a’ 为抛物线的顶点, Aa \抛物线在顶点处的曲率最大
例2. 解 显然