
第12卷第5期 智能系统学报 Vol.12 No.5 2017年10月 CAAI Transactions on Intelligent Systems 0ct.2017 D0I:10.11992/is.201609020 网络出版地址:http:/kns.cmki.net/kcms/detail/23.1538.TP.20170317.1937.006.html 基于高维k-近邻互信息的特征选择方法 周红标12,3,乔俊飞12 (1.北京工业大学信息学部,北京100124:2.计算智能和智能系统北京市重点实验室,北京100124:3.淮阴工学院 自动化学院,江苏淮安223003) 摘要:针对多元序列预测建模过程中特征选择问题,提出了一种基于数据驱动型高维k近邻互信息的特征选择方 法。该方法首先将数据驱动型k近邻法扩展用于高维特征变量之间互信息的估计,然后采用前向累加策略给出全 部特征最优排序,根据预设无关特征个数剔除无关特征,再利用后向交叉策略找出并剔除冗余特征,最终得到最优 强相关特征子集。以riedman数据、Housing数据和实际污水处理出水总磷预测数据为例,采用多层感知器神经网 络预测模型进行仿真实验,验证了所提方法的有效性。 关键词:特征选择:互信息:k近邻:高维互信息:多层感知器 中图分类号:TP183文献标志码:A文章编号:1673-4785(2017)05-0595-06 中文引用格式:周红标,乔俊飞.基于高维k-近邻互信息的特征选择方法[J].智能系统学报,2017,12(5):595-600. 英文引用格式:ZHOU Hongbiao,QIAO Junfei.Feature selection method based on high dimensional-nearest neighbors mutual information[J].CAAI transactions on intelligent systems,2017,12(5):595-600. Feature selection method based on high dimensional k-nearest neighbors mutual information ZHOU Hongbiao2.3,QIAO Junfei (1.Faculty of Information Technology,Beijing University of Technology,Beijing 100124,China;2.Beijing Key Laboratory of Computational Intelligence and Intelligent System,Beijing 100124,China;3.Faculty of Automation,Huaiyin Institute of Technology, Huai'an 223003,China) Abstract:Feature selection plays an important role in the modeling and forecast of multivariate series.In this paper,we propose a feature selection method based on data-driven high-dimensional k-nearest neighbor mutual information.First,this method extends the k-nearest neighbor method to estimate the amount of mutual information among high-dimensional feature variables.Next,optimal sorting of all these features is achieved by adopting a forward accumulation strategy in which irrelevant features are eliminated according to a preset number.Then, redundant features are located and removed using a backward cross strategy.Lastly,this method obtains optimal subsets that feature a strong correlation.Using Friedman data,housing data,and actual effluent total-phosphorus forecast data from wastewater treatment plant as examples,we performed a simulation experiment by adopting a neural network forecast model with multilayer perception.The simulation results demonstrate the feasibility of the proposed method. Keywords:feature selection;mutual information;k-nearest neighbor;high-dimensional mutual information; multilayer perceptron 通过特征选择实现数据降维,构建结构精简的 目前,特征选择的方法主要有偏最小二乘回归 辨识模型,能够有效避免输入特征太多造成“维数 (partial least squares regression,PLSR)[4、灰色关联 灾难”以及给学习模型带来“过拟合”等问题-)。 分析(grey relational analysis,GRA)Is)和互信息 收稿日期:2016-09-21.网络出版日期:2017-03-17. (mutual information,M)[s-刀等。MI对样本的分布 基金项目:国家自然科学基金重点项目(61533002). 类型无特别要求,可有效捕捉特征间的非线性关 通信作者:乔俊飞.E-mail:hyitzhb@163.com. 系,特别适合多元序列特征选择问题
第 12 卷第 5 期 智 能 系 统 学 报 Vol.12 №.5 2017 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2017 DOI:10.11992 / tis.201609020 网络出版地址:http: / / kns.cnki.net / kcms/ detail / 23.1538.TP.20170317.1937.006.html 基于高维 k-近邻互信息的特征选择方法 周红标1,2,3 ,乔俊飞1,2 (1.北京工业大学 信息学部,北京 100124; 2. 计算智能和智能系统北京市重点实验室,北京 100124; 3.淮阴工学院 自动化学院,江苏 淮安 223003) 摘 要:针对多元序列预测建模过程中特征选择问题,提出了一种基于数据驱动型高维 k⁃近邻互信息的特征选择方 法。 该方法首先将数据驱动型 k⁃近邻法扩展用于高维特征变量之间互信息的估计,然后采用前向累加策略给出全 部特征最优排序,根据预设无关特征个数剔除无关特征,再利用后向交叉策略找出并剔除冗余特征,最终得到最优 强相关特征子集。 以 Friedman 数据、Housing 数据和实际污水处理出水总磷预测数据为例,采用多层感知器神经网 络预测模型进行仿真实验,验证了所提方法的有效性。 关键词:特征选择;互信息;k⁃近邻;高维互信息;多层感知器 中图分类号:TP183 文献标志码:A 文章编号:1673-4785(2017)05-0595-06 中文引用格式:周红标,乔俊飞.基于高维 k-近邻互信息的特征选择方法[J]. 智能系统学报, 2017, 12(5): 595-600. 英文引用格式:ZHOU Hongbiao,QIAO Junfei. Feature selection method based on high dimensional k⁃nearest neighbors mutual information[J]. CAAI transactions on intelligent systems, 2017, 12(5): 595-600. Feature selection method based on high dimensional k⁃nearest neighbors mutual information ZHOU Hongbiao 1,2,3 , QIAO Junfei 1,2 (1. Faculty of Information Technology, Beijing University of Technology, Beijing 100124, China; 2. Beijing Key Laboratory of Computational Intelligence and Intelligent System, Beijing 100124, China;3. Faculty of Automation, Huaiyin Institute of Technology, Huai’an 223003, China) Abstract:Feature selection plays an important role in the modeling and forecast of multivariate series. In this paper, we propose a feature selection method based on data⁃driven high⁃dimensional k⁃nearest neighbor mutual information. First, this method extends the k⁃nearest neighbor method to estimate the amount of mutual information among high⁃dimensional feature variables. Next, optimal sorting of all these features is achieved by adopting a forward accumulation strategy in which irrelevant features are eliminated according to a preset number. Then, redundant features are located and removed using a backward cross strategy. Lastly, this method obtains optimal subsets that feature a strong correlation. Using Friedman data, housing data, and actual effluent total⁃phosphorus forecast data from wastewater treatment plant as examples, we performed a simulation experiment by adopting a neural network forecast model with multilayer perception. The simulation results demonstrate the feasibility of the proposed method. Keywords: feature selection; mutual information; k⁃nearest neighbor; high⁃dimensional mutual information; multilayer perceptron 收稿日期:2016-09-21. 网络出版日期 基金项目:国家自然科学基金重点项目(6 : 1 2 5 0 3 1 3 7 0 - 0 0 2 3 ). -17. 通过特征选择实现数据降维,构建结构精简的 辨识模型,能够有效避免输入特征太多造成“ 通信作者:乔俊飞. E⁃mail:hyitzhb@ 163.com. 维数 灾难”以及给学习模型带来“过拟合” 等问题[1-3] 。 目前,特 征 选 择 的 方 法 主 要 有 偏 最 小 二 乘 回 归 (partial least squares regression, PLSR) [4] 、灰色关联 分析 ( grey relational analysis, GRA) [5] 和 互 信 息 (mutual information, MI) [6-7] 等。 MI 对样本的分布 类型无特别要求,可有效捕捉特征间的非线性关 系,特别适合多元序列特征选择问题

·596 智能系统学报 第12卷 互信息是一种衡量两个随机变量之间相互依 H(X)=-px(x)logpx(x)dx (4) 赖强弱程度的准则,其来源于信息论中嫡的概 念劉。采用互信息进行特征选择主要有以下两个 H(Y)=-p(y)logp(y)dy (5) 难点:1)特征评价策略;2)互信息的准确估计。针 对评价策略,Battiti等[]提出了MFS(mutual H(X.Y)=-px.x(x.y)logpx.x(x.y)dxdy(6) information feature selection)方法,通过平衡相关特 根据式(4)、(5)和(6),式(3)还可以表示为 征和冗余特征的选择,取得了较好的效果,此后, I(X;Y)=H(X)+H(Y)-H(X,Y) (7) Peng等o、Fleuret、Yang等Ia、Brown[)和韩 等都分别提出了各自的评价策略。上述方法主 2 高维k-近邻互信息理论 要是采用一维互信息来衡量特征好坏,当存在冗余 2.1 高维k-近邻互信息的估计 特征时,并不能保证得到最优特征子集。互信息的 Kraskov等7-8]提出的k-近邻法通过数据直接 估计一般通过非参数方式[6)求解概率密度函数 近似估计特征的互信息,避免了对概率密度分布的 来实现,主要有直方图法和核函数法。近几年发展 近似估计。其基本思想是,在由随机变量X和Y构 的k-近邻法(k-nearest neighbors,kNN)I-I8]构建的 成的空间中对于给定的N个样本首先找出它的k 数据驱动型特征选择框架,无需假设概率密度函数 个近邻,再找出其他样本分别在X和Y方向到当前 形式,避免了对概率密度函数的估计,其基础理论 样本的距离小于当前样本到k个近邻距离的最大值 完备,非常适合具有非线性不规则分布特点的实际 的数目,通过统计数目从而进行互信息的估计。 数据,但是高维k-近邻互信息的估计存在一定困难。 现将其扩展到高维互信息的估计,高维互信息 因此,本文在k-近邻互信息基础上将其扩展用 计算的具体思路如下8]: 于高维互信息的估计,然后采用前向累加后向交叉 给定N个样本z=[(x)r(y)T]T(i=1, (forward accumulation and backward cross,FABC) 2,…,N),其中x0∈Rd且y0∈RP。如果z和z 最优特征子集选择策略,构建kNN-FABC的特征选 为数据集中两个不同的向量,则 择方法,最后以Friedman数据、Housing数据和实际 ‖z-z'‖=max(‖x-x'I,Iy-y'I)(8) 污水处理出水总磷预测数据为例进行仿真实验,并 式中·【表示取最大范数。 结合多层感知器(multilayer perceptron,MLP)预测 若z⊙的k-近邻为z》=[(x)T(y)T]T, 模型来验证所提特征选择方法的有效性。 则z)与z)之间的Euclidean距离为 e0=‖z0-z)1三 1互信息理论 max((() (9) 互信息是一种衡量两个随机变量之间相互依 对于z)中的分量x0和y0有 赖强弱程度的准则,其来源于信息论中嫡的概念。 e0=-Ir0-xo》‖=maxx0-xo)l 三12, 两个随机变量之间的互信息越大,则两者之间的相 (10) 关性就越强)。 9=0-yo》1=,盟,y9-yo1 对随机变量X和Y来说,设其联合概率密度函 (11) 数为Px.y(x,y),则其边缘概率密度函数为 将与x和y之间距离小于o的样本点个数 ex(x)=exx(x,y)dy (1) 分别记为N和N。因此,变量X和Y之间互信息的 py(y)=Jpx.x(x.y)dx 估计量为 (2) 根据信息论的有关理论[),随机变量X和Y之 i(x:)=k)-d+P-1+(d+p-1)n- k 间的互信息定义为 三(2心)·三) (12) (x:)()og) ()p(ddy (3) 式中:亚(·)为digama函数,(+1)=亚()+, 式中S为X和Y的定义域。 根据Shannon嫡的定义[),X、Y的熵和联合熵 (1)≈-0.5772156:k一般取2~6。通过式(12)可以 分别为 发现,(X:Y)不仅与k和N有关,而且与变量X和Y
互信息是一种衡量两个随机变量之间相互依 赖强弱 程 度 的 准 则, 其 来 源 于 信 息 论 中 熵 的 概 念[8] 。 采用互信息进行特征选择主要有以下两个 难点:1)特征评价策略;2) 互信息的准确估计。 针 对评 价 策 略, Battiti 等[9] 提 出 了 MIFS ( mutual information feature selection) 方法,通过平衡相关特 征和冗余特征的选择,取得了较好的效果,此后, Peng 等[10] 、 Fleuret [11] 、 Yang 等[12] 、 Brown [13] 和 韩 等[14]都分别提出了各自的评价策略。 上述方法主 要是采用一维互信息来衡量特征好坏,当存在冗余 特征时,并不能保证得到最优特征子集。 互信息的 估计一般通过非参数方式[15-16] 求解概率密度函数 来实现,主要有直方图法和核函数法。 近几年发展 的 k⁃近邻法(k⁃nearest neighbors, kNN) [17-18] 构建的 数据驱动型特征选择框架,无需假设概率密度函数 形式,避免了对概率密度函数的估计,其基础理论 完备,非常适合具有非线性不规则分布特点的实际 数据,但是高维 k⁃近邻互信息的估计存在一定困难。 因此,本文在 k⁃近邻互信息基础上将其扩展用 于高维互信息的估计,然后采用前向累加后向交叉 (forward accumulation and backward cross, FABC)的 最优特征子集选择策略,构建 kNN⁃FABC 的特征选 择方法,最后以 Friedman 数据、Housing 数据和实际 污水处理出水总磷预测数据为例进行仿真实验,并 结合多层感知器(multilayer perceptron, MLP) 预测 模型来验证所提特征选择方法的有效性。 1 互信息理论 互信息是一种衡量两个随机变量之间相互依 赖强弱程度的准则,其来源于信息论中熵的概念。 两个随机变量之间的互信息越大,则两者之间的相 关性就越强[17] 。 对随机变量 X 和 Y 来说,设其联合概率密度函 数为 ρX,Y(x,y) ,则其边缘概率密度函数为 ρX(x) = ∫ρX,Y(x,y)dy (1) ρY(y) = ∫ρX,Y(x,y)dx (2) 根据信息论的有关理论[17] ,随机变量 X 和 Y 之 间的互信息定义为 I(X;Y) = ∬ S ρX,Y(x,y)log ρX,Y(x,y) ρX(x)ρY(y) dxdy (3) 式中 S 为 X 和 Y 的定义域。 根据 Shannon 熵的定义[17] ,X、Y 的熵和联合熵 分别为 H(X) = - ∫ρX(x)log ρX(x)dx (4) H(Y) = - ∫ρY(y)log ρY(y)dy (5) H(X,Y) = - ∬ S ρX,Y(x,y)log ρX,Y(x,y)dxdy (6) 根据式(4)、(5)和(6),式(3)还可以表示为 I(X;Y) = H(X) + H(Y) - H(X,Y) (7) 2 高维 k⁃近邻互信息理论 2.1 高维 k⁃近邻互信息的估计 Kraskov 等[17-18]提出的 k⁃近邻法通过数据直接 近似估计特征的互信息,避免了对概率密度分布的 近似估计。 其基本思想是,在由随机变量 X 和 Y 构 成的空间中对于给定的 N 个样本首先找出它的 k 个近邻,再找出其他样本分别在 X 和 Y 方向到当前 样本的距离小于当前样本到 k 个近邻距离的最大值 的数目,通过统计数目从而进行互信息的估计。 现将其扩展到高维互信息的估计,高维互信息 计算的具体思路如下[18] : 给定 N 个样本z (i) = [(x (i) ) T (y (i) ) T ] T ( i = 1, 2,…,N) ,其中 x (i) ∈ℝ d 且 y (i) ∈ℝ p 。 如果 z 和 z′ 为数据集中两个不同的向量,则 ‖z - z′‖ = max(‖x - x′‖,‖y - y′‖) (8) 式中‖·‖表示取最大范数。 若z (i) 的k⁃近邻为 z (k(i)) = [(x (k(i)) ) T (y (k(i)) ) T ] T , 则 z (i) 与 z (k(i)) 之间的 Euclidean 距离为 ε (i) = ‖ z (i) - z (k(i))‖ = max(‖x (i) - x (k(i))‖,‖y (i) - y (k(i))‖) (9) 对于 z (i) 中的分量 x (i) 和 y (i) 有 ε (i) x = ‖x (i) - x (k(i))‖ = max s = 1,2,…,d x (i) s - x (k(i)) s (10) ε (i) y = ‖y (i) - y (k(i))‖ = max t = 1,2,…,p y (i) t - y (k(i)) t (11) 将与 x (i) s 和 y (i) t 之间距离小于 ε (i)的样本点个数 分别记为N (i) xs 和N (i) yt 。 因此,变量X 和Y 之间互信息的 估计量为 I ^ (X;Y) = Ψ(k) - d + p - 1 k + (d + p - 1)Ψ(N) - 1 N∑ N p = 1 ∑ d s = 1 Ψ(N (i) xs ) + ∑ p t = 1 Ψ(N (i) yt ( )) (12) 式中:Ψ(·)为 digamma 函数,Ψ(t +1) = Ψ(t) + 1 t , Ψ(1)≈-0.577 215 6; k 一般取 2~6。 通过式(12)可以 发现, I ^ (X;Y) 不仅与 k 和 N 有关,而且与变量 X 和 Y ·596· 智 能 系 统 学 报 第 12 卷
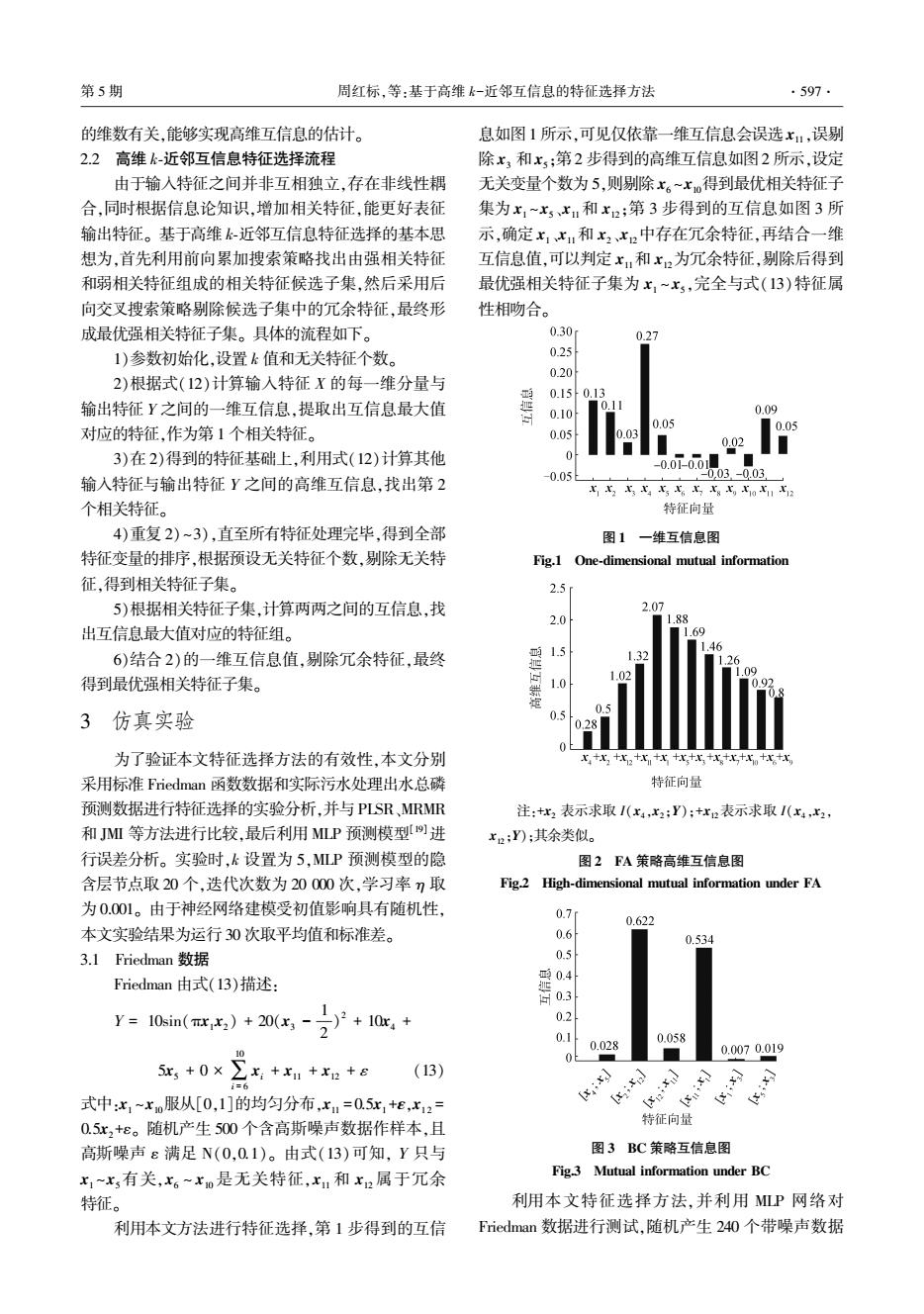
第5期 周红标,等:基于高维k-近邻互信息的特征选择方法 .597. 的维数有关,能够实现高维互信息的估计。 息如图1所示,可见仅依靠一维互信息会误选x1,误别 2.2高维k-近邻互信息特征选择流程 除x,和x:第2步得到的高维互信息如图2所示,设定 由于输入特征之间并非互相独立,存在非线性耦 无关变量个数为5,则剔除x。~x。得到最优相关特征子 合,同时根据信息论知识,增加相关特征,能更好表征 集为x,~xx,和x2;第3步得到的互信息如图3所 输出特征。基于高维k-近邻互信息特征选择的基本思 示,确定x1x,和x2x2中存在冗余特征,再结合一维 想为,首先利用前向累加搜索策略找出由强相关特征 互信息值,可以判定x,和x2为冗余特征,别除后得到 和弱相关特征组成的相关特征候选子集,然后采用后 最优强相关特征子集为x,~x,完全与式(13)特征属 向交叉搜索策略剔除候选子集中的冗余特征,最终形 性相吻合。 成最优强相关特征子集。具体的流程如下。 0.30 0.27 1)参数初始化,设置k值和无关特征个数。 0.25 0.20 2)根据式(12)计算输入特征X的每一维分量与 0.15 0.13 输出特征Y之间的一维互信息,提取出互信息最大值 0.10 0.09 0.05 对应的特征,作为第1个相关特征。 0.05 0.05 3)在2)得到的特征基础上,利用式(12)计算其他 -0.0i-00 0052 0.03.-0.03 输入特征与输出特征Y之间的高维互信息,找出第2 xx x5o112 个相关特征。 特征向量 4)重复2)~3),直至所有特征处理完毕,得到全部 图1一维互信息图 特征变量的排序,根据预设无关特征个数,剔除无关特 Fig.1 One-dimensional mutual information 征,得到相关特征子集。 2.5 5)根据相关特征子集,计算两两之间的互信息,找 2.07 2.0 ■1.88 出互信息最大值对应的特征组。 ■1.69 1.5 1.46 6)结合2)的一维互信息值,剔除冗余特征,最终 1.32 16 得到最优强相关特征子集。 1.02 1.0 0 3仿真实验 0.5 0.28 为了验证本文特征选择方法的有效性,本文分别 x比+比2+r,+x+r+xx+比+x+xtx 采用标准Friedman函数数据和实际污水处理出水总磷 特征向量 预测数据进行特征选择的实验分析,并与PLSR,MRMR 注:+2表示求取I(x4,x2;Y):+x2表示求取I(x4,x2, 和MI等方法进行比较,最后利用MLP预测模型进 x2;Y);其余类似。 行误差分析。实验时,k设置为5,MLP预测模型的隐 图2FA策略高维互信息图 含层节点取20个,迭代次数为20000次,学习率7取 Fig.2 High-dimensional mutual information under FA 为0.001。由于神经网络建模受初值影响具有随机性, 0.7d 0.622 本文实验结果为运行30次取平均值和标准差。 0.6 0.534 3.1 Friedman数据 0.5 Friedman由式(13)描述: 0.4 问03 y=10sin(mxx,)+20(x3-7)°+10c+ 0.2 0.1 0.028 0.058 5x,+0×∑x+x,+x2+e 0.0070.019 (13) i=6 式中:x1~xo服从[0,1]的均匀分布,x1=0.5x,+e,x12= [x:xj 0.5x2+ε。随机产生500个含高斯噪声数据作样本,且 特征向量 高斯噪声ε满足N(0,0.1)。由式(13)可知,Y只与 图3BC策略互信息图 x1~x有关,x6~xo是无关特征,x1和x2属于冗余 Fig.3 Mutual information under BC 特征。 利用本文特征选择方法,并利用MP网络对 利用本文方法进行特征选择,第1步得到的互信 Friedman数据进行测试,随机产生240个带噪声数据
的维数有关,能够实现高维互信息的估计。 2.2 高维 k⁃近邻互信息特征选择流程 由于输入特征之间并非互相独立,存在非线性耦 合,同时根据信息论知识,增加相关特征,能更好表征 输出特征。 基于高维 k⁃近邻互信息特征选择的基本思 想为,首先利用前向累加搜索策略找出由强相关特征 和弱相关特征组成的相关特征候选子集,然后采用后 向交叉搜索策略剔除候选子集中的冗余特征,最终形 成最优强相关特征子集。 具体的流程如下。 1)参数初始化,设置 k 值和无关特征个数。 2)根据式(12)计算输入特征 X 的每一维分量与 输出特征 Y 之间的一维互信息,提取出互信息最大值 对应的特征,作为第 1 个相关特征。 3)在 2)得到的特征基础上,利用式(12)计算其他 输入特征与输出特征 Y 之间的高维互信息,找出第 2 个相关特征。 4)重复 2) ~3),直至所有特征处理完毕,得到全部 特征变量的排序,根据预设无关特征个数,剔除无关特 征,得到相关特征子集。 5)根据相关特征子集,计算两两之间的互信息,找 出互信息最大值对应的特征组。 6)结合 2)的一维互信息值,剔除冗余特征,最终 得到最优强相关特征子集。 3 仿真实验 为了验证本文特征选择方法的有效性,本文分别 采用标准 Friedman 函数数据和实际污水处理出水总磷 预测数据进行特征选择的实验分析,并与 PLSR、MRMR 和 JMI 等方法进行比较,最后利用 MLP 预测模型[19]进 行误差分析。 实验时,k 设置为 5,MLP 预测模型的隐 含层节点取 20 个,迭代次数为 20 000 次,学习率 η 取 为 0.001。 由于神经网络建模受初值影响具有随机性, 本文实验结果为运行 30 次取平均值和标准差。 3.1 Friedman 数据 Friedman 由式(13)描述: Y = 10sin(πx1x2) + 20(x3 - 1 2 ) 2 + 10x4 + 5x5 + 0 × ∑ 10 i = 6 xi + x11 + x12 + ε (13) 式中:x1 ~x10服从[0,1]的均匀分布,x11 = 0.5x1 +ε,x12 = 0.5x2 +ε。 随机产生 500 个含高斯噪声数据作样本,且 高斯噪声 ε 满足 N(0,0.1)。 由式(13)可知, Y 只与 x1 ~x5有关,x6 ~ x10 是无关特征,x11 和 x12 属于冗余 特征。 利用本文方法进行特征选择,第 1 步得到的互信 息如图1 所示,可见仅依靠一维互信息会误选 x11,误剔 除 x3 和x5;第2 步得到的高维互信息如图2 所示,设定 无关变量个数为 5,则剔除 x6 ~x10得到最优相关特征子 集为 x1 ~x5、x11和 x12;第 3 步得到的互信息如图 3 所 示,确定 x1、x11和 x2、x12中存在冗余特征,再结合一维 互信息值,可以判定 x11和 x12为冗余特征,剔除后得到 最优强相关特征子集为 x1 ~ x5,完全与式(13)特征属 性相吻合。 图 1 一维互信息图 Fig.1 One⁃dimensional mutual information 注:+x2 表示求取 I(x4,x2;Y);+x12表示求取 I(x4,x2, x12;Y);其余类似。 图 2 FA 策略高维互信息图 Fig.2 High⁃dimensional mutual information under FA 图 3 BC 策略互信息图 Fig.3 Mutual information under BC 利用本文特征选择方法,并利用 MLP 网络对 Friedman 数据进行测试,随机产生 240 个带噪声数据 第 5 期 周红标,等:基于高维 k-近邻互信息的特征选择方法 ·597·
·598 智能系统学报 第12卷 作训练样本,1000个不含噪声数据作测试样本,变量 由表2可知,在归一化方法MP模型参数选取一 选择及网络测试结果如表1所示。 致的情况下,kNN-FABC的RMSE均值和标准差均表 表1 Friedman数据特征选择及测试结果 明了采用本文方法所选特征建立的预测模型精度 Table 1 Feature selection and test results for Friedman 更高。 方法 变量选择结果 RMSE 33污水处理出水总磷预测数据 ALL x1-r2 3.101±1.274 近年来,总磷(total phosphorus,TP)污染问题开始 PLSR r4,r2,r1,x5,r11,r2 3.543±1.440 凸显。研究表明,水体富营养化程度与总磷等指标密 MIFS(] x4,x2,r1,x5,r6 2.002±0.095 切相关。因此加强对P的检测有助于解决水体富营 养化问题。目前,污水处理厂普遍采用的生化方法 MRMR(H0] r4r2,x1x56 2.002±0.095 成本高、耗时长,在线检测仪表对检测环境要求高并且 CMIMI] x4,x2,1,x5x6 2.002±0.095 维护成本昂贵,而基于数据驱动的软测量技术能够在 JMIt2) xaxz:x1X5,XR 3.854±1.611 线、快速、准确预测,受到研究者青睐。但是污水处理 MM因 X,X2x1x5XR 3.854±1.611 生化反应过程中可测变量较多,在建立TP软测量模型 STEP(41 X4x2x1x5X3 1.143±0.070 时,若选取全部可用特征,则会产生冗余,降低网络泛 kNN-FABC 4,x2,x1,x5r3 1.143±0.070 化能力,同时也大幅增加检测成本,故对P预测模型 注:ALL表示选取全部特征。 进行输入特征选择具有重要意义。污水处理生化反应 由表1可知,kNN-FABC方法和文献[I7]的STEP 过程中可测变量及其意义如表3所示。本文采用 方法都成功筛选出全部仅有的5个相关特征,MRMR、 kNN-FABC方法实现对TP预测特征变量的选择。 CMM和MFS误别相关特征x3、误选无关特征x6,JM 表3可测变量的意义 和MMI误剔相关特征x3、误选冗余特征x2,PISR误 Table 3 Significance of measurable variables 选冗余特征x,和x2。同时,kNN-FABC方法的RMSE 标记 参数 意义 单位 取样点 均值和标准差都要远小于其他方法,表明其极大地提 T 水温 ℃ 厌氧池 高了网络泛化能力。 3.2 Housing数据 ORP, 氧化还原电位 mV 厌氧池 Housing数据由13个房屋属性的输入特征和1个 D01 溶解氧浓度 mg/L 好氧前端 房屋价格的输出特征组成,共有506组样本。随机选 D02 溶解氧浓度 mg/L 好氧末端 择338组作训练样本,剩余168组作测试样本。利用本 文方法进行特征选择,并与其他文献特征选择结果进 TSS 总固体悬浮物浓度 g/L 好氧末端 行了比较,特征选择及MLP网络测试结果如表2所示。 PH 酸碱度 出水端 表2 Housing数据特征选择及测试结果 Table 2 Feature selection and test results for Housing ORP, 氧化还原电位 mV 出水端 方法 特征选择结果 RMSE NH,-N 铵态氮浓度 mg/L 出水端 ALL x1-XB 4.350±0.515 NO-N 硝态氮浓度 mg/L 出水端 PLSR XaxsX6x 5.173±0.643 从北京市某污水处理厂获取了2015年6~8月共 MIFS(] xB,x1l,r4,x2 5.125±0.482 492组数据,首先剔除明显异常值,然后采用小波包 MRMR(0) (sym8小波2层分解、软阈值方式)进行降噪处理,处 XB6X10 3.880±0.476 理效果见图4。 CMIMI r13r6,r1r0 3.880±0.476 从原始数据集中每隔3个样本选取1个样本共 JMIt2) XBX6 4.187±0.598 123个组成测试集,其余369个作为训练集。TP数据 MM周 riB,t6,ri1,x 4.187±0.598 特征选择及MP网络测试结果如表4所示。相比 PLSR,kNN-FABC获得了较少的特征、较低的RMSE及 STEP[14] XBX6x8x1 4.187±0.488 其标准差,寻找到了最有效的特征子集,构建了更稳定 kNN-FABC XB,X6X5 3.710±0.406 的软测量模型,验证了kNN-FABC方法在特征选择上 注:ALL表示选取全部特征。 的有效性
作训练样本,1 000 个不含噪声数据作测试样本,变量 选择及网络测试结果如表 1 所示。 表 1 Friedman 数据特征选择及测试结果 Table 1 Feature selection and test results for Friedman 方法 变量选择结果 RMSE ALL x1 ~x12 3.101±1.274 PLSR x4,x2,x1,x5,x11,x12 3.543±1.440 MIFS [9] x4,x2,x1,x5,x6 2.002±0.095 MRMR [10] x4,x2,x1,x5,x6 2.002±0.095 CMIM [11] x4,x2,x1,x5,x6 2.002±0.095 JMI [12] x4,x2,x1,x5,x12 3.854±1.611 MMI [13] x4,x2,x1,x5,x12 3.854±1.611 STEP [14] x4,x2,x1,x5,x3 1.143±0.070 kNN⁃FABC x4,x2,x1,x5,x3 1.143±0.070 注: ALL 表示选取全部特征。 由表 1 可知, kNN⁃FABC 方法和文献[17]的 STEP 方法都成功筛选出全部仅有的 5 个相关特征,MRMR、 CMIM 和 MIFS 误剔相关特征 x3、误选无关特征 x6,JMI 和 MMI 误剔相关特征 x3、误选冗余特征 x12,PLSR 误 选冗余特征 x11和 x12。 同时,kNN⁃FABC 方法的 RMSE 均值和标准差都要远小于其他方法,表明其极大地提 高了网络泛化能力。 3.2 Housing 数据 Housing 数据由 13 个房屋属性的输入特征和 1 个 房屋价格的输出特征组成,共有 506 组样本。 随机选 择 338 组作训练样本,剩余 168 组作测试样本。 利用本 文方法进行特征选择,并与其他文献特征选择结果进 行了比较,特征选择及 MLP 网络测试结果如表2 所示。 表 2 Housing 数据特征选择及测试结果 Table 2 Feature selection and test results for Housing 方法 特征选择结果 RMSE ALL x1 ~x13 4.350±0.515 PLSR x4,x5,x6,x11 5.173±0.643 MIFS [9] x13,x11,x4,x2 5.125±0.482 MRMR [10] x13,x11,x6,x10 3.880±0.476 CMIM [11] x13,x6,x11,x10 3.880±0.476 JMI [12] x13,x6,x11,x7 4.187±0.598 MMI [13] x13,x6,x11,x7 4.187±0.598 STEP [14] x13,x6,x8,x1 4.187±0.488 kNN-FABC x13,x6,x5,x11 3.710±0.406 注:ALL 表示选取全部特征。 由表 2 可知,在归一化方法、MLP 模型参数选取一 致的情况下,kNN⁃FABC 的 RMSE 均值和标准差均表 明了采用本文方法所选特征建立的预测模型精度 更高。 3.3 污水处理出水总磷预测数据 近年来,总磷(total phosphorus, TP)污染问题开始 凸显。 研究表明,水体富营养化程度与总磷等指标密 切相关。 因此加强对 TP 的检测有助于解决水体富营 养化问题[20] 。 目前,污水处理厂普遍采用的生化方法 成本高、耗时长,在线检测仪表对检测环境要求高并且 维护成本昂贵,而基于数据驱动的软测量技术能够在 线、快速、准确预测,受到研究者青睐。 但是污水处理 生化反应过程中可测变量较多,在建立 TP 软测量模型 时,若选取全部可用特征,则会产生冗余,降低网络泛 化能力,同时也大幅增加检测成本,故对 TP 预测模型 进行输入特征选择具有重要意义。 污水处理生化反应 过程中可测变量及其意义如表 3 所示。 本文采用 kNN⁃FABC 方法实现对 TP 预测特征变量的选择。 表 3 可测变量的意义 Table 3 Significance of measurable variables 标记 参数 意义 单位 取样点 x1 T 水温 ℃ 厌氧池 x2 ORP1 氧化还原电位 mV 厌氧池 x3 DO1 溶解氧浓度 mg / L 好氧前端 x4 DO2 溶解氧浓度 mg / L 好氧末端 x5 TSS 总固体悬浮物浓度 g / L 好氧末端 x6 PH 酸碱度 - 出水端 x7 ORP2 氧化还原电位 mV 出水端 x8 NH4 -N 铵态氮浓度 mg / L 出水端 x9 NO3 -N 硝态氮浓度 mg / L 出水端 从北京市某污水处理厂获取了 2015 年 6~8 月共 492 组数据,首先剔除明显异常值,然后采用小波包 (sym8 小波、2 层分解、软阈值方式)进行降噪处理,处 理效果见图 4。 从原始数据集中每隔 3 个样本选取 1 个样本共 123 个组成测试集,其余 369 个作为训练集。 TP 数据 特征选择及 MLP 网络测试结果如表 4 所示。 相比 PLSR,kNN⁃FABC 获得了较少的特征、较低的 RMSE 及 其标准差,寻找到了最有效的特征子集,构建了更稳定 的软测量模型,验证了 kNN⁃FABC 方法在特征选择上 的有效性。 ·598· 智 能 系 统 学 报 第 12 卷

第5期 周红标,等:基于高维k-近邻互信息的特征选择方法 .599. 6 0.3 100 200 300400500 样本数/(个·样本1) (a)原始TP数据 4 40 6080100120 测试样本 图6TP数据MLP预测误差 100 200300400 500 Fig.6 Predicted error using MLP for TP 样本数/(个·样本1) (b)小波包去噪TP数据 4结束语 图4出水TP数据小波包去噪 通过将数据驱动型k-近邻方法扩展用于多维特征 Fig.4 Wavelet packet denoising for TP 之间相关性计算,结合前向累加策略,能够较为准确地 表4TP数据特征选择及测试结果 获得全部特征的最优排序,进而剔除无关特征,再结合 Table 4 Feature selection and test results for TP 后向交叉策略,能够定位并删除冗余特征,最终得到最 优强相关特征子集。Friedman、Housing和实际污水处 方法 特征选择结果 RMSE 理出水TP预测实验证实了本文方法的有效性。下一 步的研究工作是实现无关特征的自动判定,避免人为 ALL x-X9 0.428±0.077 设置带来的无关特征误剔的可能。 ERR X3,X4X8Xg 0.519±0.071 参考文献: PLSR x3x5.X2X1X6 0.464±0.033 [1]0SELEDETS I V,TYRTYSHNIKOV E E.Breaking the curse of dimensionality,or how to use SVD in many dimensions[J] kNN-FABC x7,1x26 0.159±0.004 SIAM journal on scientific computing,2009,31(5):3744-3759. [2]GHAMISI P,BENEDIKTSSON J A.Feature selection based 注:ERR为随机选取特征,作对比。 on hybridization of genetic algorithm and particle swarm 图5和图6分别给出了MP模型对TP数据预测 optimization[J].IEEE geoscience and remote sensing 结果和预测误差。可见,通过kNN-FABC方法选出的 1 etters,2015,12(2):309-313. [3]RAUBER T W,ASSIS BOLDT de F,VAREJAO F M. 特征能够很好地表征原始数据,建模误差主要集中在 Heterogeneous feature models and feature selection applied -0.3~0.3mg/L之间,能够较好地满足污水处理厂对总 to bearing fault diagnosis[J].IEEE transactions on 磷检测精度的要求。 industrial electronics,2015,62(1):637-646. [4]WOLD S,SJOSTROM M,ERIKSSON L.PLS-regression:a basic tool of chemometrics[J].Chemometrics and intelligent 一真实值 ----预测值 laboratory systems,2001.58(2):109-130. [5]SONG Q,SHEPPERD M.Predicting software project effort: a grey relational analysis based method[]].Expert systems 1-w) with applications,2011,38(6):7302-7316. [6]FENG J,JIAO L.LIU F,et al.Mutual-information-based semi-supervised hyperspectral band selection with high discrimination,high information,and low redundancy [J]. 0 20 40 60 80100120 IEEE transactions on geoscience and remote sensing,2015, 测试样本 53(5):2956-2969. 图5TP数据MP预测结果 [7]BENNASAR M,HICKS Y,SETCHI R.Feature selection Fig.5 Predicted output using MLP for TP using joint mutual information maximisation [J].Expert
(a)原始 TP 数据 (b)小波包去噪 TP 数据 图 4 出水 TP 数据小波包去噪 Fig.4 Wavelet packet denoising for TP 表 4 TP 数据特征选择及测试结果 Table 4 Feature selection and test results for TP 方法 特征选择结果 RMSE ALL x1 ~x9 0.428±0.077 ERR x3,x4,x8,x9 0.519±0.071 PLSR x3,x5,x2,x1,x6 0.464±0.033 kNN-FABC x7,x1,x2,x6 0.159±0.004 注: ERR 为随机选取特征,作对比。 图 5 和图 6 分别给出了 MLP 模型对 TP 数据预测 结果和预测误差。 可见,通过 kNN⁃FABC 方法选出的 特征能够很好地表征原始数据,建模误差主要集中在 -0.3~0.3 mg / L 之间,能够较好地满足污水处理厂对总 磷检测精度的要求。 图 5 TP 数据 MLP 预测结果 Fig.5 Predicted output using MLP for TP 图 6 TP 数据 MLP 预测误差 Fig.6 Predicted error using MLP for TP 4 结束语 通过将数据驱动型 k⁃近邻方法扩展用于多维特征 之间相关性计算,结合前向累加策略,能够较为准确地 获得全部特征的最优排序,进而剔除无关特征,再结合 后向交叉策略,能够定位并删除冗余特征,最终得到最 优强相关特征子集。 Friedman、Housing 和实际污水处 理出水 TP 预测实验证实了本文方法的有效性。 下一 步的研究工作是实现无关特征的自动判定,避免人为 设置带来的无关特征误剔的可能。 参考文献: [1]OSELEDETS I V, TYRTYSHNIKOV E E. Breaking the curse of dimensionality, or how to use SVD in many dimensions[J]. SIAM journal on scientific computing, 2009, 31(5): 3744-3759. [2]GHAMISI P, BENEDIKTSSON J A. Feature selection based on hybridization of genetic algorithm and particle swarm optimization [ J ]. IEEE geoscience and remote sensing letters, 2015, 12(2): 309-313. [3] RAUBER T W, ASSIS BOLDT de F, VAREJÃO F M. Heterogeneous feature models and feature selection applied to bearing fault diagnosis[J]. IEEE transactions on industrial electronics, 2015, 62(1): 637-646. [4]WOLD S, SJÖSTRÖM M, ERIKSSON L. PLS⁃regression: a basic tool of chemometrics[J]. Chemometrics and intelligent laboratory systems, 2001, 58(2): 109-130. [5]SONG Q, SHEPPERD M. Predicting software project effort: a grey relational analysis based method[ J]. Expert systems with applications, 2011, 38(6): 7302-7316. [6] FENG J, JIAO L, LIU F, et al. Mutual⁃information⁃based semi⁃supervised hyperspectral band selection with high discrimination, high information, and low redundancy [ J]. IEEE transactions on geoscience and remote sensing, 2015, 53(5): 2956-2969. [7] BENNASAR M, HICKS Y, SETCHI R. Feature selection using joint mutual information maximisation [ J ]. Expert 第 5 期 周红标,等:基于高维 k-近邻互信息的特征选择方法 ·599·

·600· 智能系统学报 第12卷 systems with applications,2015,42(22):8520-8532 [17]KRASKOV A,STOGBAUER H,GRASSBERGER P.Estimating [8]SHANNON C E.A mathematical theory of communication mutual information[J].Physical review E,2004,69(6): []ACM sigmobile mobile computing and communications 1-16 review,2001,5(1):3-55. [18]STOGBAUER H,KRASKOV A.ASTAKHOV S A,et al. [9]BATTITI R.Using mutual information for selecting features Least-pendent-component analysis based on mutual in supervised neural net learning[J].IEEE transactions on information[J].Physical review E,2004,70(6):1-17. neural networks,1994,5(4):537-550. [19]霍军周,王亚杰,欧阳湘宇,等.基于BP神经网络的 [10]PENG H,LONG F,DING C.Feature selection based on TBM主轴承载荷谱预测[J].哈尔滨工程大学学报, mutual information criteria of max-dependency,max-relevance, 2015,36(7):965-969. and min-redundancy[J.IEEE transactions on pattern analysis HUO Junzhou,WANG Yajie,OUYANG Xiangyu,et al.Load and machine intelligence,2005,27(8):1226-1238. spectrum prediction of the main drive bearing of a tunnel [11]FLEURET F.Fast binary feature selection with conditional boring machine based on BP neural networks[]].Joumal of mutual information[J].Journal of machine learning research, Harbin Engineering University,2015,36(7):965-969. 2004.5:1531-1555. [20]乔俊飞,周红标.基于自组织模糊神经网络的出水总磷 [12]YANG HH,MOODY J E.Data visualization and feature 预测[J].控制理论与应用.2017,34(2):224-232. selection:new algorithms for nongaussian data[C]/Advances QIAO Junfei,ZHOU Hongbiao.Prediction of effluent total in Neural Information Processing Systems.Cambridge, phosphorus based on self-organizing fuzzy neural network[] Britain,1999:687-693. Control theory and applications,2017,34(2):224-232. [13]BROWN G.A new perspective for information theoretic 作者简介: feature selection[C]//Proceedings of the 12th International 周红标,男,1980年生,讲师,博土 Conference on Artificial Intelligence and Statistics.Florida, 研究生,主要研究方向为神经网络分析 USA,2009:49-56. 与设计。发表论文十余篇,其中被 [14]韩敏,刘晓欣.基于互信息的分步式输入变量选择多元序 检索6篇。 列预测研究[J刀.自动化学报,2012,38(6):999-1005. HAN Min,LIU Xiaoxin.Stepwise input variable selection based on mutual information for multivariate forecasting [J].ACTA automatica sinica,2012,38(6):999-1005. 乔俊飞,男.1968年生,教授,博士 [15 BEIRLANT J,DUDEWICZ E J,GYORFI L,et al. 生导师,主要研究方向为污水处理过 Nonparametric entropy estimation:an overview[.Intemational 程智能优化控制。获教育部科技进步 journal of mathematical and statistical sciences,1997, 奖一等奖和北京市科学进步奖三等奖 6(1):17-39. 各1项,发表论文近100篇,其中被SC [16]MOON Y I.RAJAGOPALAN B.LALL U.Estimation of mutual information using kemel density estimators[J]. I收录18篇,EI收录60篇,获发明专利20项。 Physical review E,1995,52(3):2318-2321
生导师, 乔俊飞,男,1968 年生,教授,博士 主要研究方向为污水处理过 systems with applications, 2015, 42(22): 8520-8532. [8] SHANNON C E. A mathematical theory of communication [J]. ACM sigmobile mobile computing and communications review, 2001, 5(1): 3-55. [9]BATTITI R. Using mutual information for selecting features in supervised neural net learning[ J]. IEEE transactions on neural networks, 1994, 5(4): 537-550. [10]PENG H, LONG F, DING C. Feature selection based on mutual information criteria of max⁃dependency, max⁃relevance, and min⁃redundancy[J]. IEEE transactions on pattern analysis and machine intelligence, 2005, 27(8): 1226-1238. [11]FLEURET F. Fast binary feature selection with conditional mutual information[J]. Journal of machine learning research, 2004, 5: 1531-1555. [ 12] YANG H H, MOODY J E. Data visualization and feature selection: new algorithms for nongaussian data[C] / / Advances in Neural Information Processing Systems. Cambridge, Britain, 1999: 687-693. [13] BROWN G. A new perspective for information theoretic feature selection[C] / / Proceedings of the 12th International Conference on Artificial Intelligence and Statistics. Florida, USA, 2009: 49-56. [14]韩敏, 刘晓欣. 基于互信息的分步式输入变量选择多元序 列预测研究[J]. 自动化学报, 2012, 38(6): 999-1005. HAN Min, LIU Xiaoxin. Stepwise input variable selection based on mutual information for multivariate forecasting [J]. ACTA automatica sinica, 2012, 38(6): 999-1005. [ 15 ] BEIRLANT J, DUDEWICZ E J, GYÖRFI L, et al. Nonparametric entropy estimation: an overview[J]. International journal of mathematical and statistical sciences, 1997, 6(1): 17-39. [16] MOON Y I, RAJAGOPALAN B, LALL U. Estimation of mutual information using kernel density estimators [ J]. Physical review E, 1995, 52(3): 2318-2321. [17]KRASKOV A, STÖGBAUER H, GRASSBERGER P. Estimating mutual information[J]. Physical review E, 2004, 69(6): 1-16. [18]STÖGBAUER H, KRASKOV A, ASTAKHOV S A, et al. Least⁃pendent⁃component analysis based on mutual information[J]. Physical review E, 2004, 70(6): 1-17. [19]霍军周, 王亚杰, 欧阳湘宇, 等. 基于 BP 神经网络的 TBM 主轴承载荷谱预测[ J]. 哈尔滨工程大学学报, 2015, 36(7): 965-969. HUO Junzhou, WANG Yajie, OUYANG Xiangyu, et al.Load spectrum prediction of the main drive bearing of a tunnel boring machine based on BP neural networks[J]. Journal of Harbin Engineering University, 2015, 36(7): 965-969. [20]乔俊飞, 周红标. 基于自组织模糊神经网络的出水总磷 预测[J]. 控制理论与应用, 2017, 34(2): 224-232. QIAO Junfei, ZHOU Hongbiao. Prediction of effluent total phosphorus based on self⁃organizing fuzzy neural network[J]. Control theory and applications, 2017, 34(2): 224-232. 作者简介: 周红标,男,1980 年生,讲师,博士 研究生,主要研究方向为神经网络分析 与设计。 发表论文十余篇,其中被 EI 检索 6 篇。 程智能优化控制。 获教育部科技进步 600· 奖一等奖和北京市科学进步奖三等奖 I 收录 18 篇,EI 收录60 篇,获发明专利 20 项。 · 智 能 系 统 学 报 第 12 卷 各 1 项,发表论文近 100 篇,其中被 SC