同济大学：《空气动力学》课程电子教案（课件讲稿）Chapter 2 Some Fundamental Principles and Equations

Copyright by Dr.Zheyan Jin Chapter 2 Some Fundamental Principles and Equations Road Map Aerodynamics tools Review of vector relations Basic flow equations Useful concepts for the implementation of the basic flow equations Continuity equation Substantial derivative Momentum equation Streamline Vorticity Energy equation Circulation Stream function Velocity potential

Copyright by Dr. Zheyan Jin Road Map Aerodynamics tools Basic flow equations Review of vector relations Continuity equation Substantial derivative Momentum equation Energy equation Circulation Vorticity Streamline Chapter 2 Some Fundamental Principles and Equations Chapter 2 Some Fundamental Principles and Equations Useful concepts for the implementation of the basic flow equations Velocity potential Stream function

Copyright by Dr.Zheyan Jin Chapter 2 Some Fundamental Principles and Equations 2.1 Review of Vector Relations A vector V in the plane or in space is an arrow:it is determined by its length,denoted V and its direction. Some Vector Algebra A+B=C A-B=D A.B=A Blcose A×B=(ABsin0E=G B 6 B G Vector Vector Dot Cross Addition Subtraction Product Product

Copyright by Dr. Zheyan Jin A vector in the plane or in space is an arrow: it is determined by its length, denoted and its direction. Chapter 2 Some Fundamental Principles and Equations Chapter 2 Some Fundamental Principles and Equations 2.1 Review of Vector Relations Some Vector Algebra B  A  V AB  A Bcos   A  C  V  A B C      A  G B   B  B  A  D  A B D      Vector Addition Vector Subtraction A B A Bsin e G        θ Dot Product θ e  Cross Product

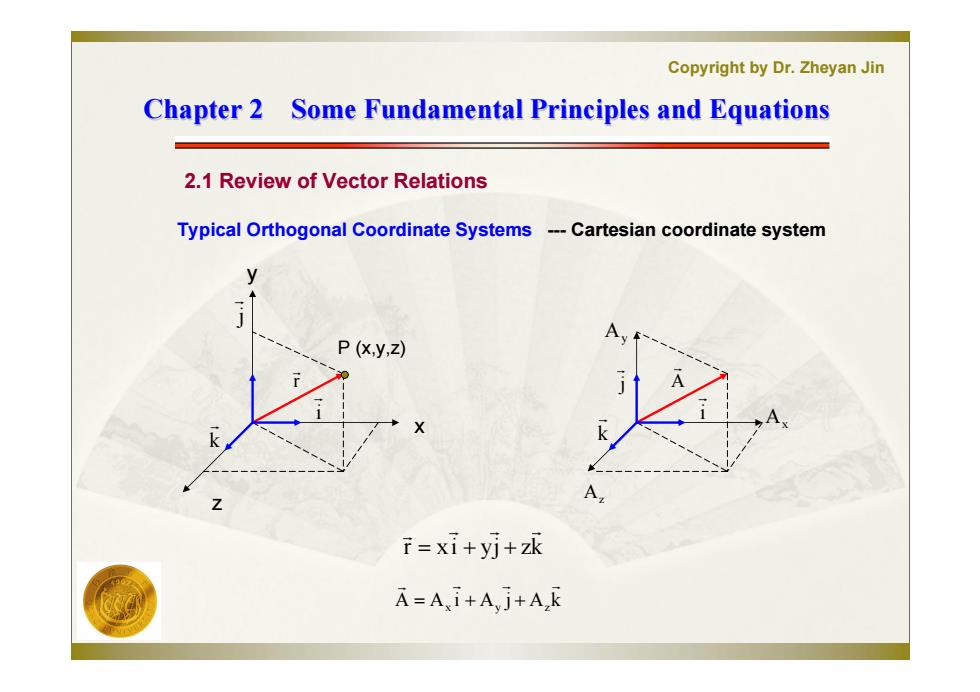
Copyright by Dr.Zheyan Jin Chapter 2 Some Fundamental Principles and Equations 2.1 Review of Vector Relations Typical Orthogonal Coordinate Systems ---Cartesian coordinate system y P (x,y,Z) f=xi+yj+z求 A=Ai+Ayj+Ak

Copyright by Dr. Zheyan Jin Chapter 2 Some Fundamental Principles and Equations Chapter 2 Some Fundamental Principles and Equations 2.1 Review of Vector Relations Typical Orthogonal Coordinate Systems j  Az Ax A A i A j A k x y z        i  r  k  r xi yj zk        --- Cartesian coordinate system P (x,y,z) y x z j  i  A  k  Ay

Copyright by Dr.Zheyan Jin Chapter 2 Some Fundamental Principles and Equations 2.1 Review of Vector Relations Typical Orthogonal Coordinate Systems ---Cylindrical coordinate system A X P(r ,z) x=rcos0 r=x+y A=A,e,+Age。+A,e2 y=rsine or 0=arctan Z=2 =2

Copyright by Dr. Zheyan Jin Chapter 2 Some Fundamental Principles and Equations Chapter 2 Some Fundamental Principles and Equations 2.1 Review of Vector Relations Typical Orthogonal Coordinate Systems Az r e  e A r r z z A A e A e A e          r  k  z z y r x r      sin cos --- Cylindrical coordinate system P(r,θ,z) y x z A  Ar θ z e z e r e  e z z x y r x y     arctan 2 2  or

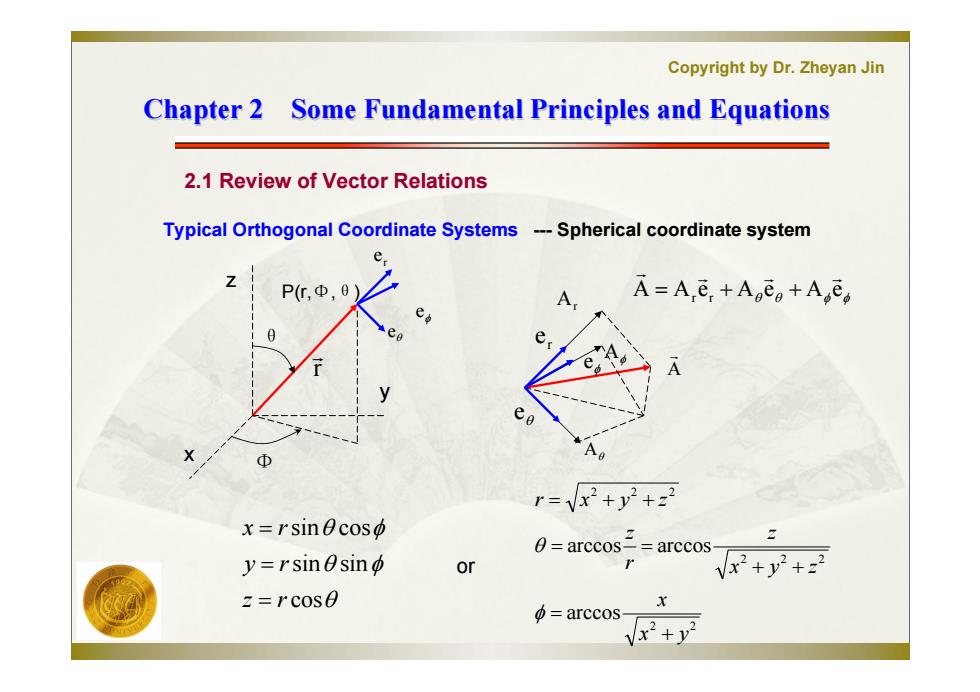
Copyright by Dr.Zheyan Jin Chapter 2 Some Fundamental Principles and Equations 2.1 Review of Vector Relations Typical Orthogonal Coordinate Systems ---Spherical coordinate system e Z P,，0 A=A,e+Aoeo+A e Φ r=Vx2+y2+22 x=rsinecoso 0-arccos==arccos- z y=rsinesin Or x2+y2+2 z=rcos0 X arccos- x2+2

Copyright by Dr. Zheyan Jin Chapter 2 Some Fundamental Principles and Equations Chapter 2 Some Fundamental Principles and Equations 2.1 Review of Vector Relations Typical Orthogonal Coordinate Systems r e  e     A A e A e A e r r        r       cos sin sin sin cos z r y r x r    --- Spherical coordinate system P(r,Φ,θ) z y x θ  e A Ar A  A  e r e  e 2 2 2 2 2 2 2 2 arccos arccos arccos x y x x y z z r z r x y z            or Φ

Copyright by Dr.Zheyan Jin Chapter 2 Some Fundamental Principles and Equations 2.1 Review of Vector Relations Scalar and Vector Fields: Scalar field:A scalar quantity given as a function of coordinate space and time t. p=p(x,y,z,)=P2(r,0,z,t)=P3(r,0,,) p=p1(x,y2,)=P2(r,0,z,t)=P3(c,0,,) T=T(x,y,2,t)=T(r,0,z,t)=T(,0,p,) Vector field:A vector quantity given as a function of coordinate space and time t. V=Vi+Vj+Vk V.=V.(x,y,zt) V,=V,(x.y,z.t) V.=V.(x,y,zt)

Copyright by Dr. Zheyan Jin Chapter 2 Some Fundamental Principles and Equations Chapter 2 Some Fundamental Principles and Equations 2.1 Review of Vector Relations Scalar and Vector Fields: V V (x, y,z,t) V V (x, y,z,t) V V (x, y,z,t) V V i V j V k z z y y x x x y z           ( , , , ) ( , , , ) ( , , , ) ( , , , ) ( , , , ) ( , , , ) ( , , , ) ( , , , ) ( , , , ) 1 2 3 1 2 3 1 2 3 T T x y z t T r z t T r t x y z t r z t r t p p x y z t p r z t p r t                       Scalar field: A scalar quantity given as a function of coordinate space and time t. Vector field: A vector quantity given as a function of coordinate space and time t

Copyright by Dr.Zheyan Jin Chapter 2 Some Fundamental Principles and Equations 2.1 Review of Vector Relations Scalar and Vector Products: A=Ai+Ayj+A k B=Bi+Byj+B,k A.B=A,Bs +A,By +A,B Cartesian Coordinates: AxB= Bx BB. A=Ae+Ao+A e B=B.e,+Boeo+Bez A.B=A,B,+AoBo+A,B, Cylindrical Coordinates: e,eo A×B= A:Ao A B,B。 B

Copyright by Dr. Zheyan Jin Chapter 2 Some Fundamental Principles and Equations Chapter 2 Some Fundamental Principles and Equations 2.1 Review of Vector Relations Scalar and Vector Products:               x y z x y z x x y y z z x y z x y z B B B A A A i j k A B A B A B A B A B A A i A j A k B B i B j B k               Cartesian Coordinates: Cylindrical Coordinates:               r z r z r z r r z z r z z r z z B B B A A A e e e A B A B A B A B A B A A e A e A e B B e B e B e                         r r

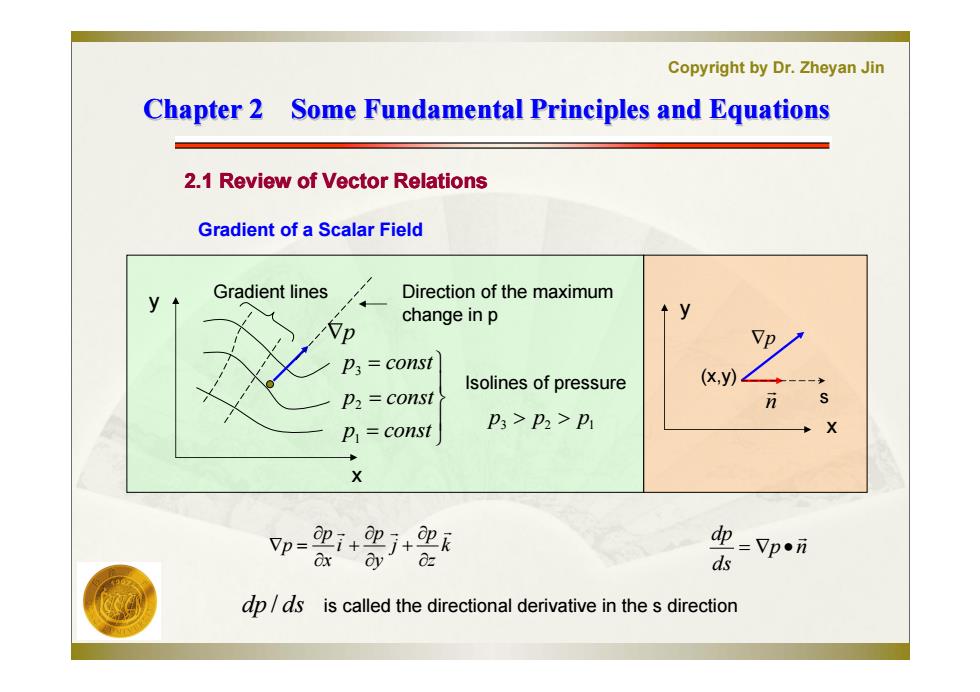
Copyright by Dr.Zheyan Jin Chapter 2 Some Fundamental Principles and Equations 2.1 Review of Vector Relations Gradient of a Scalar Field Gradient lines Direction of the maximum p change in p ↑y p3 =const Isolines of pressure (xy） P2=const p=const P3>P2>P X X p=2i+2j+史x =Vpn ds p/ds is called the directional derivative in thes direction

Copyright by Dr. Zheyan Jin Chapter 2 Some Fundamental Principles and Equations Chapter 2 Some Fundamental Principles and Equations 2.1 Review of Vector Relations Gradient of a Scalar Field p k z p j y p i x p p           p n ds dp     n  Gradient lines p      p const p const p const 1 2 3 Isolines of pressure 3 2 1 p  p  p Direction of the maximum change in p x y (x,y) s x y dp / ds is called the directional derivative in the s direction 2.1 Review of Vector Relations Chapter 2 Some Fundamental Principles and Equations Chapter 2 Some Fundamental Principles and Equations

Copyright by Dr.Zheyan Jin Chapter 2 Some Fundamental Principles and Equations 2.1 Review of Vector Relations Example 1: fΦ=1/r,findV f=xi+y+z求 V= i+0j+2 a x2+y2+z29 Vx2+y2+z2)3 Vx2+y2+z2)9 7中= xi+yi+z求 Vx2+y2+z2)

Copyright by Dr. Zheyan Jin Chapter 2 Some Fundamental Principles and Equations Chapter 2 Some Fundamental Principles and Equations 2.1 Review of Vector Relations Example 1: If Φ=1/r, find  k ˆ j z ˆ i y ˆ r  x    3 2 2 2 3 2 2 2 3 2 2 2 3 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 r r x y z ˆ x ˆ y ˆ z x y z ˆ z x y z y ˆ x y z x ˆ ˆ x y z 1 ˆ x y z 1 ˆ x y z 1 x y z 1 r 1                                                              （ ） （ ） （ ） （ ） i j k i j k k z j y i x k z j y i x             

Copyright by Dr.Zheyan Jin Chapter 2 Some Fundamental Principles and Equations 2.1 Review of Vector Relations Example 2:Find directional derivative of=x+4x2 at point(1,-2,1) in the direction of 2-j-2 =x2yz+4xz2 Vo=(2xyz+422,x2=,x2y+8xz) =Vpi d At point(1,-2,1)Vp=(0,l,6) The unit vector for 2-j-2k Directional derivative is

Copyright by Dr. Zheyan Jin Chapter 2 Some Fundamental Principles and Equations Chapter 2 Some Fundamental Principles and Equations 2.1 Review of Vector Relations  （0，1，6） k ˆ j 2 ˆ i ˆ 2   Example 2: 3 1 4 3 2 3 1 3 2 （0，1，6）（ ， ， ）  in the direction of （ ， ， ） 3 2 3 1 3 2   2xyz 4 8 ) 4xz 2 2 2 2 2 z x z x y xz x yz        （ ， ，  Find directional derivative of 2 2   x yz  4xz k ˆ j 2 ˆ i ˆ 2   at point (1,-2,1) The unit vector for At point (1,-2,1) p n ds dp     Directional derivative is is