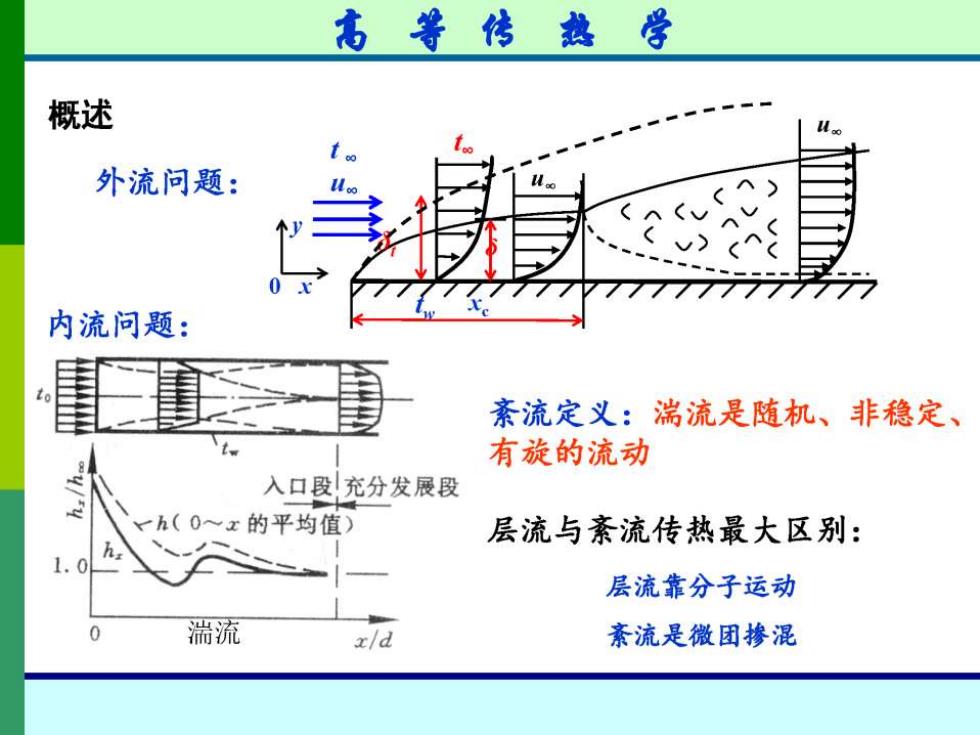
高等传热学 概述 外流问题: 内流问题: 紊流定义:湍流是随机、非稳定、 有旋的流动 入口段充分发展段 ~h(0~x的平均值) 层流与紊流传热最大区别: 1.0 层流靠分子运动 湍流 x/d 紊流是微团掺混

高等传热学 §1紊流边界层的连续方程与动量方程 (方程) 一、时均速度与脉动速度 时间平均速度:可= T+△T △ Vidt AAA 瞬时物理量:V:=可+Vt 速度 p=币+p' 脉动 压力 t=i+t t' 温度 根据定义 t+△T 1 T+△T △元 (可+V)dπ = Vi'dr =0 同理: p'=t=0 常用规则: 但: VV+0 平均导数 导数平均
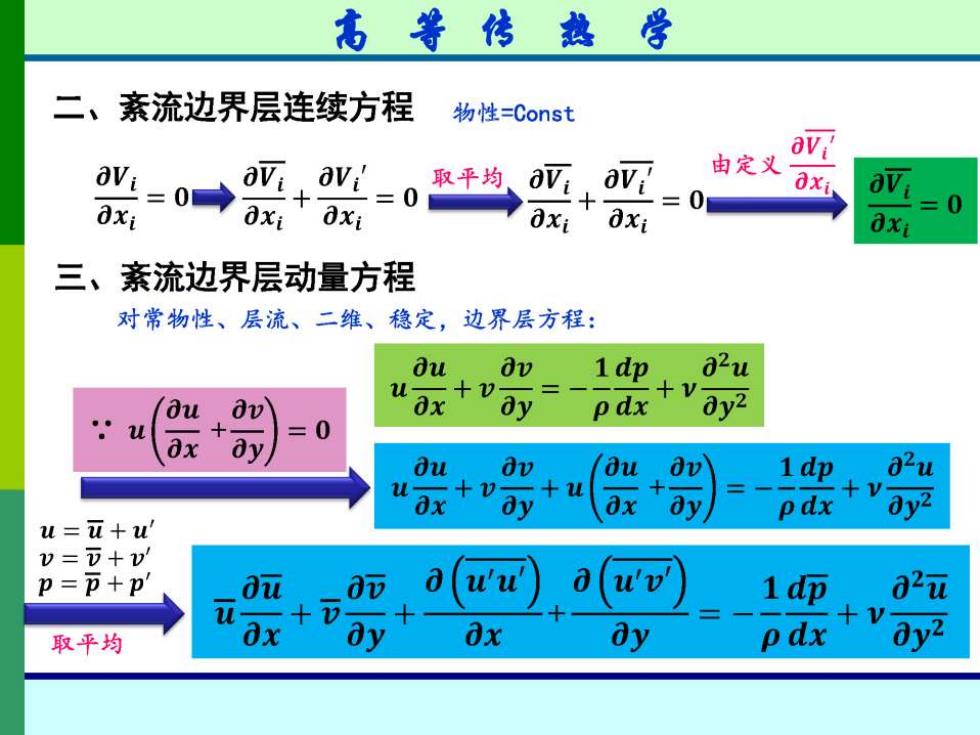
高等传热学 二、紊流边界层连续方程 物性=Const av aVi=0→ avi avi' 取平均 可,a 由定义 0xi =0 =0 0xi 0xi =0 0x 三、紊流边界层动量方程 对常物性、层流、二维、稳定,边界层方程: o dv 1dp 82u u -+0 +V- 0 ay pdx y2 0 dy ou dv av 1dp 82u +u + 0x ay pdx 0y2 u=u+u' V=)+v' P=p+p 0元 1dp 02元 u +v 取平均 p dx 0y2
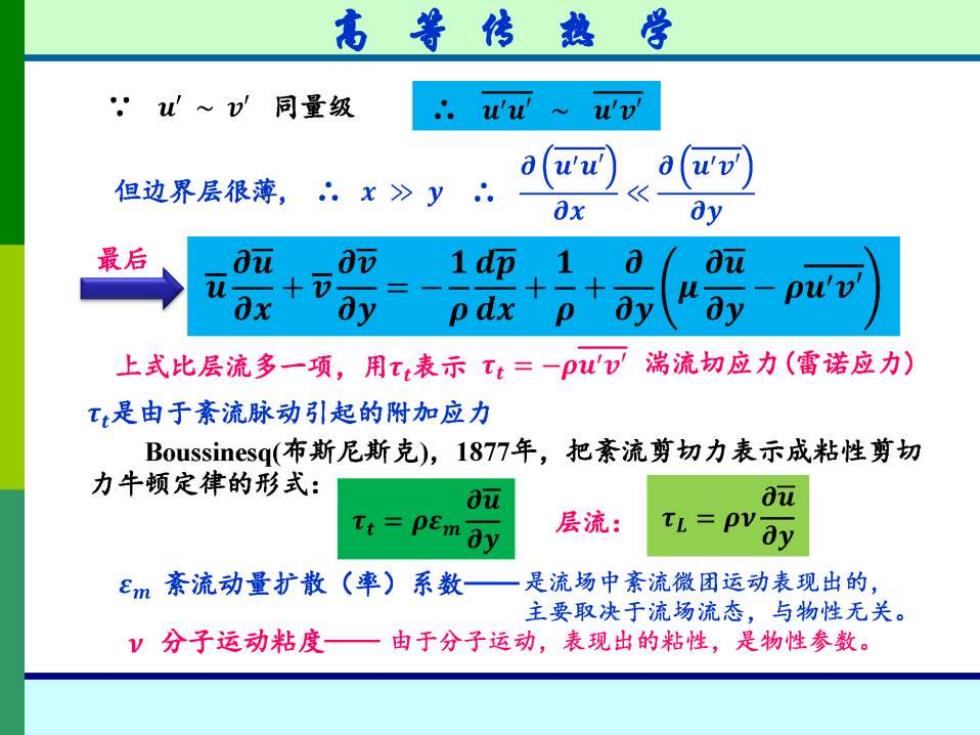
高等传热学 ”u'v 同量级 u'u ~uv (uu ∂(u'v 但边界层很薄,。x》 y 最后 ou 0而 1dp 1 pu'v 0x dy pdx p 上式比层流多一项,用tt表示:=一pu'v 湍流切应力(雷诺应力)》 T:是由于紊流脉动引起的附加应力 Boussinesq(布斯尼斯克),1877年,把紊流剪切力表示成粘性剪切 力牛顿定律的形式: Ou ∂u Tt=pEm 层流: TL=PV dy ay em素流动量扩散(率)系数 一是流场中紊流微团运动表现出的, 主要取决于流场流态,与物性无关。 V分子运动粘度一 由于分子运动,表现出的粘性,是物性参数
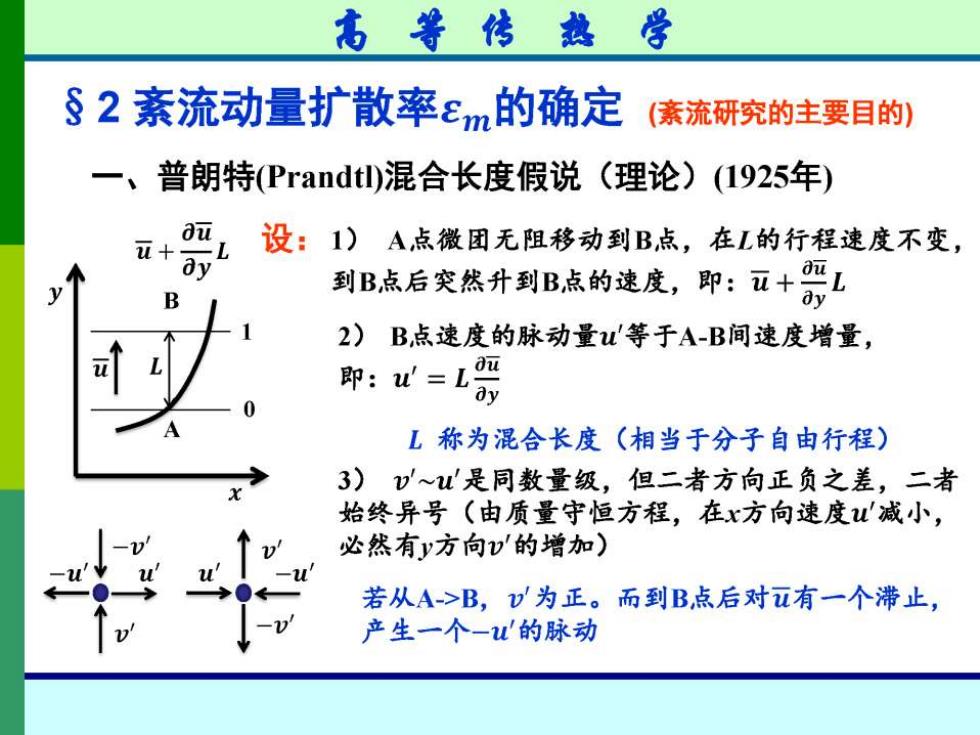
高等传热学 §2紊流动量扩散率εm的确定 (紊流研究的主要目的) 一、普朗特Prandt)混合长度假说(理论)(1925年) 设:1)A点微团无阻移动到B,点,在L的行程速度不变, ay B 到B点后突然升到B点的速度,即:五+L 2)B,点速度的脉动量等于A-B间速度增量, 聊:让= L称为混合长度(相当于分子自由行程) 2 3)v~是同数量级,但二者方向正负之差,二者 始终异号(由质量守恒方程,在x方向速度减小, 必然有y方向v的增加) 若从A->B,v为正。而到B点后对ū有一个滞止, 产生一个-'的脉动

高等传热学 ∴.lv1=L dy =u' -u= ( t=-pu=pL2 ay ay Em =L2 dy 由于紊流流动时绕流壁面的结果,在壁面附近必然是会有显著的变 化。实验证明了这一点,在边界层内速度向壁而减小,在壁面为0,则紊 流动量扩散率也应=0。 因此假设混合长度正比距离壁面的距离,即:L=ky 实验得:在近壁,k=0.4,y/6≤0.2 在紊流核心外侧部分,L=0.0856,y/6>0.2 尽管这个模型很简单,对许多边界层问题得到的结果令人满意

高等传热学 §3光滑管内的通用速度型 (求解速度场) 在湍流运动中,存在粘性应力和紊流应力的总和作用 du du 小总应力t=tL+=y+p2 是管内充分发展段 dy 偏微分方程改为常微分方程 另外,为了方便,把元改为 uc管轴线 1.粘性底层(层流应力>>紊流应力) R 紊流核心 此层T》tt或(y》em),主要靠分 ub 子分子运动传递动力(层流) 粘性底层 ,粘性底层很薄 ∴,速度分布认为是线性变化的 du .t=t红=Tw= =vp dy 0

高等传热学 令 w是速度因次,Prandtl称之为切应力速度 (剪切速度),用u,表示,但不是真实速度 令: ut ut ur 无量纲通用速度 y+= 无量纲距离 .u*=y时 粘性底层通用速度型 底层边界的速度为: ub+= up δbur ur 对粘性底层交界处: R Rut sm=92九E物 vub+ 6b= vub
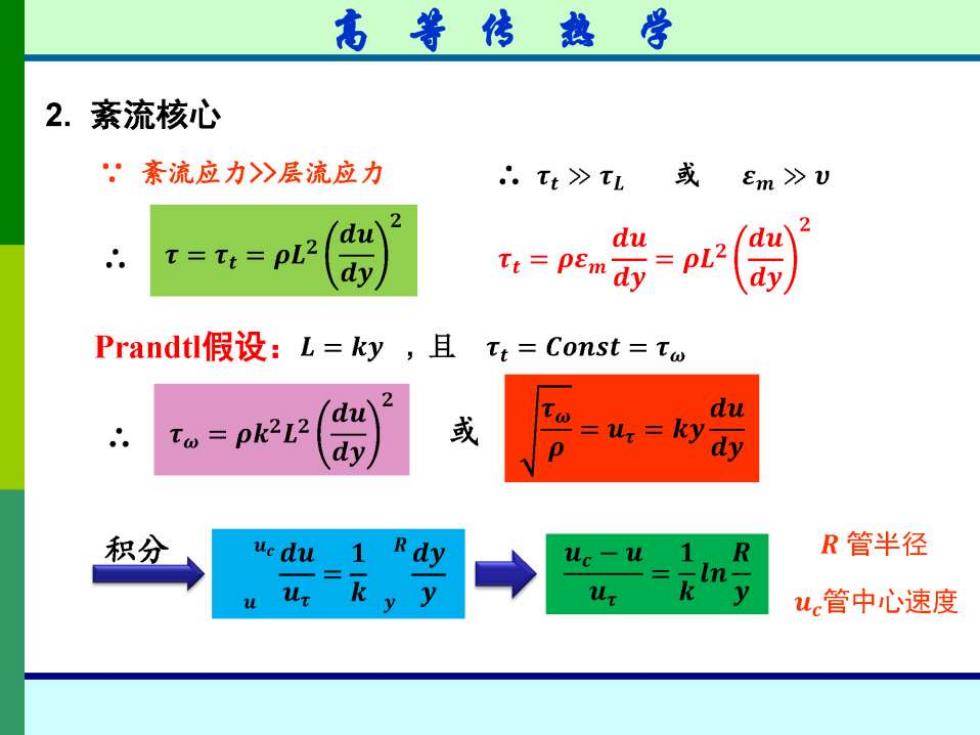
高等传热学 2.紊流核心 ,紊流应力>》层流应力 ∴.Tt>TL 或 Em >>U 2 du T Tt=pL2 du dy tt=pEm dy pL2 dy Prandtl假设:L=ky,且 Tt=Const=To 2 du du To pk212 或 dy ur=ky dy 积分 uc du 1 dy uc-u R管半径 ln ur k y ur k y u管中心速度

高等传热学 ,尼古拉兹实验得:k=0.4 uc u R =2.5lm u 写成通用速度: R ut =uc+-2.5ln 对粘性底层交界处: R up+uc+-2.5In- vup =we+-2.5lm Rut ×66= ur vub+