
第州黄月 Vol DX0l,10.3785/.issm.1008-973X.2014.03.014 直角绝热边界附近少量冻结管稳态温度场解析解 胡向东,郭旺,张洛瑜 (同济大学地下建筑与工程系,岩士及地下工程教育都重点实验室,上海20092 要:针对地层在进行人工冻结时,由于冻士雏受到既有地下构筑物的限制而无法自由发展的实际情况,研究 直角构筑物附近少量冻结管温度场这一工程问题,将该工程问题抽象成1/4平面内直角绝热边界附近布置少量 冷源稳态温度 }函数叠加法结合镜像法的求解方法.采用镜像法将1/平面问题映射成无限区域 ,应用势函数叠 法进行求解.通过理论排导,求 了直角绝热边界附近单管和双 冻 的是 温度场解析角 采用热学数值模椒方法对冻结管布置不同时的解析解分别进行验证,结果表明,解析解计算温度场与数值模拟 果吻合 关键词:人工地层冻结法:地热边界:冻结管:稳态温度场:解析解:势函数 中图分类号:TU472. 文章编号:1008-973X(2014)03-0471-07 Analytical solution of steady state temperature field of a few freezing pipes arranged near a right angle adiabatic boundary HU Xiang-dong.GUO Wang,ZHANG Luoyu (Department of Geotechnical Engineering.Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education.Tongji University.Shanghai 200092.China) Abstract.Aiming at the actual situation that the development of frozen soil often subiects to existing un derground structures in artificial ground freezing projects,the engineering problem of the temperature field of a few freezing pipes anged near right angle struetures was studied.The study subjeets were abstrac ed into quarterplane problems of a few point cold sources arranged near a rightangle adiabatic boundary. A solution method combining the potential superposition method with the mirror image method was pro posed.With the quarter-plane problems mapped into infinite region problems by the mirror image method, the potential superposition method was then employed for the solution.After theoretical derivations,the steady-state temper ature fields of single-piped and double-piped freezing near a right-angle adiabatic bound- ary were obtained analytically.All the analytical formu for different f ezing pipes were verified by thermal numerical simulation,and the results showed that the temperature fields calculated by the analytical formulas were well consistent with those by thermal numerical simulation for the same conditions. Key words:artificial ground freezing:adiabatic boundary:freezing pipes:steady state:temperature filed potential function 冻结法的工作原理是利用人工制冷技术,使地 较好的封水效果和力学强度,以及冻结法在保护周 层中的水结冰,形成能第抵抗外界水土压力的冻土 边环境和安全方面的优越性,该方法被广泛应用于 推幕,并将其作为临时支撞结构。由于冻土推幕具有 盾构进出洞、基坑支护、山竖井等工程建设中.在 收稿日期:20121226 浙江大学学报(工学版)网址: urnals.ziu.edu.en/eng 基金项目:国家自然科学基全资助项日(61178336):浙江省自然科学基金资助项日(1Z13E080002). 作者简介:明向东(961一),男,刷教授,博导,主要从事隧道与地下工程方面的教学与所究工作, 1994-015 China Academic Joumal Electronic Publishing House.All rights reserved.htp://www.enki.net
第48卷第3期 2014年3月 浙 江 大 学 学 报 (工学版) JournalofZhejiangUniversity(EngineeringScience) Vol.48No.3 Mar.2014 收稿日期:2012-12-26. 浙江大学学报(工学版)网址:www.journals.zju.edu.cn/eng 基金项目:国家自然科学基金资助项目(51178336);浙江省自然科学基金资助项目(LZ13E080002). 作者简介:胡向东(1961-),男,副教授,博导,主要从事隧道与地下工程方面的教学与研究工作. E-mail:anton.geotech@tongji.edu.cn DOI:10.3785/j.issn.1008-973X.2014.03.014 直角绝热边界附近少量冻结管稳态温度场解析解 胡向东,郭 旺,张洛瑜 (同济大学 地下建筑与工程系,岩土及地下工程教育部重点实验室,上海 200092) 摘 要:针对地层在进行人工冻结时,由于冻土帷幕受到既有地下构筑物的限制而无法自由发展的实际情况,研究 直角构筑物附近少量冻结管温度场这一工程问题.将该工程问题抽象成1/4平面内直角绝热边界附近布置少量点 冷源稳态温度场问题,提出势函数叠加法结合镜像法的求解方法.采 用 镜 像 法 将1/4平面问题映射成无限区域问 题,应用势函数叠加法进行求解.通过理论推导,求得了直角绝热边界附近单管和双管冻结的稳态温度场解析解. 采用热学数值模拟方法对冻结管布置不同时的解析解分别进行验证,结 果 表 明,解析解计算温度场与数值模拟结 果吻合. 关键词:人工地层冻结法;绝热边界;冻结管;稳态温度场;解析解;势函数 中图分类号:TU472.9 文献标志码:A 文章编号:1008-973X(2014)03-0471-07 Analyticalsolutionofsteadystatetemperaturefieldof afewfreezingpipesarrangedneararightangleadiabaticboundary HU Xiang-dong,GUO Wang,ZHANGLuo-yu (DepartmentofGeotechnicalEngineering,KeyLaboratoryofGeotechnicalandUnderground EngineeringofMinistryofEducation,TongjiUniversity,Shanghai200092,China) Abstract:Aimingattheactualsituationthatthedevelopmentoffrozensoiloftensubjectstoexistingun- dergroundstructuresinartificialgroundfreezingprojects,theengineeringproblemofthetemperaturefield ofafewfreezingpipesarrangednearrightanglestructureswasstudied.Thestudysubjectswereabstract- edintoquarter-planeproblemsofafewpointcoldsourcesarrangedneararight-angleadiabaticboundary. Asolutionmethodcombiningthepotentialsuperpositionmethodwiththemirrorimagemethodwaspro- posed.Withthequarter-planeproblemsmappedintoinfiniteregionproblemsbythemirrorimagemethod, thepotentialsuperpositionmethodwasthenemployedforthesolution.Aftertheoreticalderivations,the steady-statetemperaturefieldsofsingle-pipedanddouble-pipedfreezingneararight-angleadiabaticbound- arywereobtainedanalytically.Alltheanalyticalformulasfordifferentarrangementsoffreezingpipeswere verifiedbythermalnumericalsimulation,andtheresultsshowedthatthetemperaturefieldscalculatedby theanalyticalformulaswerewellconsistentwiththosebythermalnumericalsimulationforthesameconditions. Keywords:artificialgroundfreezing;adiabaticboundary;freezingpipes;steadystate;temperaturefiled; analyticalsolution;potentialfunction 冻结法的工作原理是利用人工制冷技术,使地 层中的水结冰,形成能够抵抗外界水土压力的冻土 帷幕,并将其作为临时支撑结构.由于冻土帷幕具有 较好的封水效果和力学强度,以及冻结法在保护周 边环境和安全方面的优越性,该方法被广泛应用于 盾构进出洞、基坑支护、矿山竖井等工程建设中.在

472 浙江大学学报(工学) 第48 冻结工程中,冻土的力学性质,冻土帷幕的厚度等耳 根据傅里叶定律和热力学第一定律,平面内热 要参数都依赖于冻结温度场的分布,因此,冻结温度 传导的控制方程为 场的计算是人工冻结法理论研究的基础. 人工冻土温度场的计算方法主要有解析法、模把 +-Q+-0 (3) 法以及数值分析法三类,解析法由于其在理论上的可 式中:g,、4,分别代表单位时间内沿x、y方向的热 性,始终是研穷的一个重要部分此外,老虑到人 流量,Q代表单位时间、单位体积系统从外界吸收或 地层冻结后期发展缓慢 其温度场非常接近稳态导热 向外界放出的热量为士体密度,为士体比热容 温度场,对此状态可按稳态导热求解人工冻结温度 在推导过程中将士体假设为各向同性材料,即 场,这一观点被学术界和工程界普遍接受和 沿各方向传热系数均相等,在计算区内不考虑系统 基于稳态导热理论,各国专家、学者们已经取得 与外界的热量交换,将热势定义和稳态条件代入控 了很多稳态温度场解析解:Trupak[叮和Bakho 制方程,式(3)可进一步化简为 ]分别提出了单管、单排和双排族结特的族士堆 幕温度场计算方法] +-0 (4) :等)也研究获得了单挂 管温度场分布公 线形冻土帷落的温度场.在国内,陈文豹等 式(4)的极坐标形式为 ()=0 人工冻结温度场进行了研究,笔者也对稳态温度场 的计算公式讲行了研究和完善1可.姚而,这些公式 由上述讨论可知,Laplace方程的解即为热势函 都是基于冻土帷幕自由发展的情况,没有考虑冻结 数.以单管情形为基础,将各管产生热势的原理看作 管周边可能存在的边界限制 是各管圆心,处存在一冷酒,在稳态时该点冷源单侣 在实际工程中,在布置的冻结管附近常常存在 时间的吸热量为q。,则其存在会使平面内每点都会 如地铁,地下街道,地下市政设施以及地下室等地下 产生 一定的温度势降低根据势 叠加原理,在平 构筑物,这些构筑物会对土体热量的传导产生影响 面内存在多个这样的点冷源时,这种热势的降低是 从而影响温度场的分布,在这样的情况下,采用无边 可以叠加的,因此,当平面内布置多根冻结管时,平 界限制的温度场计算公式就会产生较大误差.直角 面内任一点的热势等于各管中心冷源在该点产生的 绝热边界即为:利用冻结法对基坑阳角进行封水, 热势的叠加 结孔附近的地连墙表面 一般会铺上隔热板来抑制 根据以上假设,在点冷源周围画上从点冷源到任 量散发以保持冻结效果,因此,地连墙可以近似地看 意点距离r为半径的圆,圆周上一点的热流量为4,则 成是绝热边界,此种情况就可以看作是在冻结管 近存在一直角绝热边界本文基于稳态导热理论,采 =2=-2ar 用镜像法和 函数叠加法推导了直角绝热边界附近 并由此得到: 布置少量冻结管时的稳态温度场解析解。 腰=-中=-nr+C. (5) 1热势定义及势函数叠加原理 当平面上存在根冻结管时,即n个点冷源时,冻结 区内任意一点的势为 在土体中,热传递主要有3种形式:传导、对流 =-(nn+1n+…+nrC.(6) 辐射.在一般的工程应用中,后两者对推导结果的 响相对于前者可以忽略不计,因此,本文的推导中不 即 考虑后2种热传递形式。 =-n+C 根据傅里叶定律: 式中:”为该点到第i根冻结管中心的距离,g为第 (1) :根冻结管的热流量,C为积分常数」 式中:9,代表沿单位时间内x方向的热流量,k代表 土体的传热系数,0代表土体温度.令D一0,将其定 无限大区域内单根冻结管的稳态 义为热势,则有 温度场求解 ,=-骋 (2) 本文中采用定义热势函数的方法来求解无限大 194-2015 China Academic Joumal Electronic Publishing House. .All rights re erved. http://www.cnki.ne
冻结工程中,冻土的力学性质、冻土帷幕的厚度等重 要参数都依赖于冻结温度场的分布,因此,冻结温度 场的计算是人工冻结法理论研究的基础. 人工冻土温度场的计算方法主要有解析法、模拟 法以及数值分析法三类,解析法由于其在理论上的可 靠性,始终是研究的一个重要部分.此外,考虑到人工 地层冻结后期发展缓慢,其温度场非常接近稳态导热 温度场,对此状态可按稳态导热求解人工冻结温度 场,这一观点被学术界和工程界普遍接受[1-4] . 基于稳态导热理论,各国专家、学者们已经取得 了很 多 稳 态 温 度 场 解 析 解:Trupak[1]和 Bakhol- din[2]分别提出了单管、单排和双排冻结管的冻土帷 幕温度场计算方法;Sanger等[3]也研究获得了单排 管温度场分布 公 式;户 部 畅 等[4-5]得出了多管等间 距直线形冻土帷幕的温度场.在国内,陈文豹等[6]对 人工冻结温度场进行了研究,笔者也对稳态温度场 的计算公式进行了研究和完善[7-15] .然而,这些公式 都是基于冻土帷幕自由发展的情况,没有考虑冻结 管周边可能存在的边界限制. 在实际工程中,在布置的冻结管附近常常存在 如地铁、地下街道、地下市政设施以及地下室等地下 构筑物,这些构筑物会对土体热量的传导产生影响, 从而影响温度场的分布.在这样的情况下,采用无边 界限制的温度场计算公式就会产生较大误差.直角 绝热边界即为:利用冻结法对基坑阳角进行封水,冻 结孔附近的地连墙表面一般会铺上隔热板来抑制热 量散发以保持冻结效果,因此,地连墙可以近似地看 成是绝热边界,此种情况就可以看作是在冻结管附 近存在一直角绝热边界.本文基于稳态导热理论,采 用镜像法和势函数叠加法推导了直角绝热边界附近 布置少量冻结管时的稳态温度场解析解. 1 热势定义及势函数叠加原理 在土体中,热传递主要有3种形式:传导、对流、 辐射.在一般的工程应用中,后两者对推导结果的影 响相对于前者可以忽略不计,因此,本文的推导中不 考虑后2种热传递形式. 根据傅里叶定律: qx =-kθ x. (1) 式中:qx 代表沿单位时间内x 方向的热流量,k代表 土体的传热系数,θ代表土体温度.令Φ=kθ,将其定 义为热势,则有 qx =-Φ x. (2) 根据傅里叶定律和热力学第一定律,平面内热 传导的控制方程为 qx x+qy y-Q+ρcθ t=0. (3) 式中:qx、qy 分别 代 表 单 位 时 间 内 沿x、y 方 向 的 热 流量,Q 代表单位时间、单位体积系统从外界吸收或 向外界放出的热量,ρ为土体密度,c为土体比热容. 在推导过程中将土体假设为各向同性材料,即 沿各方向传热系数均相等.在计算区内不考虑系统 与外界的热量交换,将热势定义和稳态条件代入控 制方程,式(3)可进一步化简为 2 Φ x2 +2 Φ y2 =0. (4) 式(4)的极坐标形式为 d drrdΦ ( ) dr =0. 由上述讨论可知,Laplace方程的解即为热势函 数.以单管情形为基础,将各管产生热势的原理看作 是各管圆心处存在一冷源,在稳态时该点冷源单位 时间的吸热量为qc,则其存在会使平面内每点都会 产生一定的温度势降低.根据势函数叠加原理,在平 面内存在多个这样的点冷源时,这种热势的降低是 可以叠加的,因此,当平面内布置多根冻结管时,平 面内任一点的热势等于各管中心冷源在该点产生的 热势的叠加. 根据以上假设,在点冷源周围画上从点冷源到任 意点距离r为半径的圆,圆周上一点的热流量为qc,则 qc =2πrq =-2πrdΦ dr, 并由此得到: dΦ dr=- qc 2πr,Φ =-qc 2π lnr+C . (5) 当平面上存在n根冻结管时,即n个点冷源时,冻结 区内任意一点的势为 Φ =- qc1 2π lnr1 +qc2 2π lnr2 + … +qcn 2π ( ) lnrn +C .(6) 即 Φ =- ∑ n i=1 qci 2π lnri +C . 式中:ri 为该点到第i根冻结管中心的距离,qci为第 i根冻结管的热流量,C 为积分常数. 2 无限大区域内单根冻结管的稳态 温度场求解 本文中采用定义热势函数的方法来求解无限大 274 浙 江 大 学 学 报 (工学版) 第48卷

第3期 胡向东,等:直角绝热边界附近少量冻结管稳态温度场解析解 473 区域内单根冻结管稳态温度场的情况。由于冻结管 吸收热量,将其看作是点冷源,并使其处于坐标中 冻土边界 心,冻结管示意图见图1,图中:冻结管半径为。,冻 绝热面 土半径为:,冻结管表面温度为,土体冻结温度为 风,冻结管热流量为g 基坑内 、冻土边界 基坑阳角处 (a)当和大小按近时 结管 冻土边界 绝热面 冻管 基坑内部 1g. 冻结区域内任意点M(x,y)的热势函数的表 基坑阳角处 达式与式(5)相同,r的表达式为 内 热面 -y ()当较大较小时 冻土边界一点的势为 y1 -+C; 冻土边界 绝热面 冻结管边缘一点的势为 m-号Inn+C (8) 基坑内部 联立式(7)与式(8)可以解得: -是影=n(1月 基坑阳角处 基坑内 绝热面 将得出的4.表达式代入式(5),并记M点的热势 (c)当d较小/较人时 中,、温度Q.,再利用关系式:,-,-。和 图?直角绝热边界处单根冻结管示意图 ,最终得出无限大区域内单根冻结管稳态温度场 Fig.2 ering pipe ngle a的解为 -a+a-4 (9) 态温度场比较闲难,为此,酒过错像法,以2个技 其中日和品分别为冻结管边缘和冻土边界的温度. 面为镜面分别找到单管的2个镜像,再找出 个平 式(9)与特鲁巴克单管温度场的解)是完全相同的。 衡像(这是为了使直角绝热面两直角边保特其绝 性质),最终将单管族结映射成以绝热边界为对称轴 3 直角绝热边界附近布置单根冻结管 的四管句题,然后通过势函数叠加法来求解,见图 的情形 3由对称性可知,在映射后四管的对称轴处,即原绝 热边界 工,y方向始终没有热流量 ,因此,达到稳 3.1温度场解析解 态后,映射在上半平面第一象限内的单管温度场分 在直角绝热边界附近布置单根冻结管,该冻结 布与原问题等效. 管距热边界的距离分别为d和1,冻结管中心沿y 图3中冻结管与3根镜像管中心的坐标分别为 方向到冻土边界的距离为1,见图2. P(,d0.J1(-,d0,J2(-l, 在冻结管表面温度一定的情况下要直接求解稳 定义冻士边界条件点,其与冻结管中心P的连线与 994-2015 China Academie Joumal Electronic Publishing House.All rights reserved.http://www.enki.ne
区域内单根冻结管稳态温度场的情况.由于冻结管 吸收热量,将 其 看 作 是 点 冷 源,并使其处于坐标中 心,冻结管示意图见图1,图中:冻结管半径为r0,冻 土半径为ξ,冻结管表面温度为θf,土体冻结温度为 θ0,冻结管热流量为qc. 图1 无限大区域内单根冻结管示意图 Fig.1 Onefreezingpipeininfiniteregion 冻结区域内 任 意 点 M(x,y)的热势函数的表 达式与式(5)相同,r的表达式为 r= x2 槡 +y2 . 冻土边界一点的势为 Φ0 =-qc 2π lnξ+C ; (7) 冻结管边缘一点的势为 Φf =-qc 2π lnr0 +C . (8) 联立式(7)与式(8)可以解得: -qc 2π= Φf-Φ0 ln(r0/ξ), 将得出的qc 表 达 式 代 入 式(5),并 记 M 点 的 热 势 Φs、温度θs,再利用关系式:Φs=kθs、Φ0=kθ0 和Φf= kθf,最终得出无限大区域内单根冻结管稳态温度场 θs 的解为 θs =θ0 +ln(r/ξ) ln(r0/ξ) (θf-θ0). (9) 其中θf 和θ0 分别为冻结管边缘和冻土边界的温度. 式(9)与特鲁巴克单管温度场的解[1]是完全相同的. 3 直角绝热边界附近布置单根冻结管 的情形 3.1 温度场解析解 在直角绝热边界附近布置单根冻结管,该冻结 管距热边界的距离分别 为d 和l,冻 结 管 中 心 沿y 方向到冻土边界的距离为ξ1,见图2. 在冻结管表面温度一定的情况下要直接求解稳 图2 直角绝热边界处单根冻结管示意图 Fig.2 Onefreezingpipeneararightangleadiabatic boundary 态温度场比较困难,为此,通过镜像法,以2个绝热 面为镜面分别找到单管的2个镜像,再找出1个平 衡像(这是为了使直角绝热面两直角边保持其绝热 性质),最终将单管冻结映射成以绝热边界为对称轴 的四管问题,然 后 通 过 势 函 数 叠 加 法 来 求 解,见 图 3.由对称性可知,在映射后四管的对称轴处,即原绝 热边界处,x、y 方向始终没有热 流 量,因 此,达 到 稳 态后,映射在上半平面第一象限内的单管温度场分 布与原问题等效. 图3中冻结管与3根镜像管中心的坐标分别为 P(l,d),J1(-l,d),J2(-l,-d)和J3(l,-d). 定义冻土边界条件点,其与冻结管中心 P 的连线与 第3期 胡向东,等:直角绝热边界附近少量冻结管稳态温度场解析解 374

474 浙江大学学报(工学版 第48老 A=In 8r。F+正 (6+2√合+4证√后+2)+4派】 将得出的1表达式代入式(10),并利用关系式:画= 品,=k8,和=k,最终组出直角绝热边界明 近布置单根冻结管时的稳态温度场的解析解为 a=a+5(a-a) (14) 式中 B-In L6(6+2)√合+4证√6+2a+4派 32解析解的数值模拟检哈 为了确认解析解推导过程的正确性及其简化处 3经镜像法映射成的四管示意医 Fig.3 Four pipes by mirror image method 理的合理性,采用成熟可靠的有限元数值计算进行 检验.本文采用ANSYS软件进行热学数值计算 y轴平行,该点坐标为(,d十) 模拟假定条件下的温度场分布,与解析解得到的结 设冻结管表面温度为,冻结管半径为r。,士 果进行对比.限于篇幅,本文仅以1-0.4m,d一Q5 体冻结温度为1,冻结管热流量为ga.根据势函数 m,台,=12m这种情祝为例来说明解析解准确性的 叠加原理,图3中冻结风域内任意点M(工,v)的热 势为冻结管与 验证,冻结管表面温度和冻结管半径取工程中常用 3根镜像管单独作用时产生的热 值,即 -70℃(考虑液氮冻结),r=0.054m 势的叠加,其表达式为 土体冻结温度取0,=0℃.由解析解式(14)得到的 (+i+C.(10) 温度场分布图见图4:通过冻结管中心沿v轴上的 温度场分布与数值模拟对比结果见图5:通过冻结 式中:r1、r、r3和r4分别为任意点到冻结管P及镜 像管J1J2和J,的距离,其表达式分别为 n--+(y=d n=++(y-d n1=√r+)+(y+d)下 0。 r=x-)+(y+d 冻土边界条件点(l,d+点)的势为 =-装[ln合+lnV后+4F+ 图4解析法得到的温度场分布图 n后+2+4+lh(+2)]+C(11) Fig.4 Temperature field calculated by analytical formul 冻结管边缘上的边界条件点((一。,dD处的势为 =-3[In ro In (21-re)+ 1n4+(2-r)+D、++C(12) 由于%相对于d和1来说很小,对计算值的影 响也很小,可将式(12)简化为 a=-2[lnr,+ln(2)+ln(2a+下)+ 10m3 2.0 1n(2d)7+C (13) 图5 通过冻结管中心沿 轴方向的直线上温度场分 由式(11)与式(13)可以解得: 度值 以结 - Fig.5 line in y directio 其中 ugh freezing pipe cente 1004.2015chi Academic Jour al Electronic Publishing House rights e http://www.cnki.ne
图3 经镜像法映射成的四管示意图 Fig.3 Fourpipesbymirrorimagemethod y 轴平行,该点坐标为(l,d+ξ1). 设冻结管表面 温 度 为θf1,冻 结 管 半 径 为r0,土 体冻结温度为θ01,冻结管热流量为qc1.根据势函数 叠加原理,图3中冻结区域内任意点 M(x,y)的热 势Φ1 为冻结管与3根镜像管单独作用时产生的热 势的叠加,其表达式为 Φ1 =-qc1 2π(lnr1 +lnr2 +lnr3 +lnr4)+C .(10) 式中:r1、r2、r3 和r4 分别为任意点到冻结管 P 及镜 像管J1、J2 和J3 的距离,其表达式分别为 r1 = (x-l)2 槡 + (y-d)2 , r2 = (x+l)2 槡 + (y-d)2 , r3 = (x+l)2 槡 + (y+d)2 , r4 = (x-l)2 槡 + (y+d)2 . 冻土边界条件点(l,d+ξ1)的势为 Φ01 =-qc1 2πlnξ1 +ln ξ 2 [ 槡1 +4l2 + ln (ξ1 +2d)2 槡 +4l2 +ln(ξ1 +2d)]+C. (11) 冻结管边缘上的边界条件点(l-r0,d)处的势为 Φf1 =-qc1 2π[lnr0 +ln(2l-r0)+ ln 4d2 槡 +(2l-r0)2 +ln 4d2 槡 +r2 0 ]+C.(12) 由于r0 相对于d和l来说很小,对计算值的影 响也很小,可将式(12)简化为 Φf1 =-qc1 2π[lnr0 +ln(2l)+ln(2 d2 槡 +l2 )+ ln(2d)]+C . (13) 由式(11)与式(13)可以解得: -qc1 2π=Φf1 -Φ01 A , 其中: A =ln 8dlr0 d2 槡 +l2 ξ1(ξ1 +2d) ξ 2 槡1 +4l2 (ξ1 +2d)2 [ ] 槡 +4l2 . 将得出的qc1表达式代入式(10),并利用关系式:Φ1= kθ1、Φ01=kθ01和Φf1=kθf1,最终得出直角绝热边界附 近布置单根冻结管时的稳态温度场θ1 的解析解为 θ1 =θ01 +B A(θf1 -θ01). (14) 式中: B =ln r1·r2·r3·r4 ξ1(ξ1 +2d) ξ 2 槡1 +4l2 (ξ1 +2d)2 [ ] 槡 +4l2 . 3.2 解析解的数值模拟检验 为了确认解析解推导过程的正确性及其简化处 理的合理性,采用成熟可靠的有限元数值计算进行 检验.本文采用 ANSYS软件进行热学数值计算来 模拟假定条件下的温度场分布,与解析解得到的结 果进行对比.限于篇幅,本文仅以l=0.4m,d=0.5 m,ξ1=1.2m 这种情况为例来说明解析解准确性的 验证.冻结管表面温度和冻结管半径取工程中常用 值,即θf1=-70 ℃ (考虑液氮冻结),r0=0.054m, 土体冻结温度取θ01=0 ℃.由解析解式(14)得到的 温度场分布图见 图4;通过冻结管中心沿y 轴 上 的 温度场分布与数值模拟对比结果见图5;通过冻 结 图4 解析法得到的温度场分布图 Fig.4 Temperaturefieldcalculatedbyanalyticalformula 图5 通过冻结管中心沿y轴方向的直线上温度场分布 与数值模拟结果对比 Fig.5 Comparisonofresultsofanalyticalformulaand numericalsimulationalonglineiny direction throughfreezingpipecenter 474 浙 江 大 学 学 报 (工学版) 第48卷
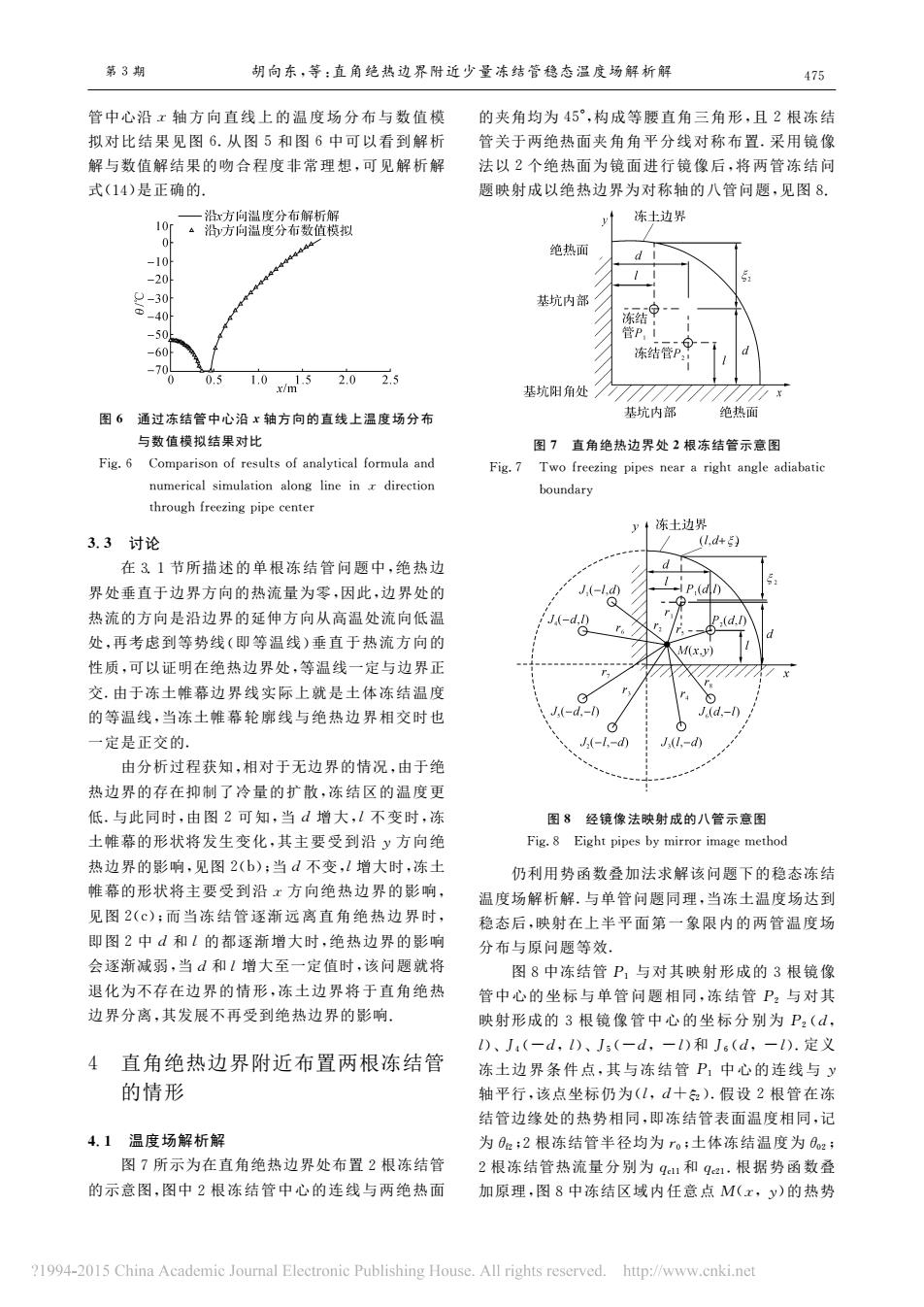
第3期 胡向东,等:直角绝热边界附近少量冻结管稳态温度场解析解 475 管中心沿x轴方向直线上的温度场分布与数值衫 的夹角均为45,构成等腰直角三角形,且2根连 拟对比结果见图6.从图5和图6中可以看到解析 管关于两绝热面夹角角平分线对称布置,采用镜像 解与数值解结果的吻合程度非常理想,可见解析解 法以2个绝热面为镜面进行镜像后,将两管冻结问 式(14)是正确的 题映射成以绝热边界为对称轴的八管间题,见图8 冻土边界 绝热面 8-30 基坑内部 05 10m2025 基坑用角处 围6通过冻结管中心沿x轴方向的直线上温度场分布 绝热面 与数值模拟结果对比 图7直角绝热边界处2根冻结管示意困 Fig.6 Comparison of results of analytical formula and Fig.7 Two freezing pipes near a right angle adiabatic numerical simulation along line in r direction boundary through freezing pipe cente 冻土边架 3.3讨论 ,d+) 在31节所描述的单根冻结管问题中,绝热边 界处垂直于边界方向的热流量为零,因此,边界处的 热流的方向是沿边界的延伸方向从高温处流向低 J-d3 处,再考虑到等势线(即等温线)垂直于热流方向 性质,可以证明在绝热边界处,等温线一定与边界正 交由于冻土帷幕边界线实际上就是士体冻结温度 的等温线,当冻土椎幕轮廓线与绝热边界相交时也 jxd-n 一定是正交的。 、4- J.(d,-d) 由分析过程获知,相对于无边界的情况,由于绝 热边界的存在抑制了冷量的扩散,冻结区的温度更 低.与此同时,由图2可知,当d增大,1不变时,冻 图8经镜像法映射成的八管示意图 土帷幕的形状将发生变化,其主要受到沿y方向绝 Fig.8 Eight pipes by mirror image method 热边界的影响,见图2(b):当d不变,1增大时,陈士 仍利用势函数叠加法求解该问题下的稳态冻结 帷幕的形状将主要受到沿x方向绝热边界的影响, 温度场解析解,与单管问恩同理,当冻土温度场达到 见图2(©):而当冻结管逐渐远离直角绝热边界时 稳态后,映射在上半平面第一象限内的两管温度场 即图2中d和的都逐渐增大时,绝热边界的影响 分布与原问题等效 会逐渐减弱,当d和【增大至一定值时,该间题就将 图8中冻结管,与对其映射形成的3根镜修 退化为不存在边界的情形,冻土边界将于直角绝热 管中心的坐标与单管问邀相同,冻结管P:与对其 边界分离,其发展不再受到绝热边界的影响 映射形成的3根镜像管中心的坐标分别为P,(d )、1(一d,l)、1(一d,一1)和。d,一).定义 4直角绝热边界附近布置两根冻结管 冻土边界条件点,其与冻结管P,中心的连线与 的情形 轴平行,该点坐标仍为(1,d+京).假设2根管在鸿 结管边缘处的热势相同,即冻结管表面温度相同,记 4.1温度场解析解 为e:2根冻结管半径均为ro:土体冻结温度为8a: 图7所示为在直角绝热边界处布置2根冻结管 2根冻结管热流量分别为,和,根据势函数叠 的示意图,图中2根冻结管中心的连线与两绝热面 加原理,图8中冻结区域内任意点M(x,y)的热势 994-2015 China Academic Joumal Electronic Publishing House.All rights reserved.http://www.cnki.ne
管中心沿x 轴 方 向 直 线 上 的 温 度 场 分 布 与 数 值 模 拟对比结果见图6.从图5和图6中可以看到解 析 解与数值解结果的吻合程度非常理想,可见解析解 式(14)是正确的. 图6 通过冻结管中心沿x轴方向的直线上温度场分布 与数值模拟结果对比 Fig.6 Comparisonofresultsofanalyticalformulaand numericalsimulationalonglineinx direction throughfreezingpipecenter 3.3 讨论 在3.1节所描述的单根冻结管问题中,绝 热 边 界处垂直于边界方向的热流量为零,因此,边界处的 热流的方向是沿边界的延伸方向从高温处流向低温 处,再考虑到等势线(即等温线)垂直于热流方向的 性质,可以证明在绝热边界处,等温线一定与边界正 交.由于冻土帷幕边界线实际上就是土体冻结温度 的等温线,当冻土帷幕轮廓线与绝热边界相交时也 一定是正交的. 由分析过程获知,相对于无边界的情况,由于绝 热边界的存在抑制了冷量的扩散,冻结区的温度更 低.与此同时,由 图2可 知,当d 增 大,l不 变 时,冻 土帷幕的形状将发生变化,其主要受到沿y 方向绝 热边界的影响,见图2(b);当d不变,l增大时,冻土 帷幕的形状将主要受到沿x 方向绝热边界的影响, 见图2(c);而当冻结管逐渐远离直角绝热边界时, 即图2中d 和l的都逐渐增大时,绝热边界的影响 会逐渐减弱,当d和l增大至一定值时,该问题就将 退化为不存在边界的情形,冻土边界将于直角绝热 边界分离,其发展不再受到绝热边界的影响. 4 直角绝热边界附近布置两根冻结管 的情形 4.1 温度场解析解 图7所示为在直角绝热边界处布置2根冻结管 的示意图,图中2根冻结管中心的连线与两绝热面 的夹角均为45°,构成等腰直角三角形,且2根冻结 管关于两绝热面夹角角平分线对称布置.采用镜像 法以2个绝热面为镜面进行镜像后,将两管冻结问 题映射成以绝热边界为对称轴的八管问题,见图8. 图7 直角绝热边界处2根冻结管示意图 Fig.7 Twofreezingpipesneararightangleadiabatic boundary 图8 经镜像法映射成的八管示意图 Fig.8 Eightpipesbymirrorimagemethod 仍利用势函数叠加法求解该问题下的稳态冻结 温度场解析解.与单管问题同理,当冻土温度场达到 稳态后,映射在上半平面第一象限内的两管温度场 分布与原问题等效. 图8中冻结管P1 与对其映射形成的3根镜像 管中心的坐标与单管问题相同,冻 结 管 P2 与 对 其 映射形成的3根 镜 像 管 中 心 的 坐 标 分 别 为 P2 (d, l)、J4(-d,l)、J5(-d,-l)和J6(d,-l).定义 冻土边 界 条 件 点,其 与 冻 结 管 P1 中 心 的 连 线 与y 轴平行,该点坐标仍为(l,d+ξ2).假设2根管在冻 结管边缘处的热势相同,即冻结管表面温度相同,记 为θf2;2根冻结管半径均为r0;土体冻结温度为θ02; 2根冻结管热流量分别为qc11和qc21.根据势函数叠 加原理,图8中冻结区域内任意点 M(x,y)的热势 第3期 胡向东,等:直角绝热边界附近少量冻结管稳态温度场解析解 574

476 浙江大学学报(工学版) 第48卷 少:为冻结管P、P:与镜像管1一J。单独作用时产 生的热势的叠加,其表达式为 =-·ln(8dlr。V+)- ln(2(d-0(d+)[(d+D2+ =-驶(nn+ln十lnn十ln)- (d-2]}+c (19) (++)+C. (15) a=-婴ln2d-Dd+[d-+ 式中:。和,分别为任意点到冻结管P:及 镜像管J:、J和J。的距离,其表达式分别为 (d+I()+C. n=√x-d0+(y-) (20) 根据之前假定,2根冻结管边缘处的热势相同, -√r+d)+(y-D 即Φ,=Φ1,将两者记为Φ,:由式(19)与式(20)可 n,=√x+d)+(y+ 得9am=ga,将两者记为9a.将式(15)、(16)、(19) =-D++ 和(20)统一用q2表示为 冻土边界条件点(化,d+)的势为 =-2n(m·n·nn%nn·)+C, nA-2nB+C (16) (21) 式中: (22) A1-(+2d)√+4√+2)+4 电=-In(A,B,)+C, B=B·B·Ba·B Pa:-Per -D:--In (A:B:)+C. (23) B-√+d-D+(d- 式中: B,=(6+d-)2+(d+)F A:=8dlro+ B-√6+d+D2+(d+ B.=2(d-1)(d+1)「(d+)2+(d-1)2] B-√a+d+)2+(d- 由式(22)与式(23)可以解得: 2根冻结管边缘上的边界条件点(1一。,d)和 (d一,D处的势和分别为 -装=nA:B/AB万 :=-[n+lh21-w)+ 将得出的g表达式代入式(21),并利用关系式:虫= ,=:和4e=,最终得出直角绝热边界附 ln√A+(2l-rF+ln√4d+r] 近布置2根冻结管时的稳态温度场(解析解为 a2=0e+ [n√d-l++(d-+ In [(r ln/(d+I-r。)2+(d-l)+ (AA) n√d+1-)+(d++ (24) ln√d-1+)+(d+)厅]+C, 解析解的数值模拟检验 (17) 同样采用ANSYS软件进行热学数值计算来模 Φ=-[lnvd-l-r)+(d-+ 拟假定条件下的温度场分布,与解析解得到的结果进 行对比来检验该解析公式的准确性.以1=Q5m,d= In (d+1-ro(d-D+ 10m,=12m情况为例.冻结管表面温度、冻结管 n√d+1-)+d++ 半径与土体冻结温度的取值与单管问题中相同.由解 ln√d-1-o)+(d+] 析解式(24)得到的温度场分布图见图9:通过冻结管 婴[ln+lh(2d-)+ P:中心沿y轴上的温度场分布与数值模拟对比结果 见图10:通过冻结管卫中心沿y轴上的温度场分布 ln√2d-o)+4F+ln√4r+]+C 与数值模拟对比结果见图11.从图中可以看到解积 (18 解与数值解结果吻合同样较好,解析解正确.此外 由于。相对于d和1来说相对很小,对计算值 与单根冻结管的情况类似,冻土轮喘线与绝热边界 的影响也很小,因此,可将式(17)和式(18)简化为 正交,且随着d和1的增大,绝热边界对温度场产生 1994-2015 China Aeademic Joumal Eleetronic Publishing House.All rights reserved http://www.cnki.ne
Φ2 为冻结管P1、P2 与镜像管J1~J6 单独作用时产 生的热势的叠加,其表达式为 Φ2 =-qc11 2π(lnr1 +lnr2 +lnr3 +lnr4)- qc21 2π(lnr5 +lnr6 +lnr7 +lnr8)+C . (15) 式中:r5、r6、r7 和r8 分 别 为 任 意 点 到 冻 结 管 P2 及 镜像管J4、J5 和J6 的距离,其表达式分别为 r5 = (x-d)2 槡 + (y-l)2 , r6 = (x+d)2 槡 + (y-l)2 , r7 = (x+d)2 槡 + (y+l)2 , r8 = (x-d)2 槡 + (y+l)2 . 冻土边界条件点(l,d+ξ2)的势为 Φ02 =-qc11 2π lnA1 -qc21 2π lnB1 +C . (16) 式中: A1 =ξ2(ξ2 +2d) ξ 2 槡2 +4l2 (ξ2 +2d)2 槡 +4l2 , B1 =B11·B12·B13·B14, B11 = (ξ2 +d-l)2 槡 + (d-l)2 , B12 = (ξ2 +d-l)2 槡 + (d+l)2 , B13 = (ξ2 +d+l)2 槡 + (d+l)2 , B14 = (ξ2 +d+l)2 槡 + (d-l)2 . 2根冻结管边缘上的边界条 件 点(l-r0,d)和 (d-r0,l)处的势Φf11和Φf21分别为 Φf11 =-qc11 2π[lnr0 +ln(2l-r0)+ ln 4d2 槡 + (2l-r0)2 +ln 4d2 槡 +r2 0 ]- qc21 2π ln (d-l+r0)2 [ 槡 + (d-l)2 + ln (d+l-r0)2 槡 + (d-l)2 + ln (d+l-r0)2 槡 + (d+l)2 + ln (d-l+r0)2 槡 + (d+l)2 ]+C, (17) Φf21 =-qc11 2π ln (d-l-r0)2 [ 槡 + (d-l)2 + ln (d+l-r0)2 槡 + (d-l)2 + ln (d+l-r0)2 槡 + (d+l)2 + ln (d-l-r0)2 槡 + (d+l)2 ]- qc21 2π[lnr0 +ln(2d-r0)+ ln (2d-r0)2 槡 +4l2 +ln 4l2 槡 +r2 0 ]+C. (18) 由于r0 相对于d和l来说相对很小,对计算值 的影响也很小,因此,可将式(17)和式(18)简化为 Φf11 = -qc11 2π·ln(8dlr0 d2 槡 +l2 )-qc21 2π· ln{2(d-l)(d+l)[(d+l)2 + (d-l)2]}+C, (19) Φf21 = -qc11 2π ln{2(d-l)(d+l)[(d-l)2 + (d+l)2]}-qc21 2π ln(8dlr0 d2 槡 +l2 )+C. (20) 根据之前假定,2根冻结管边缘处的热势相同, 即Φf11=Φf21,将两者记为Φf2;由式(19)与式(20)可 得qc11=qc21,将两者记为qc2.将式(15)、(16)、(19) 和(20)统一用qc2表示为 Φ2 =-qc2 2π ln(r1·r2·r3·r4·r5·r6·r7·r8)+C, (21) Φ02 =-qc2 2π ln(A1B1)+C , (22) Φf11 =Φf21 =Φf2 =-qc2 2π ln(A2B2)+C . (23) 式中: A2 =8dlr0 d2 槡 +l2 , B2 =2(d-l)(d+l)[(d+l)2 + (d-l)2]. 由式(22)与式(23)可以解得: -qc2 2π= Φf2 -Φ02 ln(A2B2/(A1B1)), 将得出的qc2表达式代入式(21),并利用关系式:Φ2= kθ2、Φ02=kθ02和Φf2=kθf2,最终得出直角绝热边界附 近布置2根冻结管时的稳态温度场θ2 解析解为 θ2 =θ02 + ln [(r1·r2·r3·r4·r5·r6·r7·r8)/(A1B1)] ln[A2B2/(A1B1)] · (θf2 -θ02). (24) 4.2 解析解的数值模拟检验 同样采用 ANSYS软件进行热学数值计算来模 拟假定条件下的温度场分布,与解析解得到的结果进 行对比来检验该解析公式的准确性.以l=0.5m,d= 1.0m,ξ2=1.2m情况为例.冻结管表面温度、冻结管 半径与土体冻结温度的取值与单管问题中相同.由解 析解式(24)得到的温度场分布图见图9;通过冻结管 P1 中心沿y轴上的温度场分布与数值模拟对比结果 见图10;通过冻结管P2 中心沿y轴上的温度场分布 与数值模拟对比结果见图11.从图中可以看到解析 解与数值解结果吻合同样较好,解析解正确.此外, 与单根冻结管的情况类似,冻土轮廓线与绝热边界 正交,且随着d和l的增大,绝热边界对温度场产生 674 浙 江 大 学 学 报 (工学版) 第48卷

第3期 胡向东,等:直角绝热边界附近少量冻结管稳态温度场解析解 477 点位置已知的稳态温度场问题来求解 (2)通过镜像法得到了原问题的映射问题,并基于 势函数叠加方法推导出了直角绝热边界附近布置单根 和两根冻结管时的稳态温度场分布解析解表达式: (3)通过对相同情况下的间题讲行数值模拟可 以得到已知问题的数值解,将两者的结果相对比,发 现吻合较好,可以推断该公式具有足够的精度,可为 05 工程中出现的类似问题提供一定的理论指导, 参考文献(References): 图9解析法得到的温度场分布图 Fig.Temperature field calculated by analytical formula ·然阁疆度分布餐 TRUPAK N G.Grou [2]BAXOJIIIHH BB.BGoD -30 BAKHOLDIN B V.Selection of optimized mode of 03 0 Wm2025 ground freezing for construction purpose [MJ.Moscow. State Construction Press,1963.(in Russian) [3]SANGER F J.SAYLES F H.Thermal and rheologica 图10通过冻结管卫中心沿y轴方向的直线上温度场 omputations for artilicially frozen ground constructior 分布与数值模拟结果对比 Fig.10 Comparison of results of analytical formula and ,1979.13(-4):311-337 numerical simulation along line in y direction 部幅秋元攻 上内温度分布計算式上,)店用 through center of freezing pipe P. 5(8):-1 19·方胸隆分充新部 979.548),3-1 [5]加藤哲治,伊豆久雄,指田幸弘.温度分布任 の曲跑)解析上演土設计平均温度评缅法考察 -30 11+学04作E.2007.63111.02-10 KATO T.IZUTA H.KUSHIDA Y Bending strength of frozen soil beam with temrerature distribution and oonsider tion of average temperature evaluation method ]]Dobok 10m202 Gakkal Ronbunshuu F.2007.63(1).97-106. 图11通过冻结首B中心沿y轴方向的直线上温度场 [6]陈文豹,汤老斌。潘集矿区冻结壁平均温度及冻结孔布 置圈径的探讨[U门.煤炭学报.1982,7(1):46-52 分布与散值模拟结果对比 CHEN Wen-bao.TANG Zhi-bin.The average tempera Fig.11 Comparison of results of analytical formula and ture in ice wall and the diameter of frozen circle in Pan numerical simulation along line in y direction Coal Field [J].Journal of China Coal Society.1982.7 through center of freezing pipe P: 的影响将逐渐减小,冻土推幕形状也将产生类似变 化,不再赘述. 5结论 nd sei (1)通过对实际工程问题的抽象,提出了直角 New York:American 绝热边界附近布置少量冻结管,并通过引入温度场 Institute of Physics.2009:1333-1338. 下转第547页) 为稳态等假设,将问题简化成冻土帷幕边界上某 1994-2015 China Academic Joumal Electronic Publishing House.All rights reserved.htp://www.cnkin
图9 解析法得到的温度场分布图 Fig.9 Temperaturefieldcalculatedbyanalyticalformula 图10 通过冻结管P1 中心沿y轴方向的直线上温度场 分布与数值模拟结果对比 Fig.10 Comparisonofresultsofanalyticalformulaand numericalsimulationalonglineiny direction throughcenteroffreezingpipeP1 图11 通过冻结管P2 中心沿y轴方向的直线上温度场 分布与数值模拟结果对比 Fig.11 Comparisonofresultsofanalyticalformulaand numericalsimulationalonglineiny direction throughcenteroffreezingpipeP2 的影响将逐渐减小,冻土帷幕形状也将产生类似变 化,不再赘述. 5 结 论 (1)通过对 实 际 工 程 问 题 的 抽 象,提 出 了 直 角 绝热边界附近布置少量冻结管,并通过引入温度场 为稳态等假设,将问题简化成冻土帷幕边界上某一 点位置已知的稳态温度场问题来求解; (2)通过镜像法得到了原问题的映射问题,并基于 势函数叠加方法推导出了直角绝热边界附近布置单根 和两根冻结管时的稳态温度场分布解析解表达式; (3)通过对相同情况下的问题进行数值模拟可 以得到已知问题的数值解,将两者的结果相对比,发 现吻合较好,可以推断该公式具有足够的精度,可为 工程中出现的类似问题提供一定的理论指导. 参考文献(References): [1]ТРУПАК НГ. Замораживание горных пород при проходкестволов[M].Москва:Углетехиздат,1954. TRUPAK N G.Groundfreezinginshaftsinking[M]. Moscow:CoalTechnologyPress,1954.(inRussian) [2]БАХОЛДИНБВ. Выбор оптимального режима замораживаниягрунтов в строительных целях[M]. Москва:Госстройиздат,1963. BAKHOLDIN B V.Selection of optimized mode of groundfreezingforconstructionpurpose[M].Moscow. StateConstructionPress,1963.(inRussian) [3]SANGERFJ,SAYLESF H.Thermalandrheological computationsforartificiallyfrozengroundconstruction [J].EngineeringGeology,1979,13(1-4):311-337. [4]戸部 暢,秋元 攻.凍土内温度分布計算式と,その応用 [J].冷凍,1979,54(8):3-11. TOBEN,AKIMOTOO.Temperaturedistributionfor- mulainfrozensoilanditsapplication[J].Refrigeration, 1979,54(8):3-11. [5]加藤 哲治,伊豆田 久雄,櫛田 幸弘.温度分布凍土ばり の曲げ強さ の解 析と凍土設計平均温度評価法の考 察 [J].土木学会論文集 F,2007,63(1):97-106. KATO T,IZUTA H,KUSHIDAY.Bendingstrengthof frozensoilbeamwithtemperaturedistributionandconsider- ationofaveragetemperatureevaluationmethod[J].Doboku GakkaiRonbunshuuF,2007,63(1):97-106. [6]陈文豹,汤志斌.潘集矿区冻结壁平均温度及冻结孔布 置圈径的探讨[J].煤炭学报,1982,7(1):46-52. CHEN Wen-bao,TANGZhi-bin.Theaveragetempera- tureinicewallandthediameteroffrozencircleinPanji CoalField[J].JournalofChinaCoalSociety,1982,7 (1):46-52. [7]HU Xiang-dong.AverageTemperature modelofdouble- row-pipefrozensoilwallbyequivalenttrapezoid method [C]∥ ProceedingsoftheSecondInternationalSymposiumon ComputationalMechanicsandtheTwelfthInternationalCon- ferenceontheEnhancementandPromotionofComputational MethodsinEngineeringandScience.New York:American InstituteofPhysics,2009:1333-1338. (下转第547页) 第3期 胡向东,等:直角绝热边界附近少量冻结管稳态温度场解析解 774

第3期 向甜,等:三轴磁张计与MEMS陀螺的在轨实时标定方法 547 ce and Exhibit.Providence [10]SIMON I.IEFFREY U.HUGH F D W.A new Rhode Island sn 1 2004.1-11 nethod for the nonlinea [8)]秦伟,苑伟政,常洪龙,等,基于自适应UKF算法的 ovariances in filters and estimators[IEEE Trans MEMS陀螺空中在线标定技术].中国惯性技术学报, stion on Automatie Control.2000.4503)477-482 9011.1023.170174 [11]CRASSIDIS I L,MARKLEY F L.Unscented filtering OIN Wai YUAN WeL for sna ecraft attitude estimation Journal of Guid ance Control and Dynamics 2003 2644)536-542 ted kalman filter algo 「12】张锐,朱振才,张静,等.基于磁强计的微小卫星姿态确 定下1门立航受报.20062714).578-581 1091.170-174 ZHANG Rui.ZHU Zhen-cai.ZHANG Jing,et al. [9]CRASSIDIS IL.Sigma-Point Kalman Filtering for inte attitude determination hased on magne grated ges and inertial navigationtCl/alaa guidance tometer [1]Journal of Astronautics.2006.27(4) Navigation.and Control Conference and Exhibit.San 57-581 Francisco.California AlAA.2005.750-756. (上接第477页】 [8胡向东,黄蜂,白楠。考虑土层冻结温度时人工冻结温 tion in single-tow freezing [J]Journal of China 度场榄型[.中国矿业大学学报, 2008,37(4 Coal Societv.2011.36(8):938-914. 「12胡向东,拟本 人工冻结温度场巴霍尔金模型准确性研 HU Xiang-dong.HUANG Feng.BAI Nan.Models of 究0地下空与工程学报.2010.61):96-101. ing point Jourml of China University of Mining& T 2008.374).550-555 lournal of Und [9]胡向东,白楠,余锋.单排管冻结温度场TPYIIAK和 mg,2010.61),96-10L 5AXO,IHH公式的适用性[J].同济大学学报:自然 [13]胡向东。直线形单排管冻土意平均温度计算方法 学版,2008,36(7).906-910 [J.冰川冻土,2010.32(40:778-785. HU Xia BAI Nan.YU Feng.Analysis of Tru HU Xiar ation for th pak and Bakholdin fo raight sing mal of Tongii Uni d 2010.3241.77785 .001a [1们胡向东,赵飞,余思源, ,白线双排管结壁平均 「10胡向东,挺秀,多挂管直提冻土墙平均温度的等效 度的等效抛物号形模型[].煤炭学报,2012,37(1): 梯形计算方法[J].煤炭学报,2009,3411):146 140 ng.ZHAO Fei.SHE S-yuan HU Xiane-dong.HE Ting-xiu Eauivalent nethod of ow-Dipe Coal Society.2012.371:28-32. .2009.34111.1465-1469 [1门胡传鹏,胡向东,朱合华。单排管冻结巴蛋尔金温度 0们岩石力学与工程 场控制参数敏感度分析「门棋炭学报, 2011,36(8) HU Xiang-dong.WANG Y ng.Analytical solution of 038-944 field by mea of eakboldin solu in 2012.31(5).1071-1080 1994-2015 China Academie Joumal Electronic Publishing House.All rights reserved http://www.cnki.ne
dyna-micsSpecialistConferenceandExhibit.Providence. RhodeIsland:[s.n.],2004:1-11. [8]秦 伟,苑 伟 政,常 洪 龙,等.基 于 自 适 应 UKF 算 法 的 MEMS陀螺空中在线标定技术[J].中国惯性技术学报, 2011,19(2):170-174. QIN Wei,YUAN Wei-zheng,CHANG Hong-long,et al.In-flighton-linecalibrationmethodforMEMSgyro- scopebasedonadaptiveunscented Kalmanfilteralgo- rithm[J].JournalofChineseInertialTechnology,2011, 19(2):170-174. [9]CRASSIDISJL.Sigma-PointKalmanFilteringforinte- gratedGPSandinertialnavigation[C]∥AIAAGuidance, Navigation,and Control Conference and Exhibit.San Francisco,California:AIAA,2005:750-756. [10]SIMON J,JEFFREY U,HUGH F D W.A new methodforthenonlineartransformationofmeansand covariancesinfiltersandestimators[J].IEEETrans- actiononAutomaticControl,2000,45(3):477-482. [11]CRASSIDISJL,MARKLEYFL.Unscentedfiltering forspacecraftattitudeestimation[J].JournalofGuid- ance,ControlandDynamics,2003,26(4):536-542. [12]张锐,朱振才,张静,等.基于磁强计的微小卫星姿态确 定 [J].宇航学报,2006,27(4):578-581. ZHANG Rui,ZHU Zhen-cai,ZHANG Jing,etal. Micro-satelliteattitudedeterminationbasedonmagne- tometer[J].JournalofAstronautics,2006,27(4): 檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾檾 578-581. (上接第477页) [8]胡向东,黄峰,白楠.考虑土层冻结温度时人工冻结温 度 场 模 型 [J].中国矿业大学学报,2008,37(4): 550-555. HU Xiang-dong,HUANGFeng,BAINan.Modelsof artificialfrozentemperaturefieldconsideringsoilfreez- ingpoint[J].JournalofChinaUniversityofMining & Technology,2008,37(4):550-555. [9]胡向东,白楠,余 锋.单排管冻结温度场 ТРУПАК 和 БАХОЛДИН 公式的 适 用 性[J].同 济 大 学 学 报:自 然 科学版,2008,36(7):906-910. HU Xiang-dong,BAINan,YUFeng.AnalysisofTru- pakandBakholdinformulasfortemperaturefieldofsin- gle-row-pipefrozensoilwall[J].JournalofTongjiUni- versity:NaturalScience,2008,36(7):906-910. [10]胡向东,何挺秀.多排管直线冻土墙平均温度的等效 梯形计 算 方 法 [J].煤 炭 学 报,2009,34(11):1465- 1469. HU Xiang-dong,HE Ting-xiu.Equivalent-trapezoid methodofaveragetemperaturecalculationfor multi- row-pipestraightfrozensoilwall[J].JournalofChina CoalSociety,2009,34(11):1465-1469. [11]胡传鹏,胡 向 东,朱 合 华.单排管冻结巴霍尔金温度 场控制参数敏感度分析[J].煤 炭 学 报,2011,36(8): 938-944. HuChuan-peng,HuXiang-dong,ZhuHe-hua.Sensi- tivityanalysisofcontrolparametersofBakholdinsolu- tioninsingle-row-pipefreezing [J].JournalofChina CoalSociety,2011,36(8):938-944. [12]胡向东,赵俊杰.人工冻结温度场巴霍尔金模型准确性研 究[J].地下空间与工程学报,2010,6(1):96-101. HUXiang-dong,ZHAOJun-jie.Researchonprecision ofBakholdin modelfortemperaturefieldofartificial groundfreezing[J].ChineseJournalof Underground SpaceandEngineering,2010,6(1):96-101. [13]胡向 东.直线形单排管冻土帷幕平均温度计算方法 [J].冰川冻土,2010,32(4):778-785. HUXiang-dong.Averagetemperaturecalculationforthe straightsingle-row-pipefrozensoilwall[J].Journalof GlaciologyandGeocryology,2010,32(4):778-785. [14]胡向东,赵飞,佘思源,等.直线双排管冻结壁平均温 度的等效抛物弓形模型[J].煤 炭 学 报,2012,37(1): 28-32. HU Xiang-dong,ZHAO Fei,SHE Si-yuan,et al. Equivalentparabolicarch methodofaveragetemperature calculationforstraightdouble-row- pipefrozensoilwall [J].JournalofChinaCoalSociety,2012,37(1):28-32. [15]胡向东,汪洋.三排管冻结温度场的势函数叠加法解析解 [J].岩石力学与工程学报,2012,31(5):1071-1080. HU Xiang-dong,WANG Yang.Analyticalsolutionof three-row-pipedfrozentemperaturefieldby meansof superpositionofpotential[J].ChineseJournalofRock MechanicsandEngineering,2012,31(5):1071-1080. 第3期 向甜,等:三轴磁强计与 MEMS陀螺的在轨实时标定方法 745